Hieronder in dit artikel vindt u verschillende opgeloste percentageproblemen , die alle moeilijkheidsgraden bestrijken. Bovendien bestrijken ze een breed scala aan onderwerpen die doorgaans worden bestudeerd met behulp van percentages . Dat gezegd zijnde raden wij u aan om de problemen zelf op te lossen en als u klaar bent, uw resultaten te vergelijken met de resultaten die wij u in dezelfde oefeningen aanbieden. Voordat we met de activiteiten beginnen, zullen we echter eerst wat praten over de beste methoden die er zijn om problemen met percentages op te lossen.
Hoe problemen met percentages oplossen?
Om een percentageprobleem op te lossen, raden we aan de basisoplosprocedure voor rekenproblemen te volgen. In deze laatste link leggen we in detail uit wat de te volgen stappen zijn, hoewel we hieronder een samenvatting zullen maken gericht op het oplossen van de percentages:
- Het probleem begrijpen: in deze eerste fase van de oplossing zullen we het probleem moeten classificeren op basis van het soort percentage dat het ons laat berekenen. De belangrijkste soorten zijn onder meer: BTW, verhogingspercentages, verlagingspercentages, gelijkwaardigheidspercentages.
- Maak een diagram: Zodra we duidelijk weten met welk type probleem we worden geconfronteerd, moeten we doorgaan met het in kaart brengen van het doel en de gegevens van de oefening. Als u echter niet wilt tekenen, kunt u altijd een diagram schrijven met de gegevens die bij de berekeningen betrokken zijn en deze aan elkaar relateren.
- Begin met de berekeningen: later kunnen we beginnen met het wiskundig oplossen van de oefening, dit deel is eenvoudig als je de oefening in de vorige secties correct hebt opgesteld. Sindsdien weet u op elk moment heel duidelijk wat u moet doen om het resultaat te bereiken.
- Conclusies: ten slotte moeten we het resultaat uitdrukken, dit kan in een zin zijn of eenvoudigweg in de numerieke waarde waarnaar ons wordt gevraagd. En het wordt ten zeerste aanbevolen dat we, als we klaar zijn met het probleem, het van begin tot eind analyseren en conclusies trekken.
Percentage problemen voor alle niveaus
Nu we hebben uitgelegd hoe je oefeningen met percentages oplost, kun je gaan oefenen met enkele oefeningen. In de volgende lijst vind je problemen voor alle leerjaren , van oefeningen voor degenen die met percentages beginnen te werken, tot enkele behoorlijk ingewikkelde. Zelfs als je het niveau hebt dat je hebt, raden we je aan om met de gemakkelijkste te beginnen (de eerste) en zo ver mogelijk omhoog te gaan.
eerste probleem
Op één school zijn er 240 leerlingen, van wie er 160 alle vakken hebben gehaald. Hoeveel procent van de studenten slaagde voor alle vakken?
We hebben 160 van de 240 studenten die alle vakken hebben behaald, dus 240 is gelijk aan 100% en 160 is gelijk aan x%. Om erachter te komen hoeveel x waard is, volgen we een eenvoudige regel van drie :
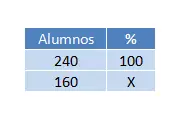
Daarom is het resultaat van de bewerking (160 x 100) ÷ 240 = 66,67%, of tweederde van het totaal. Dus als we de oplossing in een zin willen uitdrukken, kunnen we dat aangeven met het percentage (dat vragen ze ons in de verklaring) of we kunnen het doen met de verhouding.
tweede probleem
Op een parkeerplaats staan 150 auto’s, waarvan 50% wit, 30% rood en de rest blauw. Hoeveel auto’s zijn er van elke kleur?
We hebben in totaal 150 auto’s en we moeten ze indelen in 3 verschillende groepen op basis van verfkleur. We moeten daarom net als voorheen drie berekeningen maken:
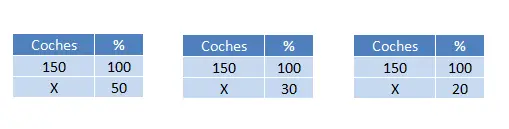
Daarom krijgen we drie waarden: (50 x 150) 100 = 75 auto’s, (30 x 150) 100 = 45 auto’s en (20 x 150) 100 = 30 auto’s. Ten slotte kunnen we, om te controleren of deze resultaten kloppen, ze allemaal bij elkaar optellen en dat zou ons 150 moeten opleveren, want dat is het totaal. Deze berekening maakt geen deel meer uit van de oefening, maar dient ter controle: 75 + 45 + 30 = 150 auto’s.
derde probleem
Als we een televisie willen kopen die €800 kost en ze bieden ons een korting van 15%, hoeveel moeten we dan uiteindelijk voor de televisie betalen?
Wij hanteren een totaalprijs van € 800,-, deze wordt verlaagd met 15% (dit is een kortingspercentage). We hoeven dus slechts één regel van drie op te lossen:
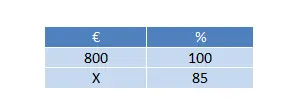
In dit geval is het noodzakelijk om de waarde te berekenen die overeenkomt met een kortingspercentage (100% – 15%) = 85%. De uiteindelijke berekening blijft dus als volgt: (85 x 800) ÷ 100 = €680.
vierde probleem
We hadden 250 liter opgeslagen in een watertank, op de eerste dag was dit watervolume teruggebracht tot 75% van de totale capaciteit. En de volgende dag werd de resterende capaciteit met 15% verminderd. Hoeveel kubieke meter zit er aan het eind van de tweede dag nog in de tank?
Om dit probleem op te lossen, moeten we twee hoeveelheden berekenen in de volgorde die in de verklaring is vastgelegd. Wij berekenen eerst 75% van 250, daarna 85% (100% – 15%) van het resterende bedrag.
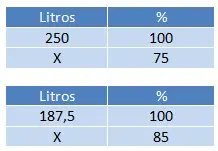
Om de resterende hoeveelheid van de eerste dag te verkrijgen, lossen we op voor (75 x 250) ÷ 100 = 187,5 liter water en dan doen we (85 x 187,5) ÷ 100 = 159,375 liter water.
vijfde probleem
Als ik op twee artikelen 21% BTW moet betalen, één van € 135 en de andere van € 56, maar het tweede product profiteert van 12% korting. Hoeveel moet ik uiteindelijk betalen voor de aankoop van beide artikelen?
Bij dit probleem zijn verschillende berekeningen betrokken: we beginnen met het berekenen van de uiteindelijke prijs van het tweede product (na de korting), daarna berekenen we de prijs van de twee producten inclusief BTW en tot slot tellen we de twee prijzen bij elkaar op.
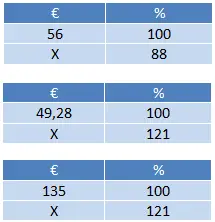
De prijs van het tweede product als we de korting toepassen is (88 x 56) ÷ 100 = € 49,28, dan passen we BTW toe op beide producten: (121 x 49,28) ÷ 100 = € 59,63 en (121 x 135) ÷ 100 = € 163,35. Ten slotte hoeven we alleen maar op te tellen tot 59,63 + 163,35 = € 222,98.
laatste oefening
Bereken de volgende percentages:
- 25% van 540 = 135
- 32% van 160 = 51,2
- 46% van 625 = 287,5
- 73% van 873 = 637,29
Als u deze oefeningen heeft voltooid en meer problemen met betrekking tot percentages wilt, raden wij u aan deze link te gebruiken. Daar vindt u procentuele problemen in pdf, deze verschillen niet veel van de problemen die we in dit artikel hebben genoemd en ze zullen u in staat stellen het concept van percentages te internaliseren.