▷ Hoe bereken je het middelpunt van een segment? (formule)

Op deze pagina wordt de betekenis van het middelpunt van een segment uitgelegd. Bovendien ontdekt u hoe u het midden van een segment kunt vinden met behulp van de formule. U zult zelfs voorbeelden, oefeningen en opgeloste problemen van segmentmiddenpunten zien.

Wat is het middelpunt van een segment?

In de wiskunde is het middelpunt van een segment het punt dat zich op dezelfde afstand van de eindpunten van een segment bevindt. Het midden verdeelt het segment dus in twee gelijke delen.

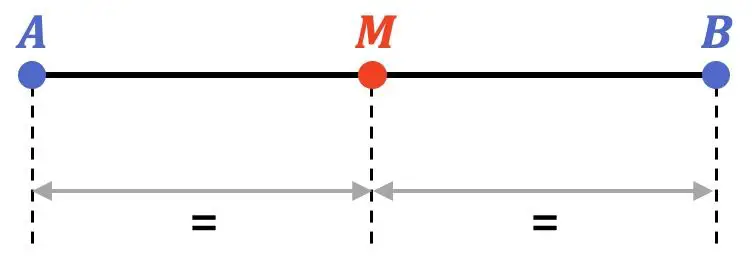
definitie van het midden van een segment

Bovendien ligt het middelpunt precies in het midden van het segment en behoort het dus tot de bissectrice van het segment.

Aan de andere kant is het middelpunt van een segment ook een punt op gelijke afstand van twee geometrische elementen: de twee uiteinden van het segment.

Hoe bereken je het middelpunt van een segment?

Gegeven de cartesiaanse coördinaten van de uiterste punten van een segment:

$A(x_1,y_1) \qquad B(x_2,y_2)$

De coördinaten van het midden van genoemd segment komen overeen met de halve som van de coördinaten van de uiterste punten:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

Dit is de formule voor het midden van een segment in het cartesiaanse vlak (in R2). Maar uiteraard is de formule ook van toepassing op de cartesiaanse ruimte (in R3), je hoeft alleen maar de halve som van de Z-coördinaat toe te voegen:

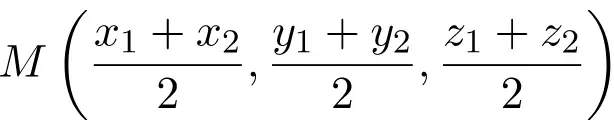
Laten we een voorbeeld bekijken van hoe u de coördinaten van het middelpunt van een segment kunt berekenen:

Bepaal het middelpunt van het segment dat wordt gevormd door de volgende punten:

$A(2,5) \qquad B(4,-1)$

Om het midden van het segment te vinden, past u eenvoudigweg de formule toe:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

Oefeningen opgelost in het midden van een segment

Oefening 1

Wat is het middelpunt van het segment waarvan de eindpunten de volgende twee punten zijn?

$A(3,-2) \qquad B(5,8)$

Zie de oplossing

Om het midden van het segment te vinden, moet u de formule rechtstreeks toepassen:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

Oefening 2

Zoek de coördinaten van het eindpunt van het segment dat begint bij punt A en waarvan het middelpunt M is.

$A(4,-1) \qquad M(-2,1)$

Zie de oplossing

In dit geval kennen we de coördinaten van het beginpunt en het midden van het segment. Daarom vervangen we de coördinaten die we kennen in de formule voor het middelpunt van een segment:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

En nu lossen we de coördinaten van het eindpunt van het segment uit de vorige vergelijking op:

X-coördinaten

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

Y-coördinaten

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

De coördinaten van het laatste uiteinde van het segment zijn daarom:

$\bm{B(-8,3)}$

Oefening 3

Gegeven het volgende parallellogram:

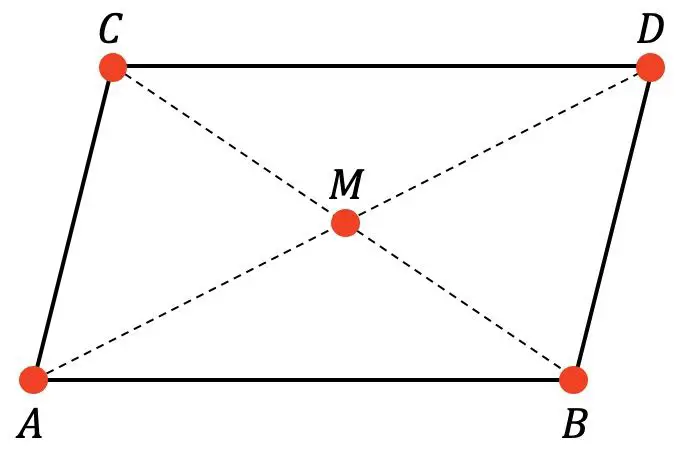
We weten dat M het middelpunt van het parallellogram is en dat de coördinaten van de punten A, B en C zijn:

$A(1,1) \quad B(5,1) \quad C(7,3)$

Bereken op basis van deze informatie en met behulp van de middelpuntformule de coördinaten van punt D.

Zie de oplossing

Om de coördinaten van punt D te vinden met behulp van de formule voor het midden van een lijnstuk, moet u eerst de coördinaten van punt M berekenen en vervolgens die van punt D.

Punt M is het middelpunt van segment BC, de coördinaten zijn daarom:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

En zodra we punt M kennen, kunnen we punt D vinden. Punt M ligt ook in het midden van segment AD, dus:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

X-coördinaat van punt D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

Y-coördinaat van punt D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

De coördinaten van punt D zijn dus:

$\bm{D(11,3}$

Oefening 4

Bereken de continue vergelijking van de lijn loodrecht op het segment PQ in het middelpunt. Wees de punten

$P(1,4)$

$Q(5,-2).$

Zie de oplossing

Om de vergelijking van een lijn te bepalen, hebben we de richtingsvector nodig en een punt dat deel uitmaakt van de lijn.

In dit geval zal de richtingsvector van de lijn loodrecht op de vector staan

$\vv{PQ}.$

We berekenen daarom de vector

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

En we kunnen een vector loodrecht op een andere vinden door de componenten van de vector daartussen te veranderen en vervolgens het teken van een component te veranderen, dus:

$\vv{PQ}_\perp =(6,4)$

We hebben nu de richtingsvector van de lijn, dus we hebben nog maar één punt nodig dat bij de lijn hoort. In dit geval vertelt de instructie ons dat de lijn door het middelpunt van het segment gaat, dus berekenen we het middelpunt met behulp van de formule:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

Ten slotte construeren we de continue vergelijking van de lijn vanuit het berekende punt en de vector:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

Formule voor het midden van een segment

Wat is het middelpunt van een segment?

Hoe bereken je het middelpunt van een segment?

Oefeningen opgelost in het midden van een segment

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren