Op deze pagina leggen we uit wat lineair onafhankelijke en lineair afhankelijke vectoren zijn. U zult ook voorbeelden zien van hoe u kunt bepalen of een reeks vectoren lineair afhankelijk of onafhankelijk is. En daarnaast vind je stap voor stap oefeningen en opgeloste problemen over lineaire onafhankelijkheid en afhankelijkheid.
Wat zijn lineair onafhankelijke vectoren?
Een verzameling vrije vectoren is lineair onafhankelijk als geen van deze kan worden geschreven als een lineaire combinatie van de andere.
Met andere woorden, gegeven een reeks vectoren
![]()
Deze zijn lineair onafhankelijk als ze de enige oplossing zijn voor de volgende vergelijking:
![]()
Dit zijn alle coëfficiënten
![]()
gelijk aan 0:
![]()
Geometrisch zijn twee vectoren lineair onafhankelijk als ze niet dezelfde richting hebben, dat wil zeggen als ze niet evenwijdig zijn.
Kortheidshalve zeggen we soms rechtstreeks dat het LI-vectoren zijn. Of dat de vectoren lineaire onafhankelijkheid hebben.
Wat zijn lineair afhankelijke vectoren?
Het is duidelijk dat lineair afhankelijke vectoren het tegenovergestelde betekenen van lineair onafhankelijke vectoren. De definitie ervan is daarom:
Een verzameling vrije vectoren van het vlak is lineair afhankelijk als een van deze kan worden uitgedrukt als een lineaire combinatie van andere vectoren die het systeem vormen.
Met andere woorden, gegeven een reeks vectoren
![]()
Deze zijn lineair afhankelijk als er een oplossing bestaat voor de volgende vergelijking:
![]()
waarin een bepaalde coëfficiënt heeft
![]()
verschilt van 0:
![]()
Het omgekeerde is ook waar: als een vector een lineaire combinatie is van andere vectoren, dan zijn alle vectoren in de verzameling lineair afhankelijk.
Als twee vectoren parallel zijn, impliceert dit bovendien dat ze lineair afhankelijk zijn.
Soms worden ze ook afgekort en eenvoudigweg LD-vectoren genoemd. Of zelfs dat de vectoren een lineaire afhankelijkheid hebben.
Voorbeeld van hoe u kunt weten of vectoren lineair afhankelijk of onafhankelijk zijn
We zullen dan een typisch voorbeeld zien van lineair afhankelijke en onafhankelijke vectoren.
- Bepaal of de volgende 3 driedimensionale vectoren lineaire afhankelijkheid of onafhankelijkheid hebben:
![]()
![]()
![]()
Eerst moeten we de lineaire combinatievoorwaarde vermelden:
![]()
Nu vervangen we elke vector door zijn coördinaten. Zoals nul, wat overeenkomt met de nulvector:
![]()
Coëfficiënten vermenigvuldigen vectoren, dus de volgende uitdrukking is equivalent:
![]()
We voegen vectoren toe:
![]()
Als we goed kijken, komt de vorige uitdrukking overeen met 3 vergelijkingen, omdat elke coördinaat van de linkervector gelijk moet zijn aan elke coördinaat van de rechtervector. We hebben dus een homogeen systeem van 3 vergelijkingen met 3 onbekenden:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c6bb8117dd8ae715314efe73fe65eed8_l3.png)
Het enige dat we dus hoeven te doen, is het stelsel vergelijkingen oplossen waarvan de onbekenden zijn
![]()
En
![]()
Om dit te doen, kunt u elke methode gebruiken (substitutiemethode, Gaus-methode, Cramer-regel, enz.). Om echter te weten of de vectoren LI of LD zijn, is het voldoende om te bepalen of er een andere oplossing bestaat dan de triviale oplossing (alle coëfficiënten zijn gelijk aan nul). DUS:
- Als de determinant van de matrix bestaande uit de componenten van de vectoren verschillend is van nul, betekent dit dat het stelsel vergelijkingen slechts één oplossing heeft (
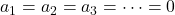
) en daarom zijn de vectoren lineair onafhankelijk
- Aan de andere kant, als de determinant van de matrix bestaande uit de componenten van de vectoren gelijk is aan nul, impliceert dit dat het stelsel vergelijkingen meer dan één oplossing heeft en dat de vectoren daarom lineair afhankelijk zijn.
Het enige dat dus berekend hoeft te worden is de determinant met de coördinaten van de vectoren (aangezien het een 3×3-determinant is, kan deze worden opgelost met de regel van Sarrus). Deze determinant komt overeen met de coëfficiënten van het vorige stelsel vergelijkingen:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-046e05ff603822985510c7bdc8b73021_l3.png)
In dit geval is de determinant verschillend van 0, dus de vectoren zijn lineair onafhankelijk .
Daarom is de enige mogelijke oplossing voor het stelsel vergelijkingen de triviale oplossing waarbij alle onbekenden gelijk zijn aan nul:
![]()
Eigenschappen van lineair afhankelijke en onafhankelijke vectoren
Lineaire afhankelijkheid of onafhankelijkheid van vectoren heeft de volgende kenmerken:
- Twee proportionele vectoren zijn evenwijdig en dus lineair afhankelijk omdat ze dezelfde richting hebben.
- Op dezelfde manier zijn twee vectoren, als ze niet dezelfde richting hebben of niet proportioneel zijn, lineair onafhankelijk.
- Drie coplanaire vectoren (die zich in hetzelfde vlak bevinden) zijn lineair onafhankelijk.
- De nulvector
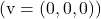
is lineair afhankelijk van elke vector.
- Een reeks lineair onafhankelijke vectoren genereert een vectorruimte en vormt een vectorbasis. Als de drie vectoren loodrecht staan, is het een orthogonale basis. En als de module ook gelijk is aan 1, komt dit overeen met een orthonormale basis.
Lineaire afhankelijkheids- en onafhankelijkheidsoefeningen opgelost
Hieronder heb je verschillende opgeloste oefeningen over lineair afhankelijke en onafhankelijke vectoren om te oefenen.
Oefening 1
Bepaal of de volgende vectoren lineair afhankelijk of onafhankelijk zijn:
![]()
![]()
![]()
We stellen eerst de lineaire combinatievoorwaarde:
![]()
![]()
![]()
![]()
De vorige gelijkheid komt overeen met het volgende systeem van lineaire vergelijkingen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-58f1b449f48096570437df0ca40f8a8d_l3.png)
Nadat we het stelsel vergelijkingen hebben vastgesteld, lossen we de determinant van de matrix op met zijn termen:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-caa6d4f135e79bb8b6d2368ff7eebefb_l3.png)
In dit geval is de determinant verschillend van 0, dus de drie vectoren zijn lineair onafhankelijk van elkaar.
Oefening 2
Classificeer de volgende vectoren als lineair afhankelijk of onafhankelijk:
![]()
![]()
![]()
Allereerst stellen we de vergelijking van de lineaire combinatie:
![]()
![]()
![]()
![]()
Uit de vorige gelijkheid verkrijgen we het volgende homogene systeem van vergelijkingen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c94610b6f8baef34a1fb4601c148f515_l3.png)
Nadat we het stelsel vergelijkingen hebben bepaald, lossen we de determinant van de matrix op met de coördinaten van de vectoren:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67678c37fdaf0955ef8bbab8d34379f8_l3.png)
In dit geval is de determinant gelijk aan 0, dus de drie vectoren zijn lineair van elkaar afhankelijk .
Oefening 3
Geef voor de volgende drie vectoren aan welke vectorparen lineair afhankelijk zijn en welke paren lineair onafhankelijk zijn.
![]()
De eenvoudigste manier om te bepalen of een paar vectoren lineair afhankelijk of onafhankelijk is, is door te controleren of ze proportioneel zijn.
We controleren eerst de vector
![]()
met de vector
![]()
![]()
Ten tweede controleren we de vector
![]()
met de vector
![]()
![]()
Ten slotte testen we de vector
![]()
met de vector
![]()
![]()
Het enige paar vectoren dat lineair van elkaar afhangt, is dus
![]()
En
![]()
Bovendien is hun relatie als volgt:
![]()
Of gelijkwaardig:
![]()
Aan de andere kant zijn de andere paren vectoren lineair onafhankelijk.
Oefening 4
Bestudeer de lineaire afhankelijkheid of onafhankelijkheid van de volgende 4 vectoren van elkaar:
![]()
![]()
![]()
![]()
We stellen eerst de lineaire combinatievoorwaarde:
![]()
![]()
![]()
![]()
In dit geval hebben we een stelsel van 3 vergelijkingen met 4 onbekenden:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9451263e5a31994569292e32666d93e_l3.png)
We kunnen de determinant van de gehele systeemmatrix niet oplossen, aangezien alleen vierkante matrices kunnen worden bepaald. We moeten daarom alle mogelijke combinaties van 3×3 determinanten berekenen en kijken of één ervan gelijk is aan 0, in welk geval de vectoren lineair afhankelijk zullen zijn. Aan de andere kant, als alle determinanten verschillend zijn van 0, zullen de 4 vectoren dat ook zijn. lineair onafhankelijk zijn.
We berekenen de determinant van de coëfficiënten
![]()
En
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-488d7848a40aa9a91bd5b3aa1f09b774_l3.png)
De determinant van de eerste 3 coëfficiënten (of de eerste 3 vectoren) is verschillend van nul. Dus nu proberen we met de determinant van de coëfficiënten
![]()
En
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1475a77f10ea0c16147a6f9c3f611b4_l3.png)
We hebben een nuldeterminant verkregen, dus het is niet nodig om de andere determinanten te berekenen, omdat we al weten dat de 4 vectoren lineair afhankelijk zijn.
Oefening 5
Bereken de waarde van
![]()
zodat de volgende vectoren lineair onafhankelijk zijn:
![]()
![]()
![]()
Allereerst stellen we de vergelijking van de lineaire combinatie:
![]()
![]()
![]()
![]()
Uit de vorige vectorvergelijking verkrijgen we het volgende homogene stelsel van vergelijkingen:
![Rendered by QuickLaTeX.com \left. \begin{array}{l}3a_1-2a_2+a_3= 0 \\[2ex] -a_1+4a_2+3a_3 =0\\[2ex] 5a_1+7a_2+ka_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16f88cbf406c1faf61307b99179a5de6_l3.png)
Nadat we het stelsel vergelijkingen hebben vastgesteld, gaan we proberen de determinant van het stelsel op te lossen:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3&-2&1\\[1.1ex] -1&4&3 \\[1.1ex] 5&7&k \end{vmatrix} =10k-120](https://mathority.org/wp-content/ql-cache/quicklatex.com-d748080bb1cacc1c80a35ef633a2d85e_l3.png)
De verklaring vertelt ons dat de vectoren lineair afhankelijk moeten zijn. De determinant moet daarom gelijk zijn aan nul:
![]()
![]()
![]()
![]()
De constante moet daarom gelijk zijn aan 12, zodat de vectoren een lineaire afhankelijkheid hebben.