Een matrix diagonaliseren -

Op deze pagina vindt u alles over diagonaliseerbare matrices: wat ze zijn, wanneer ze kunnen worden gediagonaliseerd en wanneer niet, de methode om matrices te diagonaliseren, de toepassingen en eigenschappen van deze specifieke matrices, etc. En je hebt zelfs verschillende oefeningen stap voor stap opgelost, zodat je kunt oefenen en perfect kunt begrijpen hoe ze gediagonaliseerd zijn. Ten slotte leren we ook hoe we matrixdiagonalisaties kunnen uitvoeren met het computerprogramma MATLAB, aangezien dit zeer vaak gebruikt wordt.

Wat is een diagonaliseerbare matrix?

Zoals we hieronder zullen zien, is het diagonaliseren van een matrix erg handig op het gebied van lineaire algebra. Dit is de reden waarom velen zich afvragen… wat is matrixdiagonalisatie? Welnu, de definitie van een diagonaliseerbare matrix is:

Een diagonaliseerbare matrix is een vierkante matrix die kan worden omgezet in een diagonale matrix, dat wil zeggen een matrix gevuld met nullen behalve op de hoofddiagonaal. De diagonalisatie van matrices wordt als volgt opgesplitst:

$A = PDP^{-1}$

Of gelijkwaardig,

$D = P^{-1}AP$

Goud

$A$

is de matrix om te diagonaliseren,

$P$

is de matrix waarvan de kolommen de eigenvectoren (of eigenvectoren) zijn

$A$

$P^{-1}$

de inverse matrix en

$D$

is de diagonale matrix gevormd door de eigenwaarden (of eigenwaarden) van

$A$

De matrix

$P$

fungeert als een basisveranderingsmatrix, dus eigenlijk veranderen we met deze formule de basis in matrix

$A$

, zodat de matrix een diagonale matrix wordt (

$D$

) in de nieuwe basis.

Daarom de matrix

$A$

en de matrix

$D$

Het zijn vergelijkbare matrices. En uiteraard,

$P$

Het is een reguliere of niet-gedegenereerde matrix.

Wanneer kun je een matrix diagonaliseren?

Niet alle matrices kunnen diagonaliseerd worden; alleen matrices die aan bepaalde kenmerken voldoen, kunnen worden gediagonaliseerd. Je kunt op verschillende manieren zien of een matrix diagonaliseerbaar is:

Een vierkante matrix van orde n is diagonaliseerbaar als deze n lineair onafhankelijke eigenvectoren (of eigenvectoren) heeft, of met andere woorden, als deze vectoren een basis vormen. Dit komt omdat de matrix
$P$

, die wordt gebruikt om een matrix te diagonaliseren, wordt gevormd door de eigenvectoren van genoemde matrix. Om te weten of de eigenvectoren LI zijn, volstaat het dat de determinant van de matrix

$P$

verschilt van 0, wat betekent dat de matrix de maximale rangorde heeft.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Een eigenschap van eigenwaarden en eigenvectoren is dat eigenvectoren van verschillende eigenwaarden lineair onafhankelijk zijn. Als alle eigenwaarden van de matrix uniek zijn, is de matrix daarom diagonaliseerbaar.

Een andere manier om te bepalen of een matrix in een diagonale matrix kan worden ondergebracht, is door gebruik te maken van algebraïsche en geometrische veelvouden. Algebraïsche multipliciteit is het aantal keren dat een eigenwaarde (of eigenwaarde) wordt herhaald, en geometrische multipliciteit is de dimensie van de kern (of kern) van de matrix door de eigenwaarde op de hoofddiagonaal af te trekken. Dus als voor elke eigenwaarde de algebraïsche multipliciteit gelijk is aan de geometrische multipliciteit , is de matrix diagonaliseerbaar.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Ten slotte is er een stelling, de spectrale stelling, die de diagonalisatie van symmetrische matrices met reële getallen garandeert. Met andere woorden: elke reële en symmetrische matrix is diagonaliseerbaar .

Hoe een matrix te diagonaliseren

De procedure voor het diagonaliseren van een matrix is gebaseerd op het vinden van de eigenwaarden (of eigenwaarden) en eigenvectoren (of eigenvectoren) van een matrix. Daarom is het belangrijk dat je beheerst hoe je de eigenwaarden (of eigenwaarden) en eigenvectoren (of eigenvectoren) van elke matrix kunt berekenen . U kunt zich herinneren hoe het werd gedaan door op de link te klikken, waar we stap voor stap uitleggen hoe u ze kunt vinden en enkele trucs die de berekeningen veel gemakkelijker maken. Daarnaast vind je ook opgeloste oefeningen om te oefenen.

Met de volgende methode kunt u een matrix van elke afmeting diagonaliseren: 2×2, 3×3, 4×4, enz. De te volgen stappen om een matrix te diagonaliseren zijn:

Verkrijg de eigenwaarden (of eigenwaarden) van de matrix.
Bereken de eigenvector die bij elke eigenwaarde hoort.
Construeer de matrix
$P$

, waarvan de kolommen de eigenvectoren zijn van de te diagonaliseren matrix.
Controleer of de matrix diagonaliseerbaar is (deze moet voldoen aan een van de voorwaarden die in de vorige sectie zijn uitgelegd).
Construeer de diagonale matrix
$D$

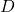
, waarvan de elementen allemaal 0 zijn, behalve die op de hoofddiagonaal, dit zijn de eigenwaarden gevonden in stap 1.

Waarschuwing: de eigenvectoren van de matrix

$P$

kunnen in elke volgorde worden geplaatst, behalve de eigenwaarden van de diagonaalmatrix

$D$

Ze moeten in dezelfde volgorde worden geplaatst. Bijvoorbeeld de eerste eigenwaarde van de diagonaalmatrix

$D$

moet degene zijn die overeenkomt met de eigenvector van de eerste kolom van de matrix

$P$

Hieronder staan een aantal stapsgewijze matrixdiagonalisatie-oefeningen waarmee je kunt oefenen.

Matrix-diagonalisatie-oefeningen opgelost

Oefening 1

Diagonaliseer de volgende vierkante matrix met afmeting 2×2:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Zie de oplossing

We moeten eerst de eigenwaarden van de matrix A bepalen. We berekenen daarom de karakteristieke vergelijking door de volgende determinant op te lossen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Laten we nu de wortels van de karakteristieke polynoom berekenen:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Zodra de eigenwaarden zijn verkregen, berekenen we de eigenvector die bij elke eigenwaarde hoort. Ten eerste de eigenvector die overeenkomt met de eigenwaarde 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

En dan berekenen we de eigenvector die hoort bij de eigenwaarde 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Wij bouwen de matrix

$P$

, gevormd door de eigenvectoren van de matrix:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Omdat alle eigenwaarden verschillend zijn, is de matrix A diagonaliseerbaar. De overeenkomstige diagonale matrix is dus degene die de eigenwaarden op de hoofddiagonaal heeft:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Bedenk dat de eigenwaarden in dezelfde volgorde moeten worden geplaatst als de eigenvectoren in de matrix

$P$

Concluderend zijn de basisveranderingsmatrix en de diagonale matrix:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Oefening 2

Diagonaliseer de volgende vierkante matrix van orde 2:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Zie de oplossing

We moeten eerst de eigenwaarden van de matrix A bepalen. We berekenen daarom de karakteristieke vergelijking door de volgende determinant op te lossen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Laten we nu de wortels van de karakteristieke polynoom berekenen:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Zodra de eigenwaarden zijn verkregen, berekenen we de eigenvector die bij elke eigenwaarde hoort. Ten eerste de eigenvector die overeenkomt met de eigenwaarde -1:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

En dan berekenen we de eigenvector die hoort bij de eigenwaarde 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Wij bouwen de matrix

$P$

, gevormd door de eigenvectoren van de matrix:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Omdat alle eigenwaarden van elkaar verschillen, is matrix A diagonaliseerbaar. De overeenkomstige diagonale matrix is dus degene die de eigenwaarden op de hoofddiagonaal bevat:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Bedenk dat de eigenwaarden in dezelfde volgorde moeten worden geplaatst als de eigenvectoren in de matrix

$P$

Concluderend zijn de basisveranderingsmatrix en de diagonale matrix:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Oefening 3

Diagonaliseer de volgende vierkante matrix met afmeting 3×3:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Zie de oplossing

De eerste stap bestaat uit het vinden van de eigenwaarden van de matrix A. We berekenen daarom de karakteristieke vergelijking door de determinant van de volgende matrix op te lossen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

We moeten nu de wortels van de karakteristieke polynoom berekenen. Omdat het een polynoom van de derde graad is, passen we de regel van Ruffini toe:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

En dan vinden we de wortels van de verkregen polynoom:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

De eigenwaarden van de matrix zijn dus:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

Zodra de eigenwaarden zijn gevonden, berekenen we de eigenvector die bij elk ervan hoort. Ten eerste de eigenvector die overeenkomt met de eigenwaarde 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Vervolgens berekenen we de eigenvector die hoort bij de eigenwaarde 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

En tenslotte berekenen we de eigenvector die hoort bij de eigenwaarde 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Wij bouwen de matrix

$P$

, gevormd door de eigenvectoren van de matrix:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Omdat alle eigenwaarden van elkaar verschillen, is matrix A diagonaliseerbaar. De overeenkomstige diagonale matrix is dus degene die de eigenwaarden op de hoofddiagonaal heeft:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Bedenk dat de eigenwaarden in dezelfde volgorde moeten worden geplaatst als de eigenvectoren in de matrix

$P$

Kort gezegd zijn de basisveranderingsmatrix en de diagonaliseerde matrix:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Oefening 4

Diagonaliseer, indien mogelijk, de volgende vierkante matrix van orde 3:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Zie de oplossing

De eerste stap bestaat uit het vinden van de eigenwaarden van de matrix A. We berekenen daarom de karakteristieke vergelijking door de determinant van de volgende matrix op te lossen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

We moeten nu de wortels van het minimumpolynoom berekenen. Omdat het een polynoom van de derde graad is, passen we de regel van Ruffini toe om het in factoren te ontbinden:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

En dan vinden we de wortels van de verkregen polynoom:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

De eigenwaarden van de matrix zijn dus:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

De eigenwaarde van -2 heeft een eenvoudige algebraïsche multipliciteit, terwijl de eigenwaarde van 2 een dubbele multipliciteit heeft.

Zodra de eigenwaarden zijn gevonden, berekenen we de eigenvector die bij elk ervan hoort. Ten eerste de eigenvector die overeenkomt met de eigenwaarde -2:

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Laten we nu de eigenvectoren berekenen die bij de eigenwaarden 2 horen.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Omdat de eigenwaarde 2 twee keer wordt herhaald, moeten we een andere eigenvector berekenen die voldoet aan de deelruimte- (of eigenruimte-)vergelijkingen:

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Wij bouwen de matrix

$P$

, gevormd door de drie eigenvectoren van de matrix:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

De drie vectoren zijn echter niet lineair onafhankelijk, aangezien de twee eigenvectoren met eigenwaarde 2 uiteraard een lineaire combinatie van elkaar zijn. Dit kan ook worden aangetoond omdat de determinant van de matrix

$P$

is gelijk aan 0 (heeft een regel vol nullen):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Omdat de eigenvectoren lineair afhankelijk zijn, is de matrix A daarom niet diagonaliseerbaar .

Oefening 5

diagonaliseer indien mogelijk de volgende vierkante matrix van maat 3×3:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Zie de oplossing

De eerste stap bestaat uit het vinden van de eigenwaarden van de matrix A. We berekenen daarom de karakteristieke vergelijking door de determinant van de volgende matrix op te lossen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

Omdat de eerste regel volledig uit nullen bestaat, behalve 3, zullen we hiervan profiteren om de determinant van de matrix op te lossen met behulp van cofactoren (of adjuncten):

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

We moeten nu de wortels van de karakteristieke polynoom berekenen. Het is beter om de haakjes niet te vermenigvuldigen, omdat je dan een derdegraadspolynoom krijgt. Aan de andere kant, als de twee factoren afzonderlijk worden opgelost, is het gemakkelijker om de eigenwaarden te verkrijgen:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

De eigenwaarden van de matrix zijn dus:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

Zodra de eigenwaarden zijn gevonden, berekenen we de eigenvector die bij elk ervan hoort. Ten eerste de eigenvector die overeenkomt met de eigenwaarde 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Vervolgens berekenen we de eigenvectoren die bij de eigenwaarden 3 horen:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Omdat de eigenwaarde 3 tweemaal wordt herhaald, moeten we een andere eigenvector berekenen die aan de eigenruimtevergelijkingen voldoet:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Wij bouwen de matrix

$P$

, gevormd door de eigenvectoren van de matrix:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

In tegenstelling tot oefening 4 konden we in dit geval 3 lineair onafhankelijke vectoren vormen, hoewel de algebraïsche multipliciteit van de eigenwaarde 3 dubbel is. Dit kan worden geverifieerd door te zien dat de determinant van de matrix

$P$

geeft een resultaat dat verschilt van 0:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

We kunnen dus de diagonale ontbinding van matrix A uitvoeren. En de overeenkomstige diagonale matrix is degene die de eigenwaarden op de hoofddiagonaal heeft:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Bedenk dat de eigenwaarden in dezelfde volgorde moeten worden geplaatst als de eigenvectoren in de matrix

$P$

Kort gezegd is de basisveranderingsmatrix die nodig is om de matrix en zijn diagonale vorm te diagonaliseren:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Oefening 6

Voer indien mogelijk de diagonalisatie uit van de volgende matrix met afmeting 4×4:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Zie de oplossing

De eerste stap bestaat uit het vinden van de eigenwaarden van de matrix A. We berekenen daarom de karakteristieke vergelijking door de determinant van de volgende matrix op te lossen:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

In dit geval bestaat de laatste kolom van de determinant alleen uit nullen, behalve één element. We zullen hiervan profiteren om de determinant via cofactoren via deze kolom te berekenen:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

We moeten nu de wortels van de karakteristieke polynoom berekenen. Het is beter om het product van de haakjes niet te doen, omdat je dan een polynoom van de vierde graad krijgt. Als de twee factoren echter afzonderlijk worden opgelost, is het eenvoudiger om de eigenwaarden te berekenen:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

De eigenwaarden van de matrix zijn dus:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

Zodra alle eigenwaarden zijn gevonden, gaan we richting de eigenvectoren. We berekenen de eigenvector die hoort bij de eigenwaarde 0:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

We berekenen de eigenvector die hoort bij de eigenwaarde -3:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

We berekenen de eigenvector die hoort bij de eigenwaarde 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

We berekenen de eigenvector die hoort bij de eigenwaarde 5:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Wij maken de matrix

$P$

, samengesteld uit de eigenvectoren van de matrix:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

Omdat alle eigenwaarden van elkaar verschillen, is matrix A diagonaliseerbaar. De overeenkomstige diagonale matrix is dus degene die de eigenwaarden op de hoofddiagonaal heeft:

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Houd er rekening mee dat de eigenwaarden in dezelfde volgorde moeten worden geplaatst als de eigenvectoren in de matrix

$P$

Samenvattend zijn de fundamentele matrixveranderingen die nodig zijn om matrix A en de matrix in diagonale vorm te diagonaliseren:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Toepassingen van diagonaliseerbare matrices

Als je zo ver bent gekomen, vraag je je waarschijnlijk af: waar is een diagonaliseerbare matrix voor?

Welnu, diagonaliseerbare matrices zijn erg nuttig en worden veel gebruikt in de wiskunde. De reden is dat een diagonaalmatrix vrijwel vol nullen staat en berekeningen daardoor veel eenvoudiger maakt.

Een duidelijk voorbeeld hiervan zijn de machten van diagonaliseerbare matrices, omdat hun resultaat wordt vereenvoudigd door de volgende formule:

$\displaystyle A^k=PD^kP^{-1}$

Deze gelijkheid kan eenvoudig worden bewezen door inductie. Het is daarom voldoende om de matrix te verhogen

$D$

aan de exposant. En aangezien het een diagonale matrix is, wordt de bewerking beperkt tot het verhogen van elke term van de hoofddiagonaal tot de exponent:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Voorbeeld van de macht van een diagonaliseerbare matrix

Om het beter te begrijpen, zullen we als voorbeeld de kracht van een diagonaliseerbare matrix berekenen:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

De fundamentele veranderingsmatrix

$P$

, gevormd door zijn eigenvectoren, en de diagonale matrix

$D$

, samengesteld uit zijn eigen waarden, zijn:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Om een voorbeeld te geven: de matrix A verhoogd tot 7 is gelijk aan:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Nu keren we de matrix om

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

We lossen de kracht van de matrix op

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

En ten slotte voeren we de vermenigvuldigingen van de matrices uit:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Zoals je hebt gezien, is het handiger om de macht te berekenen met een diagonale matrix dan dezelfde matrix zeven keer achter elkaar te vermenigvuldigen. Stel je dan voor met veel grotere exponentwaarden.

Eigenschappen van diagonaliseerbare matrices

De kenmerken van dit type matrix zijn:

Als de matrix
$A$

is diagonaliseerbaar, elke macht van

$A$

.

Bijna alle matrices kunnen in een complexe omgeving worden gediagonaliseerd
$\mathbb{C}$

. Hoewel je hieronder de uitzonderingen hebt die nooit diagonaliseerbaar zijn.

Als de matrix
$P$

een orthogonale matrix is, dan zeggen we dat de matrix

$A$

is orthogonaal diagonaliseerbaar en daarom kan de vergelijking herschreven worden:

$\displaystyle A=PDP^t$

Een matrix is diagonaliseerbaar door een unitaire matrix als en slechts als het een normale matrix is.

Gegeven twee diagonaliseerbare matrices zijn ze commuteerbaar als en slechts als ze gelijktijdig kunnen worden gediagonaliseerd, dat wil zeggen als ze dezelfde orthonormale basis van eigenvectoren (of eigenvectoren) delen.

Als een endomorfisme diagonaliseerbaar is, zeggen we dat het diagonaliseerbaar is door gelijkenis . Niet alle endomorfismen zijn echter diagonaliseerbaar, of met andere woorden: de diagonalisatie van een endomorfisme is niet verzekerd.

Gelijktijdige diagonalisatie

Er wordt gezegd dat een reeks matrices gelijktijdig diagonaliseerbaar is als er een inverteerbare matrix bestaat die als basis dient voor het diagonaliseren van elke matrix in deze reeks. Met andere woorden, als twee matrices op dezelfde eigenvectorbasis diagonaliseren, betekent dit dat ze gelijktijdig diagonaliseerbaar zijn.

Bovendien, zoals we hebben opgemerkt bij de eigenschappen van matrixdiagonalisatie, moeten twee matrices, als ze gelijktijdig kunnen diagonaliseren, met elkaar pendelen.

De volgende twee matrices zijn bijvoorbeeld commuteerbaar, dus diagonaliseren ze op dezelfde basis van eigenvectoren of eigenvectoren.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Zelfs als ze dezelfde eigenvectoren hebben, betekent dat niet dat ze dezelfde eigenwaarden hebben. Hoewel de matrices A en B hierboven vergelijkbare eigenvectoren hebben, hebben ze in feite verschillende eigenwaarden.

Niet-diagonaliseerbare matrices

Hoewel de overgrote meerderheid van de matrices diagonaliseerbaar is in een omgeving met complexe getallen, kunnen sommige matrices nooit diagonaliseerd worden.

Dit feit doet zich voor wanneer de algebraïsche veelheid van een eigenwaarde (of eigenwaarde) niet samenvalt met de geometrische veelheid.

De volgende matrix kan bijvoorbeeld op geen enkele manier worden gediagonaliseerd, maar is ‘indiagonaliseerbaar’:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

Bovendien zijn er matrices die niet in staat zijn tot diagonalisatie in een omgeving met reële getallen, maar die wel diagonaliseren bij het werken met complexe getallen, zoals deze matrix:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Ten slotte zijn er enkele diagonalisatieprocedures voor matrixblokken die niet puur diagonaliseerbaar zijn, maar iets ingewikkelder zijn. De bekendste methode is diagonalisatie met de canonieke vorm van Jordanië .

Diagonaliseer een matrix met MATLAB

Computerprogramma’s zijn erg handig als het gaat om het diagonaliseren van matrices, vooral als ze erg groot zijn. En de bekendste software is zeker MATLAB , dus nu zullen we zien hoe we een matrix diagonaal kunnen ontbinden met behulp van dit programma.

De instructie die wordt gebruikt om een matrix te diagonaliseren met MATLAB is:

$\displaystyle \text{[P, D] = eig(A)}$

Goud

$A$

is de matrix die moet worden gediagonaliseerd en

$P$

$D$

zijn de matrices die het programma retourneert:

$P$

is de matrix gevormd door de eigenvectoren en

$D$

is de matrix in diagonale vorm waarvan de belangrijkste diagonale termen de eigenwaarden zijn.

Daarom hoeft u alleen deze code in het programma in te voeren.

Aan de andere kant, als u alleen de eigenwaarden wilt weten, kunt u de volgende verklaring gebruiken:

$\displaystyle e= eig(A)}$

Goud

$e$

is de kolomvector die MATLAB retourneert met de eigenwaarden van de matrix

$A$

Wat is een diagonaliseerbare matrix?

Wanneer kun je een matrix diagonaliseren?

Hoe een matrix te diagonaliseren

Matrix-diagonalisatie-oefeningen opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Toepassingen van diagonaliseerbare matrices

Voorbeeld van de macht van een diagonaliseerbare matrix

Eigenschappen van diagonaliseerbare matrices

Gelijktijdige diagonalisatie

Niet-diagonaliseerbare matrices

Diagonaliseer een matrix met MATLAB

Laat een reactie achter Reactie annuleren