Op deze pagina leggen we uit wat een perfecte vierkante trinominale is en hoe deze wordt verantwoord. Bovendien kun je verschillende voorbeelden zien en oefenen met stapsgewijze perfecte vierkante trinomiale oefeningen.
Wat is een perfecte vierkante trinominaal?
Het is duidelijk dat je, voordat je de betekenis van een perfecte vierkante trinominaal ziet, moet weten wat trinomialen zijn, dus ik raad aan om deze gelinkte pagina te bekijken (waar het in detail wordt uitgelegd) voordat je verdergaat.
De definitie van een perfecte vierkante trinominaal is dus als volgt:
In de wiskunde is een perfecte vierkante trinominaal , ook bekend als TCP , de trinominaal die wordt verkregen door een binomiaal te kwadrateren.
Daarom bestaat een perfect vierkante trinominaal uit een polynoom met twee perfecte vierkanten en een andere term die het dubbele product is van de basissen van deze vierkanten.

Zoals je kunt zien aan de hand van de twee bovenstaande formules, wordt de perfecte vierkante trinominale verkregen uit twee opmerkelijke identiteiten (of opmerkelijke producten), en daarom is het zo belangrijk. Concreet wordt een perfecte vierkante trinominale gevonden bij het oplossen van het kwadraat van een optelling of het kwadraat van een aftrekking .
Perfecte vierkante trinomiale voorbeelden
Om het concept van de perfecte vierkante trinominaal te begrijpen, zullen we stap voor stap twee voorbeelden uitleggen:
voorbeeld 1
![]()
Dit voorbeeld is een perfecte vierkante trinominale omdat er in de algebraïsche uitdrukking twee perfecte vierkanten zijn (dat wil zeggen, ze hebben een exacte vierkantswortel), aangezien
![]()
en 9 zijn gelijkwaardig aan
![]()
en 3 respectievelijk verhoogd tot de macht twee:
![]()
![]()
En meer nog, de laatst overgebleven term van de trinominaal
![]()
Het wordt verkregen door de bases van de twee voorgaande vierkanten samen te vermenigvuldigen en met 2:
![]()
Dus de hele opmerkelijke identiteit in deze oefening zou zijn:
![]()
Voorbeeld 2
![]()
Dit andere voorbeeld is ook een perfect vierkante trinominale omdat aan de 3 noodzakelijke voorwaarden is voldaan: twee termen komen overeen met twee perfecte vierkanten, en een andere term is het resultaat van het vermenigvuldigen van de bases van deze vierkanten met elkaar en met 2.
![]()
![]()
![]()
In dit geval heeft de perfecte vierkante trinominale een negatieve monomial, en komt daarom overeen met de ontwikkeling van de opmerkelijke gelijkheid van een kwadraatverschil:
![]()
Hoe u een perfecte vierkante trinominaal kunt ontbinden
In de algebra is een veel voorkomend probleem het ontbinden van een perfecte vierkante trinominaal (PCT). Voor het geval je niet weet wat dat betekent: het ontbinden van een polynoom in factoren betekent dat de uitdrukking ervan wordt omgezet in een product van factoren.
Om dit type algebraïsche trinomiaal in factoren te factoriseren, moeten de volgende regels worden gerespecteerd:
- De trinominale moet twee perfecte vierkanten hebben, die we zullen noemen
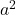
En
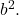
- De derde resterende term van de trinominaal moet gelijk zijn aan het dubbele product van de bases van de twee perfecte vierkanten, wat wiskundig overeenkomt met de uitdrukking
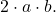
- De gefactoriseerde trinominaal zal zijn
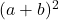
als alle termen van de perfecte vierkante trinominaal positief zijn, anders, als het dubbele product van de basissen van de vierkanten een negatief teken heeft, zal de in factoren verwerkte trinominaal zijn
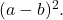
Om de procedure te begrijpen, zullen we stap voor stap een oefening oplossen:
- Factor de volgende perfecte vierkante trinominaal:
![]()
Het eerste dat we moeten doen is vaststellen of de trinominaal twee elementen heeft die perfecte vierkanten zijn, of met andere woorden, of de vierkantswortel geen decimaal getal oplevert. Bij dit probleem
![]()
is het kwadraat van de variabele
![]()
en 36 is het kwadraat van 6:
![]()
![]()
De trinominaal heeft dus twee perfecte vierkanten.
Ten tweede moeten we controleren of de tussenterm equivalent is aan het dubbelproduct van de twee wortels berekend in de vorige stap:
![]()
Deze regel wordt ook gerespecteerd.
Dan is aan alle voorwaarden voldaan. Daarom is de in rekening gebrachte perfecte vierkante trinominaal de binomiaal gevormd door de twee gevonden wortels (
![]()
en het getal 6) in het kwadraat:
![]()
Omdat de tussenterm negatief is, moeten we ook een minteken tussen haakjes zetten. Aan de andere kant, als het positief was, zouden we een bedrag moeten toevoegen:
![]()
Logischerwijs is ontbinden in factoren een ingewikkelde procedure. Daarom raad ik u aan om naast de onderstaande oefening ook eens naar deze voorbeelden van veeltermen in factoren te kijken. In deze link leggen we ook een methode uit die niet alleen wordt gebruikt om trinomialen te ontbinden, maar ook elk type polynoom, en net zo snel.
Opgeloste oefeningen van de perfecte vierkante trinominale
Transformeer de volgende trinomialen in vierkante binomialen door de overeenkomstige formule toe te passen:
![]()
![]()
![]()
![]()
![]()
Om een perfecte vierkante trinominaal om te zetten in de macht van een vierkante binomiaal, moet je de formules gebruiken voor de opmerkelijke identiteiten van het kwadraat van een som en het kwadraat van een verschil, namelijk:
![]()
![]()
Nog:
![]()
![]()
![]()
![]()
![]()
⬇⬇⬇ Vergeet niet dat je ons al je vragen hieronder in de reacties kunt schrijven! ⬇⬇⬇