Polynomiale ontleding (of uitdrukking) van een getal

Op deze pagina leggen we uit hoe je de polynomiale ontbinding (of uitdrukking) van een getal uitvoert. Hier zie je voorbeelden van polynomiale ontbindingen en daarnaast vind je opgeloste stap-voor-stap oefeningen om te oefenen.

Wat is polynomiale ontbinding van een getal?

In de wiskunde bestaat de polynomiale ontbinding van een getal uit het uitdrukken van dat getal in een som, zodat elke term van de som een product is van elk cijfer van het getal met een macht van grondtal 10.

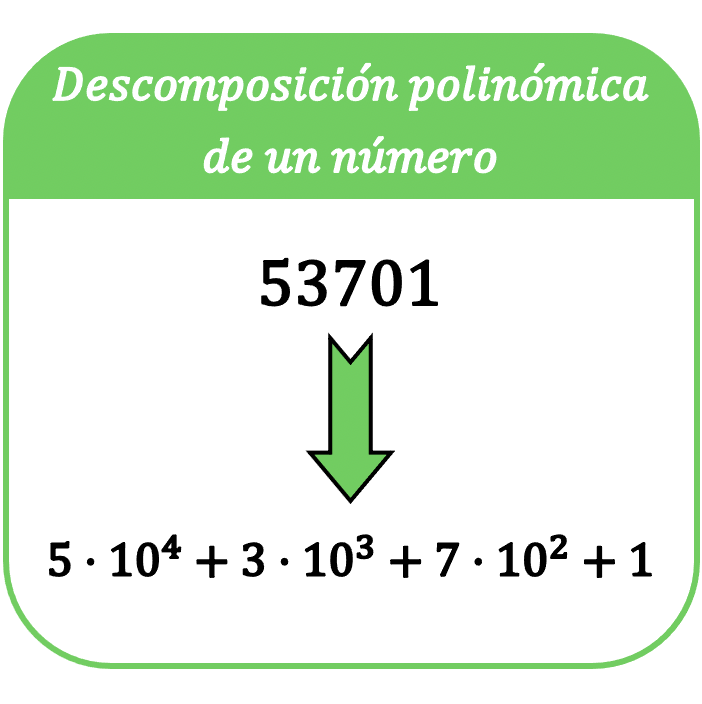
De term polynomiale ontleding van een getal wordt ook wel polynoomuitdrukking van een getal genoemd.

Hoe een polynomiale ontbinding uit te voeren

Om een polynoomontbinding van een getal uit te voeren, moet u elk cijfer van het getal met 10 vermenigvuldigen, verhoogd tot het aantal cijfers aan de rechterkant .

Als we bijvoorbeeld de polynoomontbinding van het volgende getal willen berekenen:

In dit geval staat het getal 8 op de vijfde positie en heeft het dus 4 cijfers aan de rechterkant. We moeten daarom acht met tien vermenigvuldigen tot de macht van vier:

Om het getal 86293 polynoom te ontbinden, moet je dus hetzelfde doen met alle cijfers van het getal, en alle vermenigvuldigingen uitdrukken in de vorm van een som:

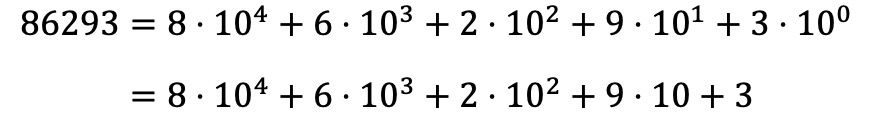
Merk op dat de macht 10 ⁰ verdwijnt omdat, volgens de eigenschappen van machten, elk getal verhoogd tot 0 gelijk is aan 1, dus 10 ⁰ = 1.

Aan de andere kant kun je de polynomiale ontbinding van een getal ook vinden aan de hand van de multiplicatieve ontleding:

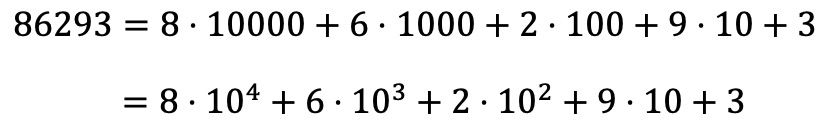
Voorbeelden van polynoomontbindingen van getallen

Als we eenmaal hebben gezien hoe de polynomiale ontbinding van een getal wordt uitgevoerd, zullen we verschillende voorbeelden van dit soort bewerkingen zien om het concept volledig te begrijpen.

• Polynomiale ontleding van 3641:

• Polynomiale ontleding van 56912:

• Polynomiale ontleding van 27084:

In dit laatste voorbeeld kunnen we de derde vermenigvuldiging vereenvoudigen, aangezien elk getal vermenigvuldigd met nul teniet wordt gedaan.

Polynomiale ontleding van decimale getallen

We hebben zojuist gezien hoe we de polynomiale ontbinding van de natuurlijke getallen moeten uitvoeren. Maar… hoe ontleed je een decimaal getal polynomiaal?

Welnu, de polynomiale ontbinding met decimale getallen gebeurt op dezelfde manier als met gehele getallen, maar daarnaast voegen we het product toe van elk decimaal cijfer vermenigvuldigd met een macht van grondtal 10, waarvan de exponent de decimale positie is die wordt ingenomen door het genoemde cijfer met een negatief getal. teken.

In woorden uitgelegd kan dit erg ingewikkeld lijken, maar je zult zien dat het met een voorbeeld beter begrepen wordt:

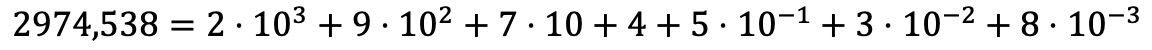
Opgeloste polynomiale ontledingsoefeningen

Om je te laten oefenen met het ontleden van polynomen, hebben we verschillende oefeningen voorbereid die je stap voor stap kunt oplossen.

Vergeet niet dat je ons al je vragen kunt stellen in de reacties! 🤔🤔🤔

Oefening 1

Voer de polynomiale ontbinding van de volgende getallen uit:

Om de polynomiale ontbinding van een willekeurig getal te vinden, vermenigvuldigt u elk cijfer van dat getal met 10 met het aantal cijfers aan de rechterkant, en telt u vervolgens alle vermenigvuldigingen bij elkaar op. Nog:

Oefening 2

Zoek de polynomiale ontbinding van de volgende getallen:

Om een getal polynomiaal te ontleden, moet je elk cijfer van dat getal met tien vermenigvuldigen met het aantal cijfers rechts ervan, en vervolgens alle producten bij elkaar optellen. Nog:

Oefening 3

Bereken de polynomiale ontbinding van de volgende decimale getallen:

In dit probleem zijn alle getallen decimaal, dus om ze te ontleden moet je elk niet-decimaal cijfer vermenigvuldigen met 10, verhoogd tot het aantal cijfers dat het heeft tot aan de komma, en elk decimaal cijfer vermenigvuldigen met 10, verhoogd tot de decimale positie met een negatief teken.