Newton's binominale (binominale stelling)

Op deze pagina vindt u de uitleg van wat de binomiale (of binominale stelling) van Newton is en wat de formule ervan is. Je kunt ook zien hoe dit vereenvoudigd kan worden met de Tartaglia (of Pascal) driehoek. Daarnaast vind je stap-voor-stap opgeloste oefeningen voor de binomiaal van Newton en al zijn eigenschappen. Ten slotte zullen we de curiosa achter de oorsprong van deze zeer specifieke stelling uitleggen.

Wat is de binomiaal van Newton?

In de wiskunde is de binomiale stelling van Newton , ook bekend als de binomiale stelling , een formule waarmee je eenvoudig de macht van een binominale waarde kunt berekenen. Met andere woorden, de binomiale waarde van Newton bestaat uit een formule waarmee algebraïsche uitdrukkingen van de vorm (a+b) kunnen worden opgelost .

Het is duidelijk dat deze stelling is vernoemd naar de natuurkundige, wiskundige en filosoof Sir Isaac Newton. Er bestaat echter enige controverse in dit opzicht, aangezien er teksten uit het Midden-Oosten zijn gevonden waarin deze stelling al in gebruik was. Hieronder zullen we de oorsprong van deze wiskundige formule diepgaand bespreken.

De binomiale formule van Newton

Zoals we hebben gezien bij de definitie van de binominale term van Newton, wordt deze stelling gebruikt om de machten van binominale getallen op te lossen. Maar… hoe wordt de binominale toepassing van Newton toegepast? Of, met andere woorden, wat is de binomiale formule van Newton?

De wiskundige formule voor de binomiaal van Newton is als volgt:

\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k

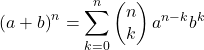
Of gelijkwaardig:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

De formule is een beetje ingewikkeld om het concept van de binomiaal van Newton te begrijpen, daarom hebben we hieronder de machten van binomialen van de laagste graad gepresenteerd, zodat je het beter kunt begrijpen:

formule voor de binominale stelling van Newton

Zoals je kunt zien, nemen bij het uitbreiden van een binomiaal de exponenten van de eerste term (a) af, terwijl de exponenten van de tweede term (b) toenemen , net zoals het lagere element van combinatorische getallen toeneemt.

Om de binomiale stelling te gebruiken, moet je daarom weten hoe je een combinatorisch getal moet oplossen, dat wil zeggen de algebraïsche uitdrukking van het type

\begin{pmatrix} 4 \\ 2 \end{pmatrix}

. Laten we dus, voordat we naar voorbeelden kijken van hoe je een binomiale Newton-berekening kunt berekenen, eerst de combinatorische getallen bekijken.

combinatorisch getal

Om een combinatorisch getal (of binomiale coëfficiënt) te bepalen, moet u de volgende formule toepassen:

\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}

Goud

n!

En

k!

Dit zijn faculteitsgetallen . Laten we ook onthouden dat een faculteitsgetal wordt berekend door alle positieve gehele getallen van 1 te vermenigvuldigen met dat getal:

n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n

Als voorbeeld zullen we een combinatorisch nummer vinden, zodat u kunt zien hoe het werkt:

\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4

Combinatorische getallen kunnen ook worden bepaald via de rekenmachine met de toets

\boxed{nCr}.

Binominale voorbeelden van Newton

Nu we weten wat de binominale stelling is, gaan we kijken hoe we de binomiale formule van Newton kunnen toepassen met behulp van twee numerieke voorbeelden.

voorbeeld 1

  • Pas de binomiaal van Newton toe om de macht van de volgende binomiaal te berekenen:

(x+3)^2

Aangezien deze binomiale kwadratuur kwadratisch is, kan deze uiteraard ook worden opgelost met de formules voor opmerkelijke identiteiten ( hoe opmerkelijke identiteiten op te lossen ), maar we zullen deze berekenen met de binominale stelling als voorbeeld.

Allereerst moeten we de binominale formule van Newton toepassen:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

In dit geval n=2, dus:

\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}

Kijk goed, in het begin verhogen we de eerste term (x) tot het maximaal mogelijke, wat in dit geval 2 is. Aan de andere kant verhogen we de tweede term (3) tot het minimaal mogelijke, wat altijd 0 is. naarmate we naar rechts gaan, moeten we de eerste term verhogen naar een lager getal dan voorheen en de tweede term naar een hoger getal dan voorheen.

Laten we nu de combinatorische getallen berekenen:

\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}

We lossen de machten op:

\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9

En ten slotte berekenen we de vermenigvuldigingen:

\left( x+3\right)^2 =x^2 + 6x + 9

Voorbeeld 2

Nu gaan we een iets moeilijker probleem oplossen.

  • Pas de binomiale formule van Newton toe om de macht van de volgende binomiale formule te vinden:

(2x+1)^3

De formule voor de binominale stelling is:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

In dit geval n=3, dus:

\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}

We berekenen de combinatorische getallen:

\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}

Nu gaan we de machten oplossen, hiervoor is het belangrijk dat je de volgende twee eigenschappen onthoudt:

• Wanneer een monomial wordt verhoogd naar een exponent, worden de coëfficiënt en de variabele verhoogd naar dezelfde exponent →

(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3

• Elke term die op 0 wordt gebracht, levert 1 → op

(2x)^0=1

We vinden daarom de krachten via deze 2 eigenschappen:

\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1

\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1

En ten slotte vermenigvuldigen we de termen:

\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1

De binominale driehoek van Newton en de driehoek van Tartaglia (of Pascal).

Zoals je in de bovenstaande voorbeelden hebt gezien, is het berekenen van combinatorische getallen een beetje vervelend. Daarom gaan we je een truc leren, zodat je geen combinatorische getallen hoeft op te lossen, omdat je direct kunt achterhalen hoeveel ze waard zijn met behulp van de Tartaglia-driehoek, ook wel de driehoek van Pascal genoemd.

Voor het geval je niet weet wat het is: de Tartaglia-driehoek , ook wel de driehoek van Pascal genoemd, is een wiskundige weergave van getallen gerangschikt in een driehoekige vorm.

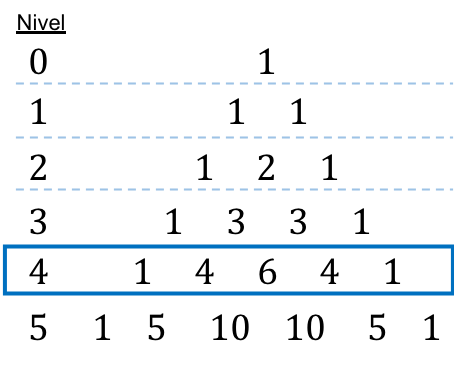
Om de Tartaglia- of Pascal-driehoek te construeren, moeten we beginnen bij de top van de driehoek, die altijd een 1 is, en vervolgens worden de nummers van de onderstaande lijnen bepaald. Elk getal in de volgende regels is gelijk aan de som van de twee getallen er direct boven, behalve de uiteinden van de regels die altijd 1 zijn.

Newton paar 1 middelbare school online

Elk van deze getallen in de Tartaglia-driehoek komt dus overeen met het resultaat van een combinatorisch getal, kijk naar de volgende afbeelding:

Bijvoorbeeld de binomiale coëfficiënt

\begin{pmatrix} 3 \\ 1 \end{pmatrix}

is gelijk aan 3, omdat er in de Tartaglia-driehoek een 3 op zijn plaats staat.

We kunnen daarom de driehoek van Tartaglia (of Pascal) gebruiken om de binomiaal van Newton veel sneller op te lossen, omdat het ons de berekeningen van combinatorische getallen bespaart.

Als we bijvoorbeeld de volgende potentiëring van een binomiaal willen uitvoeren:

(x+5)^3

Door de binominale regel van Newton toe te passen, verkrijgen we de volgende algebraïsche uitdrukking:

\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}

Welnu, in plaats van de combinatorische getallen één voor één te berekenen, kunnen we eenvoudig elk combinatorisch getal vervangen door de overeenkomstige coëfficiënt van de Tartaglia-driehoek. In dit geval wordt de binominale waarde verhoogd naar de 3e en komt daarom overeen met het derde niveau van de driehoek:

Tartaglia of de driehoek van Pascal en de binomiaal van Newton

\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}

En nu hoeven we alleen nog maar de resterende bewerkingen uit te voeren:

\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125

\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125

Zoals je kunt zien, wordt de driehoek van Tartaglia (of Pascal) gebruikt om de binomiaal van Newton op een eenvoudiger en snellere manier te berekenen, zoals we hebben laten zien. Daarom raden wij aan om het te gebruiken.

Om alles wat we tot nu toe hebben gezien samen te vatten, laten we een afbeelding achter die laat zien hoe de uitdrukkingen van de binomialen van Newton met de getallen van de Tartaglia (of Pascal) driehoek eruit zien:

De binomiaal van Newton en de driehoek van Pascal of Tartaglia

Negatieve Newton binomiaal: kracht van aftrekken

Tot nu toe zijn alle voorbeelden van de binominale waarde van Newton die we hebben opgelost toevoegingen geweest. Aan de andere kant, als een van de twee termen van de binominale term een negatief teken heeft, blijft de procedure vergelijkbaar, maar verandert er een beetje.

Wanneer een van de termen van de binominale waarde negatief is, dat wil zeggen dat het een aftrekking is van het type (ab) n , moeten de tekenen van de uitbreiding van de binomiale waarde van Newton elkaar afwisselen in de vorm + – + – + – + – …

Hieronder hebben we de machten van de negatieve binomials van de eerste 5 graden ontwikkeld met de binomiale stelling en met de coëfficiënten van de Tartaglia-driehoek al op hun plaats, zodat je direct de binomiale uitdrukking kunt vinden die je nodig hebt:

negatieve binomiale Newton-macht van een aftrekking 2

Eigenschappen van de binomiaal van Newton

De binominale uitdrukkingen van Newton hebben de volgende kenmerken:

  • Het ontbinden van de binomiale waarde van Newton resulteert altijd in één term meer dan de graad van de binominale waarde. Of met andere woorden, voor het paar

    (a+b)^n

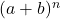
    ze worden beïnvloed

    n+1

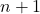
    voorwaarden.

  • De krachten van het element

    a

    Beginnen met

    n

    en ze nemen af totdat ze in het laatste kwartaal 0 bereikten.

  • De krachten van het element

    b

    ze gaan de andere kant op: ze beginnen bij 0 en nemen toe tot ze het bereiken

    n

    in de laatste termijn.

  • Voor elk element van de binominale waarde van Newton is de som van de exponenten van

    a

    En

    b

    is gelijk aan

    n.

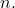
  • De coëfficiënt van de eerste term van de binomiale uitdrukking van Newton is altijd 1 (positief) en de tweede coëfficiënt is equivalent aan de exponent van de binomiale (positief of negatief).

Bereken de k-de term van de binomiaal van Newton

Hoewel dit ongebruikelijk is, kunnen we soms problemen tegenkomen waarbij ons, in plaats van de binomiale expansie van Newton uit te voeren, wordt gevraagd de k-de term van de binomiale expansie van Newton te bepalen, dat wil zeggen de term die de positie k inneemt.

Om dus de term te berekenen die de plaats k in de binomiaal van Newton inneemt, moeten we een formule gebruiken, die afhangt van het feit of de binominale waarde een optelling of een aftrekking is:

  • Als de binomiaal van Newton positief is, wordt de waarde van de k-de term berekend met de volgende formule:

(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

  • Als de binomiaal van Newton negatief is, wordt de waarde van de k-de term bepaald met de volgende formule:

(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

Als voorbeeld vinden we de vierde term van de volgende binomiaal van graad 5:

(x+3)^5

Omdat het een binomiaal is die uit een som bestaat, passen we de eerste formule toe:

T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

We vervangen de variabelen in de formule door hun overeenkomstige waarden:

T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}

En wij doen de bewerkingen:

T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}

T_4 = 10 \cdot x^{2}\cdot 27

T_4 = 270 x^{2}

En op deze manier hebben we de vierde term van de binominale expansie van Newton berekend zonder alle andere termen te hoeven berekenen.

Opgeloste oefeningen voor de binomiaal van Newton

Nu we hebben uitgelegd wat de binomiale stelling is, laten we je een aantal opgeloste stap-voor-stap oefeningen over de binominale stelling van Newton achter, zodat je kunt oefenen. Onthoud ook dat u vragen of suggesties voor ons kunt achterlaten in de reacties.

Oefening 1

Breid de volgende binominale macht uit met behulp van de binominale stelling:

(x+4)^3

We gebruiken eerst de binominale formule van Newton:

\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}

Omdat de binominale waarde wordt verheven tot de macht 3, kijken we naar het derde niveau van de Tartaglia-driehoek om direct de combinatorische getallen te vinden:

Oefeningen over de binominale stelling van Newton stap voor stap opgelost op de middelbare school

(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3

Wij voeren de bevoegdheden uit:

1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64

En tenslotte vermenigvuldigen we:

x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64

\bm{x^3 + 12x^2 + 48 x + 64}

Oefening 2

Bereken de volgende macht met de binominale formule van Newton:

(3x+2)^3

Eerst passen we de binominale formule van Newton toe:

\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}

Omdat de binominale kubus is gekubeerd, kijken we naar het derde niveau van de driehoek van Pascal om direct de waarden van de combinatorische getallen te kennen:

Oefeningen over de binominale stelling van Newton stap voor stap opgelost op de middelbare school

\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3

We berekenen de krachten van de monomialen:

1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8

En ten slotte doen we de vermenigvuldigingen:

27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8

\bm{27x^3 + 54x^2 +36x+8}

Oefening 3

Vouw de volgende polynoomuitdrukking uit met behulp van de binominale formule van Newton:

(2x-2)^3

Eerst gebruiken we de binominale formule van Newton. Maar aangezien we een aftrekking tussen de haakjes hebben, moeten we de tekens van de coëfficiënten van elke term afwisselen:

(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3

Omdat de binominale waarde wordt verheven tot de macht drie, kijken we naar het derde niveau van de Tartaglia-driehoek om de combinatorische getallen rechtstreeks te berekenen:

Oefeningen over de binominale stelling van Newton stap voor stap opgelost op de middelbare school

(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3

Wij voeren de bevoegdheden uit:

1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8

En we lossen de vermenigvuldigingen op:

8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8

\bm{8x^3 -24 x^2 +24x -8}

Oefening 4

Zoek de uitgebreide uitdrukking van de volgende binomiaal van Newton met de formule:

(4x-3y)^4

We moeten de algemene formule voor de binominale formule van Newton toepassen, maar omdat we in dit geval een aftrekking tussen haakjes hebben, moeten we de tekens van elke term afwisselen:

\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}

Omdat de binominale waarde naar de vierde wordt verhoogd, kijken we naar niveau 4 van de Tartaglia-driehoek om direct de combinatorische getallen te vinden:

De binomiale piramide van Newton

\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}

Wij realiseren alle bevoegdheden:

1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4

En ten slotte lossen we de vermenigvuldigingen op:

256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4

\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}

Oefening 5

Bepaal de zevende term in de uitbreiding van de volgende binomiale uitdrukking:

(2x-5y)^{10}

Omdat het een negatieve binomiaal is, moeten we de volgende formule gebruiken:

T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

We willen de term 7 bepalen en de binominale waarde wordt verheven tot de macht 10, dus door de waarden in de formule te vervangen wordt deze:

T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}

Het is daarom voldoende om te werken om de term te kennen:

\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}

Geschiedenis van de binomiaal van Newton

Hoewel de oorsprong van de binominale stelling wordt toegeschreven aan de beroemde Engelse wetenschapper Isaac Newton (1642-1727), werd de eerste formulering van de stelling in werkelijkheid rond het jaar 1000 voor het eerst ontdekt door de Perzische ingenieur Al-Karijí. En er werd zelfs ontdekt dat in de 13e eeuw kenden de Chinese wiskundigen Yang Hui en Chuh Shih-Chieh al binomiale uitbreidingen van kleine graden.

Later, in de 17e eeuw, bouwde Newton voort op de fundamenten die door eerdere wiskundigen waren gelegd om de binominale stelling uit te breiden. Met behulp van de interpolatie- en extrapolatiemethoden van wiskundige John Walls en de concepten van gegeneraliseerde exponenten kon hij een polynoomuitdrukking omzetten in een oneindige reeks.

Rond 1665 slaagde Newton erin aan te tonen dat de exponent n van de binomiale stelling ook een rationele exponent zou kunnen zijn, dat wil zeggen dat de macht van een binomiale ook kan worden opgelost als de exponent een breuk is. Aan de andere kant werd het ook bewezen in het geval van een negatieve exponent. En verrassend genoeg ontdekte hij dat de ontwikkelingen van de twee uitdrukkingen een oneindige reeks termen zijn.

Met deze ontdekking begon Newton de relatie tussen oneindige reeksen en eindige polynoomuitdrukkingen in twijfel te trekken, en concludeerde hij dat wiskundig gezien bewerkingen kunnen worden uitgevoerd met oneindige reeksen op dezelfde manier als eindige polynoomuitdrukkingen. Hoewel Newton deze stelling nooit heeft gepubliceerd, deed John Walls dat uiteindelijk in 1685, waarbij hij Newton de eer gaf voor deze ontdekking.

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven