▷ Wat is en hoe wordt een combinatorisch getal berekend (voorbeelden)

Op deze pagina leggen we uit wat een combinatorisch getal is en hoe het wordt berekend (formule). Bovendien kunt u voorbeelden zien van hoe u een combinatorisch getal kunt berekenen en oefenen met oefeningen die stap voor stap worden opgelost. We laten ook alle eigenschappen en toepassingen van combinatorische getallen zien. En tot slot leren we hoe we het resultaat van een combinatorisch getal rechtstreeks met de rekenmachine kunnen vinden.

Wat is een combinatorisch getal?

In de wiskunde is het combinatorische getal , ook wel de binomiale coëfficiënt genoemd, het aantal gewone combinaties (combinaties zonder herhaling) van groepen k elementen die kunnen worden gevormd uit een reeks van n elementen (n>k).

Een combinatorisch getal wordt als volgt tussen haakjes uitgedrukt:

$\begin{pmatrix}n \\ k \end{pmatrix}$

Aan de andere kant wordt het combinatorische getal n over k gelezen. Op dezelfde manier wordt n de teller genoemd en wordt k de orde genoemd.

Alleen al met de definitie van een combinatorisch getal is het moeilijk om de betekenis ervan te begrijpen. We zullen nu echter zien hoe het combinatorische getal wiskundig wordt bepaald, en daarna zullen we dieper ingaan op dit concept van combinatoriek. Je zult zien dat je het op deze manier beter zult begrijpen.

Combinatorische getalformule

De formule voor het berekenen van de waarde van een combinatorisch getal (of binomiale coëfficiënt) is als volgt:

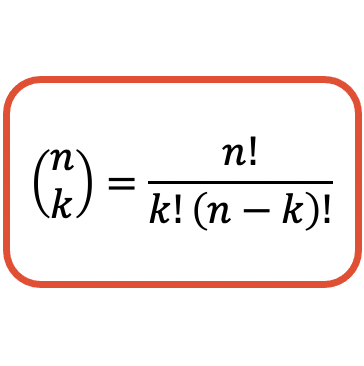
Bedenk dat in de algebra het uitroepteken overeenkomt met de faculteit van een getal. En om de faculteit van een getal te vinden, moet je alle positieve gehele getallen van 1 met dat getal vermenigvuldigen. Om bijvoorbeeld de faculteit van het getal 4 te berekenen, moet je 1, 2, 3 en 4 vermenigvuldigen:

$4! = 1\cdot 2 \cdot 3 \cdot 4 =24$

Het is ook belangrijk dat je weet dat de faculteit van 0 gelijk is aan 1.

$0! = 1$

Voorbeeld van het berekenen van een combinatorisch getal

Vervolgens gaan we als voorbeeld stap voor stap de waarde van een combinatorisch getal bepalen, zodat je kunt zien hoe het werkt:

Bereken de waarde van het combinatorische getal 5 gedeeld door 3.

De binomiale coëfficiënt van 5 gedeeld door 3 komt overeen met de volgende uitdrukking:

$\begin{pmatrix}5 \\ 3 \end{pmatrix}$

Als we de formule voor combinatorische getallen toepassen, moeten we daarom de volgende bewerkingen uitvoeren om de waarde ervan te bepalen:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!(5-3)!}$

Of gelijkwaardig:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{5!}{3!\cdot 2!}$

We vinden daarom de faculteiten:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{1\cdot 2 \cdot 3 \cdot 4 \cdot 5}{(1\cdot 2 \cdot 3) \cdot (1\cdot 2)}$

Vermenigvuldiging 1·2·3 wordt herhaald in de teller en de noemer, zodat de breuk vereenvoudigd kan worden door deze factor te elimineren:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{\cancel{1\cdot 2 \cdot 3} \cdot 4 \cdot 5}{(\cancel{1\cdot 2 \cdot 3)} \cdot (1\cdot 2)}$

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{ 4 \cdot 5}{1\cdot 2}$

Nu berekenen we de producten:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \cfrac{20}{2}$

En tenslotte maken we de verdeling:

$\begin{pmatrix}5 \\ 3 \end{pmatrix} = \bm{10}$

Eigenschappen van combinatorisch getal

Combinatorische getallen, of binomiale coëfficiënten, kunnen worden gecombineerd op basis van de volgende eigenschappen:

Twee complementaire combinatorische getallen zijn getallen die dezelfde teller n hebben en de som van hun orden is gelijk aan de genoemde teller. Het resultaat van twee complementaire combinatorische getallen is dus identiek.

$\begin{pmatrix}n \\ k \end{pmatrix} = \begin{pmatrix}n \\ n-k \end{pmatrix}$

Dit kenmerk van combinatorische getallen wordt ook wel symmetrie-identiteit genoemd.

6 gedeeld door 4 geeft bijvoorbeeld hetzelfde resultaat als 6 gedeeld door 2, omdat 6-4=2.

$\begin{pmatrix}6 \\ 4 \end{pmatrix} =\cfrac{6!}{4!(6-4)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(\cancel{1\cdot 2 \cdot 3\cdot 4})\cdot (1\cdot 2)}= \cfrac{30}{2} = \bm{15}$

$\begin{pmatrix}6 \\ 2 \end{pmatrix} =\cfrac{6!}{2!(6-2)!} = \cfrac{\cancel{1\cdot 2 \cdot 3\cdot 4}\cdot 5 \cdot 6}{(1\cdot 2)\cdot (\cancel{1\cdot 2 \cdot 3\cdot 4})}= \cfrac{30}{2} = \bm{15}$

De som van twee combinatorische getallen met dezelfde teller en opeenvolgende volgorden is gelijk aan een ander combinatorisch getal waarvan de teller gelijk is aan de teller van de optellingen plus 1 en waarvan de volgorde overeenkomt met de grootste waarde van de volgorden van de optellingen. Met andere woorden: er wordt altijd aan de volgende voorwaarde voldaan:

$\begin{pmatrix}n\\ k \end{pmatrix} + \begin{pmatrix}n\\ k+1 \end{pmatrix}= \begin{pmatrix}n+1\\ k+1 \end{pmatrix}$

Bijvoorbeeld:

$\begin{pmatrix}9\\ 2 \end{pmatrix} + \begin{pmatrix}9\\ 3 \end{pmatrix}= \begin{pmatrix}10\\ 3 \end{pmatrix}$

Deze eigenschap staat ook bekend als de regel van Pascal.

Aan de andere kant kan deze formule ook omgekeerd worden toegepast om een combinatorisch getal op te splitsen in twee eenvoudiger combinatorische getallen:

$\begin{pmatrix}n\\ k \end{pmatrix} = \begin{pmatrix}n-1\\ k-1 \end{pmatrix}+ \begin{pmatrix}n-1\\ k \end{pmatrix}$

Het combinatorische getal 8 gedeeld door 4 is bijvoorbeeld gelijk aan 7 gedeeld door 3 plus 7 gedeeld door 4:

$\begin{pmatrix}8\\ 4 \end{pmatrix} = \begin{pmatrix}7\\ 3 \end{pmatrix}+ \begin{pmatrix}7\\ 4 \end{pmatrix}$

Elk positief getal groter dan 1 is gelijk aan het getal zelf.

$\begin{pmatrix}n\\ 1 \end{pmatrix} =n$

De reden voor deze eigenschap is dat de faculteit van een getal gelijk is aan de faculteit van het vorige getal vermenigvuldigd met het getal zelf:

$\begin{pmatrix}n \\ 1 \end{pmatrix} =\cfrac{n!}{1!(n-1)!} = \cfrac{n\cdot (n-1) \cdot (n-2)\cdots 1}{(n-1) \cdot (n-2)\cdots 1}= n$

Voorbeelden van dit soort combinatorische getallen:

$\begin{pmatrix}12\\ 1 \end{pmatrix} =12 \qquad \begin{pmatrix}5\\ 1 \end{pmatrix} =5 \qquad \begin{pmatrix}9\\ 1 \end{pmatrix} =9$

Elk positief getal groter dan 0 is gelijk aan één.

$\begin{pmatrix}n\\ 0 \end{pmatrix} =1$

De noemer van de breuk van zo’n combinatorisch getal zal altijd gelijk zijn aan de teller van de breuk:

$\begin{pmatrix}n\\ 0 \end{pmatrix} =\cfrac{n!}{0!(n-0)!} =\cfrac{n!}{n!} = 1$

Voorbeelden van combinatorische getallen zoals deze:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}2\\ 0 \end{pmatrix} =1 \qquad \begin{pmatrix}23\\ 0 \end{pmatrix} =1$

Elk getal op zichzelf is gelijk aan 1.

$\begin{pmatrix}n\\ n \end{pmatrix} =1$

Hier is de demo:

$\begin{pmatrix}n\\ n \end{pmatrix} =\cfrac{n!}{n!(n-n)!} =\cfrac{n!}{n!\cdot 0!}= \cfrac{n!}{n!} = 1$

Voorbeelden van combinatorische getallen zoals deze:

$\begin{pmatrix}5\\ 5 \end{pmatrix} =1 \qquad \begin{pmatrix}37\\ 37 \end{pmatrix} =1 \qquad \begin{pmatrix}14\\ 14 \end{pmatrix} =1$

Een combinatorisch getal berekenen met de rekenmachine

Tot nu toe hebben we gezien hoe we een combinatorisch getal van min of meer eenvoudige getallen kunnen vinden, maar als we met zeer grote hoeveelheden moeten werken, is het beter om de rekenmachine te gebruiken om het combinatorische getal te bepalen. We zullen nu zien hoe u een combinatorisch getal in de rekenmachine kunt invoeren.

De sleutel die wordt gebruikt om een combinatorisch getal met de rekenmachine te berekenen, is dus de nCr-sleutel . En om de waarde van het combinatorische getal te bepalen, moet u eerst de teller van het combinatorische getal invoeren, vervolgens op de nCr-toets drukken, vervolgens de volgorde van het combinatorische getal invoeren en ten slotte op de gelijkheidstoets drukken.

$\begin{pmatrix}n\\ k \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} n \rightarrow \boxed{nCr} \rightarrow k \rightarrow \boxed{=}$

Op wetenschappelijke rekenmachines van CASIO heeft de nCr-toets meestal een eigen knop of bevindt deze zich boven de deelknop, afhankelijk van het model.

Als we bijvoorbeeld willen weten wat het combinatorische getal 10 gedeeld door 6 is, moeten we de volgende reeks uitvoeren:

$\begin{pmatrix}10\\ 6 \end{pmatrix}\quad \color{red}\bm{\longrightarrow} \quad \color{black} 10 \rightarrow \boxed{nCr} \rightarrow 6 \rightarrow \boxed{=} \rightarrow 210$

Toepassingen van combinatorisch getal

Als je zo ver bent gekomen, weet je waarschijnlijk al hoe je elk combinatorisch getal perfect kunt oplossen. Maar… waar wordt het combinatorische getal voor gebruikt? Welnu, dan zullen we alle voordelen zien die dit soort zeer speciale operaties met zich meebrengt.

Combinatoriek

Zoals we bovenaan de pagina zagen, het resultaat van een combinatorisch getal

$\begin{pmatrix}n\\ k \end{pmatrix}$

vertegenwoordigt het aantal mogelijke groepen van

$k$

elementen die kunnen worden gevormd uit een set van in totaal

$n$

artikelen.

Daarom kunnen sommige combinatorische problemen worden opgelost met behulp van combinatorische getallen (of binominale coëfficiënten). Laten we eens kijken hoe we dit kunnen doen aan de hand van een voorbeeld:

In een klas van 30 leerlingen willen we een groepje van 4 leerlingen kiezen om bepaalde taken uit te voeren. Wat is het totale aantal verschillende groepen dat gevormd kan worden?

In dit geval doet de volgorde van de leerlingen er niet toe, wordt dezelfde leerling niet twee keer herhaald binnen de groep en komen niet alle leerlingen in de groep. Daarom kan de combinatorische getalformule worden gebruikt om te bepalen op hoeveel manieren de groep kan worden gevormd.

Om dit te doen, moet u het combinatorische getal berekenen met het totale aantal studenten als teller en met het aantal studenten dat de groep zal vormen als volgorde:

$\begin{pmatrix}30 \\ 4 \end{pmatrix} =\cfrac{30!}{4!(30-4)!} =\cfrac{30\cdot 29 \cdot 28 \cdot 27 \cdot \cancel{26!}}{4\cdot 3 \cdot 2 \cdot 1 \cdot \cancel{26!}} = \cfrac{657720}{24}=\bm{27405}$

Het totaal aantal mogelijke combinaties bedraagt dus 27.405 groepen.

De binomiaal van Newton

Een andere toepassing van combinatorische getallen is de binomiaal van Newton. De binomiaal van Newton is een polynoom dat bestaat uit twee termen die samen tot een geheel getal zijn verheven, dat wil zeggen dat de binomiaal van Newton de polynoom is die reageert op de volgende algebraïsche uitdrukking:

$(a+b)^n$

Als de binominale kwadratuur is gekwadrateerd, betekent dit uiteraard dat het een opmerkelijke identiteit is en daarom gemakkelijk kan worden berekend met de overeenkomstige formule. Aan de andere kant, wanneer de binomiale waarde naar grote getallen wordt verhoogd, wordt de berekening behoorlijk moeilijk. Welnu, de binominale stelling van Newton zegt dat dit soort polynomen heel gemakkelijk kunnen worden berekend op basis van combinatorische getallen.

Klik op de volgende link en ontdek wat de binominale formule van Newton is en hoe deze wordt berekend. Daarnaast kun je voorbeelden zien en oefenen met oefeningen die stap voor stap worden opgelost. En tot slot zul je de merkwaardige geschiedenis van deze stelling ontdekken.

De driehoek van Tartaglia (of Pascal).

Zoals je in dit artikel hebt gezien, kan het handmatig berekenen van de binomiale coëfficiënt van grote getallen omslachtig en ingewikkeld zijn.

Aan de andere kant kunnen met de Tartaglia-driehoek, ook wel de driehoek van Pascal genoemd, alle combinatorische getallen eenvoudig worden bepaald met behulp van een geheugensteuntje. Dit is logischerwijs erg handig omdat het veel tijd bespaart tijdens de berekeningen.

Om erachter te komen hoe je dit precies moet doen, zie de driehoeksverklaring van Tartaglia . Op deze gelinkte pagina ontdek je wat deze mysterieuze driehoek is, waarvoor hij wordt gebruikt (hij heeft verrassende toepassingen) 😮 en wat zijn oorsprong is (hij werd al meer dan 1000 jaar geleden gebruikt).

Combinatorische getaloefeningen opgelost

Zodat u de uitgelegde concepten kunt oefenen en volledig kunt begrijpen, laten we u verschillende oefeningen stap voor stap oplossen over combinatorische getallen.

Oefening 1

Zoek het combinatorische getal 9 bij 5 (zonder een rekenmachine te gebruiken).

Zie de oplossing

Om de waarde van het combinatorische getal 9 van de 5 te vinden, passen we eenvoudigweg de factoriële formule toe:

$\begin{pmatrix}9 \\ 5 \end{pmatrix} =\cfrac{9!}{5!(9-5)!} = \cfrac{9\cdot 8 \cdot 7\cdot 6\cdot \cancel{5!}}{\cancel{5!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{3024}{24} = \bm{126}$

Oefening 2

Wat is het resultaat van de volgende som van twee combinatorische getallen? (zonder rekenmachine)

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}$

Zie de oplossing

Uit de eigenschappen van combinatorische getallen volgt dat de som van het probleem gelijk is aan het volgende combinatorische getal:

$\begin{pmatrix}10\\ 6 \end{pmatrix} + \begin{pmatrix}10\\ 7 \end{pmatrix}=\begin{pmatrix}11\\ 7 \end{pmatrix}$

Daarom is het voldoende om het combinatorische getal 11 van de 7 te berekenen:

$\begin{pmatrix}11 \\ 7 \end{pmatrix} =\cfrac{11!}{7!(11-7)!} = \cfrac{11\cdot 10 \cdot 9\cdot 8 \cdot \cancel{7!}}{\cancel{7!} \cdot (4 \cdot 3 \cdot 2 \cdot 1)}= \cfrac{7920}{24} = \bm{330}$

Oefening 3

Bepaal of de volgende combinatorische getallen gelijk zijn:

$\begin{pmatrix}6\\ 0 \end{pmatrix} \qquad \begin{pmatrix}6\\ 1 \end{pmatrix}\qquad \begin{pmatrix}6\\ 6 \end{pmatrix}$

Zie de oplossing

Om het resultaat van de drie combinatorische getallen te vinden, hoeft u geen rekenmachine te gebruiken, maar ze kunnen gemakkelijk worden gevonden dankzij de eigenschappen van combinatorische getallen.

Allereerst geeft een combinatorisch getal van elk getal groter dan 0 1. Daarom:

$\begin{pmatrix}6\\ 0 \end{pmatrix} =1$

Aan de andere kant is elk getal groter dan één gelijk aan het getal zelf. Nog:

$\begin{pmatrix}6\\ 1 \end{pmatrix} =6$

En ten slotte is elk combinatorisch getal dat wordt gevormd door hetzelfde getal dat twee keer wordt herhaald, gelijk aan 1. Dus:

$\begin{pmatrix}6\\ 6 \end{pmatrix} =1$

Concluderend zijn de eerste en derde combinatorische getallen in het probleem gelijk, maar ze verschillen van het middelste combinatorische getal.

$\begin{pmatrix}6\\ 0 \end{pmatrix}= \begin{pmatrix}6\\ 6 \end{pmatrix}\neq \begin{pmatrix}6\\ 1 \end{pmatrix}$

Combinatorisch getal (of binomiale coëfficiënt)

Wat is een combinatorisch getal?

Combinatorische getalformule

Voorbeeld van het berekenen van een combinatorisch getal

Eigenschappen van combinatorisch getal

Een combinatorisch getal berekenen met de rekenmachine

Toepassingen van combinatorisch getal

Combinatoriek

De binomiaal van Newton

De driehoek van Tartaglia (of Pascal).

Combinatorische getaloefeningen opgelost

Oefening 1

Oefening 2

Oefening 3

Laat een reactie achter Reactie annuleren