Op deze pagina leest u wat het is en hoe u de numerieke waarde van een polynoom kunt berekenen. Bovendien kunt u stap voor stap opgeloste voorbeelden en oefeningen zien van de numerieke waarde van een polynoom.
Wat is de numerieke waarde van een polynoom?
In de wiskunde is de numerieke waarde van een polynoom P(x) voor de waarde x=a, dat wil zeggen P(a), het resultaat dat wordt verkregen door de variabele x van de polynoom te vervangen door het getal a en de aangegeven berekeningen uit te voeren. in de polynoomuitdrukking.
Om u het concept van de numerieke waarde van een polynoom beter te laten begrijpen, laten we hieronder met een voorbeeld zien hoe deze wordt berekend:
Hoe de numerieke waarde van een polynoom te berekenen
Nu we de wiskundige definitie van de numerieke waarde van een polynoom kennen, gaan we kijken hoe we de numerieke waarde van een polynoom kunnen bepalen aan de hand van een voorbeeld:
- Wat is de numerieke waarde van de volgende polynoom voor x=2?
![]()
Om de numerieke waarde van de polynoom te vinden, is het noodzakelijk om de genoemde polynoom te evalueren in de waarde die door het probleem wordt gegeven, dat wil zeggen dat het noodzakelijk is om de variabele te vervangen
![]()
van de polynoom door de waarde van de uitspraak. Daarom moeten we in dit geval de letter vervangen
![]()
Voor 2:
![]()
En zodra we de waarde in de algebraïsche uitdrukking van de polynoom hebben vervangen, voeren we de bewerkingen uit. Dus lossen we eerst de machten op:
![]()
Nu berekenen we de vermenigvuldigingen:
![]()
En ten slotte voegen we de termen toe en trekken ze af:
![]()
Concluderend is de numerieke waarde van de polynoom voor x=2 gelijk aan 21.
Zoals u kunt zien, is het vinden van de numerieke waarde van een polynoom niet erg ingewikkeld, maar er zijn wel enkele zeer nuttige toepassingen voor. Weten hoe je de numerieke waarde van een polynoom kunt vinden, is bijvoorbeeld essentieel om de reststelling te kunnen gebruiken, een zeer belangrijke stelling over polynomen. Klik op deze link en ontdek wat de reststelling is , je vindt de uitleg, gebruiksvoorbeelden en oefeningen stap voor stap opgelost.
Voorbeelden van numerieke waarden van veeltermen
Zodat u begrijpt hoe u de numerieke waarde van een polynoom kunt verkrijgen, laten we u andere opgeloste voorbeelden achter:
voorbeeld 1
- Bereken de numerieke waarde van de polynoom
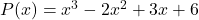
Voor

![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3293713c5e12fac56d94be90f6bfc6e5_l3.png)
In dit geval is de numerieke waarde van de polynoom gelijk aan 0. Dit heeft consequenties vanwege de eigenschappen van polynomen, aangezien we dankzij de factorstelling kunnen weten wat de rest van bepaalde delingen tussen polynomen zal zijn. Voor meer informatie klikt u op de vorige link, waar we uitleggen wat deze stelling is en waarvoor deze dient.
Voorbeeld 2
- Bepaal de numerieke waarde van de polynoom
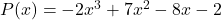
Voor
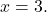
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8b1145d569157b4e771adfae674e2c_l3.png)
Tot nu toe hebben we alleen gezien hoe je de numerieke waarde van een polynoom op de klassieke manier kunt bepalen, maar je moet weten dat er een andere methode is. Meer specifiek kun je de numerieke waarde van een polynoom ook berekenen met de Ruffini-methode . U moet ook weten hoe u deze procedure moet gebruiken, dus we raden u aan de gedetailleerde uitleg in de link te bekijken.
Numerieke waarde van een polynoom met twee of meer variabelen
We hebben zojuist gezien hoe we de numerieke waarde van een polynoom kunnen vinden als deze slechts één variabele heeft. Maar… hoe krijg je de numerieke waarde van een polynoom als deze meer dan één variabele heeft?
Welnu, als een polynoom twee of meer letters heeft, moet de numerieke waarde ervan op dezelfde manier worden berekend, dwz eerst elke variabele in de polynoom vervangen door de overeenkomstige waarde en vervolgens de polynoombewerkingen oplossen .
Hieronder ziet u bijvoorbeeld een probleem van dit type opgelost:
- Zoek de numerieke waarde van de multivariate polynoom
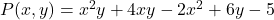
voor de waarden
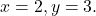
Eerst vervangen we elke variabele door de bijbehorende waarde, dwz we vervangen de letter
![]()
voor 2 en we veranderen de letter
![]()
door 3:
![]()
We lossen de machten op:
![]()
Nu berekenen we de producten:
![]()
En tot slot doen we de optellingen en aftrekkingen:
![]()
De numerieke waarde van de polynoom voor de instructiegegevens is dus gelijk aan 41.
Opgeloste oefeningen over de numerieke waarde van een polynoom
Oefening 1
Wat is de numerieke waarde van de polynoom P(x) voor x=-2?
![]()
Om de numerieke waarde van de polynoom te vinden, hoeven we alleen maar de waarde uit de verklaring in de polynoomuitdrukking te vervangen en de resulterende bewerkingen op te lossen:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-93b7cf1a6c7e930a0a70fc8302f4012d_l3.png)
Oefening 2
Bereken de numerieke waarde van het volgende polynoom met breuken voor x=4.
![]()
Ongeacht of de polynoom breuken heeft of niet, de procedure voor het vinden van de numerieke waarde van de polynoom is altijd hetzelfde. We moeten daarom de variabele x vervangen door 4 en de berekeningen oplossen:
![Rendered by QuickLaTeX.com \begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04fa4389b5e7c5257937ad35aed07c7b_l3.png)
Oefening 3
Bepaal de numerieke waarde van de polynoom voor de waarden x=3, y=5 en z=-2
![]()
Om de numerieke waarde van de multivariate polynoom te bepalen, volstaat het om de in het probleem gegeven waarden in de algebraïsche uitdrukking te vervangen en de resulterende bewerkingen op te lossen:
![Rendered by QuickLaTeX.com \begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29683a91c14427a8ea42c3518e59e53f_l3.png)
Oefening 4
Gegeven de polynoom
![]()
parameterwaarde berekenen
![]()
zodat
![]()
In dit probleem, om de waarde van het onbekende te vinden
![]()
we moeten de vergelijking oplossen
![]()
![]()
Daarom proberen we eerst de waarde van P(-2) te berekenen:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b58398099c8033b93a559e2f0c87f1a_l3.png)
Nu maken we de verkregen uitdrukking gelijk aan 5:
![]()
![]()
En ten slotte lossen we de resulterende vergelijking op:
![]()
![]()