Algebraïsche breuken: vereenvoudiging, bewerkingen, opgeloste oefeningen,…

Op deze pagina leggen we uit wat algebraïsche breuken zijn, wanneer ze gelijkwaardig zijn, hoe je ze kunt vereenvoudigen en hoe je bewerkingen met algebraïsche breuken kunt uitvoeren (optellen, aftrekken, vermenigvuldigen en delen). Bovendien kunt u opgeloste stapsgewijze oefeningen voor algebraïsche breuken bekijken. Kortom, hier vind je alles over algebraïsche breuken.

Wat zijn algebraïsche breuken?

In de wiskunde is een algebraïsche breuk een breuk met een polynoom in de teller en een andere polynoom in de noemer.

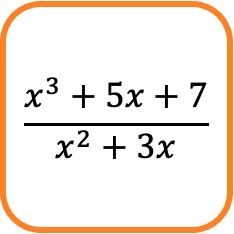
De bovenstaande breukuitdrukking bestaat bijvoorbeeld uit een algebraïsche breuk omdat de teller en de noemer uit polynomen bestaan.

Algebraïsch breukequivalent

Als we eenmaal de definitie van algebraïsche breuken kennen, gaan we kijken wanneer twee van zulke breuken gelijk zijn.

Wiskundig gezien zijn twee algebraïsche breuken gelijkwaardig als aan de volgende voorwaarde wordt voldaan:

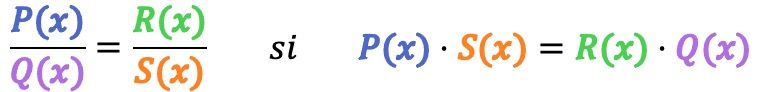
Als voorbeeld zullen we controleren of de volgende 2 algebraïsche breuken equivalent zijn:

Om te bepalen of breuken algebraïsch gelijk zijn, vermenigvuldigen we hun termen transversaal:

Laten we nu de vermenigvuldigingen van polynomen berekenen:

We hebben dezelfde uitdrukking aan beide kanten van de vergelijking, dus het zijn in feite twee equivalente algebraïsche breuken.

Vereenvoudig algebraïsche breuken

Om een algebraïsche breuk te vereenvoudigen, moet je eerst de polynomen in de teller en de noemer ontbinden en vervolgens de factoren die ze gemeen hebben elimineren.

Om algebraïsche breuken te vereenvoudigen, is het uiteraard essentieel dat u weet wat polynoomontbinden is en hoe dit wordt gedaan. Als u nog steeds niet weet hoe polynomen in factoren worden verwerkt of als u het zich niet helemaal herinnert, raad ik u aan eerst naar de gelinkte pagina te gaan voordat u verdergaat, anders begrijpt u de procedure nauwelijks. Er wordt stap voor stap uitgelegd hoe je polynomen ontbindt en daarnaast kun je verschillende voorbeelden bekijken en oefenen met opgeloste oefeningen.

Laten we nu eens kijken hoe een algebraïsche breuk wordt vereenvoudigd door de methode voor het ontbinden van polynomen toe te passen aan de hand van een voorbeeld:

• Vereenvoudig de volgende algebraïsche breuk:

Eerst ontbinden we de polynomen van de teller en de noemer van de breuk:

⬆(Als je niet weet hoe polynomen in factoren zijn verwerkt, kijk dan eens naar de bovenstaande link)⬆

En zodra we de polynomen hebben ontbonden, elimineren we de gemeenschappelijke factoren tussen de teller en de noemer, dat wil zeggen dat we alle termen verwijderen die worden herhaald:

De vereenvoudigde algebraïsche breuk ziet er daarom als volgt uit:

In dit probleem werden de polynomen van de algebraïsche breuk in rekening gebracht door hun wortels te vinden; Soms kan een polynoom echter rechtstreeks worden ontbonden door de gemeenschappelijke factor te nemen (veel snellere methode). In deze link ziet u wat het betekent om een gemeenschappelijke factor uit een polynoom te nemen en ontdekt u hoe u een algebraïsche breuk kunt vereenvoudigen met behulp van een gemeenschappelijke factor.

Bewerkingen met algebraïsche breuken

Zoals elk type breuk kunnen bewerkingen ook worden uitgevoerd met algebraïsche breuken. Concreet kunnen algebraïsche breuken worden opgeteld, afgetrokken, vermenigvuldigd en verdeeld. Hieronder leggen we stap voor stap aan de hand van voorbeelden uit hoe elk type handeling wordt berekend.

Optellen en aftrekken van algebraïsche breuken

De procedure voor het optellen en aftrekken van algebraïsche breuken is vrijwel identiek, dus we zullen ze samen analyseren. Eerst zullen we een voorbeeld zien van twee toegevoegde algebraïsche breuken, en hieronder zullen we het verschil bestuderen tussen de methode voor het aftrekken van algebraïsche breuken.

Algebraïsche breuken optellen

Het optellen van algebraïsche breuken gaat op dezelfde manier als bij normale breuken: eerst reduceer je de breuken tot een gemeenschappelijke noemer en tel je vervolgens de tellers op.

Laten we eens kijken hoe algebraïsche breuken worden toegevoegd aan de hand van een voorbeeld:

We ontbinden eerst de noemers van de breuken:

We moeten nu de lcm (kleinste gemene veelvoud) van de noemers vinden om de breuken tot een gemeenschappelijke noemer te herleiden.

Tip: de lcm van de noemers wordt altijd gevormd uit het product van de factoren die ze gemeenschappelijk hebben, verhoogd tot de grootste exponent vermenigvuldigd met de niet-gemeenschappelijke factoren .

In ons geval bijvoorbeeld

De gemeenschappelijke deler tussen de noemers tot de grootste exponent is

En de niet-gemeenschappelijke factor tussen de noemers is

Daarom is de lcm van de noemers in dit geval:

De lcm van de noemers is dus

dit wordt dus de nieuwe noemer van de 2 breuken.

Zodra we de gemeenschappelijke noemer hebben gevonden, moeten we de tellers wijzigen. Om dit te doen, volgen we hetzelfde proces als voor het optellen van normale breuken: voor elke breuk delen we de lcm

tussen de oorspronkelijke noemer en vermenigvuldig het resultaat met de teller:

Dus nu kunnen we de twee breuken samenvoegen omdat ze dezelfde noemer hebben:

Ten slotte werken we met de teller. We doen eerst het product van de monomial en de polynoom:

Vervolgens voegen we de vergelijkbare termen toe aan de teller:

Normaal gesproken zouden we er al zijn, maar als we dit probleem van dichtbij bekijken, kunnen we de algebraïsche breuk nog verder vereenvoudigen door een gemeenschappelijke factor uit de teller te verwijderen. Nog:

En dus hebben we de som van de twee algebraïsche breuken al voltooid.

Aftrekken van algebraïsche breuken

Om algebraïsche breuken af te trekken, moeten we een soortgelijke procedure volgen als het optellen van algebraïsche breuken: eerst reduceren we de breuken tot een gemeenschappelijke noemer, en trekken dan de tellers af.

Laten we eens kijken hoe algebraïsche breuken worden afgetrokken met een voorbeeld:

Eerst moeten we de noemers van de twee breuken ontbinden:

Net als bij het aftrekken van normale breuken moeten we nu de lcm (kleinste gemene veelvoud) van de noemers berekenen om de breuken tot een gemeenschappelijke noemer te herleiden. In dit geval is de lcm van de noemers gelijk

dit wordt dus de nieuwe noemer van de 2 breuken.

Nu passen we hetzelfde proces toe als voor het aftrekken van normale breuken: voor elke breuk delen we de lcm

tussen de oorspronkelijke noemer en vermenigvuldig het resultaat met de teller:

We voegen nu de twee algebraïsche breuken samen, omdat ze dezelfde noemer hebben:

En we werken met de teller. We lossen eerst de polynomiale vermenigvuldigingen op:

Een veel voorkomende fout bij het aftrekken van algebraïsche breuken is het vergeten haakjes te plaatsen na het uitvoeren van deze vermenigvuldiging. Dit zou een fout zijn, aangezien het negatieve teken alle resulterende elementen van het product beïnvloedt, en niet alleen de eerste term.

We voeren de bewerkingen tussen haakjes uit:

Dankzij het minteken veranderen we dus het teken van alle termen tussen haakjes:

En ten slotte groeperen we soortgelijke monomialen:

Vermenigvuldiging van algebraïsche breuken

Om algebraïsche breuken te vermenigvuldigen, ontbinden we eerst alle polynomen van genoemde breuken, vermenigvuldigen we vervolgens de tellers met elkaar en de noemers met elkaar, en tenslotte vereenvoudigen we de verkregen breuk.

Daarom wordt het product van algebraïsche breuken feitelijk op dezelfde manier berekend als het product van normale breuken.

Laten we vervolgens eens kijken hoe we twee algebraïsche breuken kunnen vermenigvuldigen met een voorbeeld:

Allereerst moet je alle polynomen van de breuken ontbinden, zowel de tellers als de noemers:

Laten we nu breuken vermenigvuldigen. Om dit te doen, vermenigvuldigen we de tellers en noemers met elkaar:

En ten slotte vereenvoudigen we de factoren die worden herhaald in de noemer en de teller:

Het resultaat van de vermenigvuldiging is dus:

De breuk kan niet verder worden vereenvoudigd. We zijn dus al klaar met het vermenigvuldigen van algebraïsche breuken.

Verdeling van algebraïsche breuken

Om een deling van algebraïsche breuken te berekenen, ontbinden we eerst alle polynomen in factoren, vervolgens vermenigvuldigen we de breuken transversaal (de eerste teller met de tweede noemer en de eerste noemer met de tweede teller) en tenslotte vereenvoudigen we de algebraïsche breuk.

Laten we dus beter zien hoe twee algebraïsche breuken worden verdeeld aan de hand van een voorbeeld:

De eerste stap bij het delen van twee algebraïsche breuken is het ontbinden van alle polynomen die bij de bewerking betrokken zijn:

Nu moeten we de breuken delen. Om dit te doen, vermenigvuldigen we de breuken transversaal, dat wil zeggen dat de eerste teller wordt vermenigvuldigd met de tweede noemer en het resultaat zal de teller van de nieuwe breuk zijn, en op dezelfde manier wordt de eerste noemer vermenigvuldigd met de tweede teller. en het resultaat is de noemer van de nieuwe breuk:

We vereenvoudigen de factoren die worden herhaald in de noemer en de teller:

En sindsdien kunnen we de breuk nog verder vereenvoudigen

De breuk kan niet verder worden vereenvoudigd. Daarom hebben we algebraïsche breuken al verdeeld.

Opgeloste oefeningen over algebraïsche breuken

Hieronder bieden we u verschillende oefeningen aan die stap voor stap zijn opgelost met betrekking tot algebraïsche breuken, zodat u kunt oefenen en zo het concept kunt begrijpen. Vergeet niet dat je ons al je vragen hieronder in de reacties kunt stellen! 💬💬💬

Oefening 1

Bepaal of de volgende algebraïsche breuken al dan niet equivalent zijn:

Om te controleren of twee algebraïsche breuken equivalent zijn, moet je ze transversaal vermenigvuldigen en kijken of je een gelijkheid verkrijgt. We zullen dus eerst de eerste en tweede breuk controleren:

We lossen de opmerkelijke identiteit aan de linkerkant van de vergelijking op:

✅

In dit geval hebben we een gelijkheid verkregen, dus de eerste en tweede breuk zijn algebraïsch gelijk.

We passen nu dezelfde procedure toe met de eerste en derde algebraïsche breuk:

❌

Deze keer voldoen de algebraïsche breuken echter niet aan de vergelijking, dus zijn de eerste en derde breuk wiskundig verschillend.

Concluderend is de derde breuk verschillend van de eerste breuk en daarom ook ongelijk aan de tweede breuk, aangezien de eerste en tweede breuk gelijkwaardig zijn.

Oefening 2

Vereenvoudig de volgende algebraïsche breuken:

Om een algebraïsche breuk te vereenvoudigen, moeten we de polynomen in de teller en de noemer ontbinden en vervolgens de herhaalde factoren elimineren. Nog:

Oefening 3

Bereken de volgende optellingen en aftrekkingen van algebraïsche breuken:

Om algebraïsche breuken op te tellen (of af te trekken), moeten we eerst de breuken reduceren tot een gemeenschappelijke noemer en vervolgens de tellers optellen (of aftrekken). DUS:

Oefening 4

Los de volgende vermenigvuldigingen en delingen van algebraïsche breuken op:

Om algebraïsche breuken te vermenigvuldigen, moeten we eerst alle veeltermen ontbinden in factoren, vervolgens de tellers en noemers met elkaar vermenigvuldigen en ten slotte de resulterende breuk vereenvoudigen.

Aan de andere kant, om algebraïsche breuken te delen, ontbinden we eerst alle veeltermen, vermenigvuldigen we vervolgens de breuken transversaal (de eerste teller met de tweede noemer en de eerste noemer met de tweede teller) en tenslotte vereenvoudigen we de gevonden algebraïsche breuk.

Wat vind jij van de uitleg? Vond je het leuk? Of heeft u suggesties? 💬 Vertel ons wat je van deze pagina vindt in de reacties! Wij lezen jullie allemaal! 👀 En vergeet niet dat je ook al je vragen aan ons kunt stellen! ❔👇❔👇