Polynomen ontbinden in factoren (polynomiale factoring)

Op deze pagina leggen we uit hoe u elk type polynoom kunt ontbinden. We zullen eerst zien hoe we een polynoom ontbinden in factoren met de regel van Ruffini, daarna gaan we verder met hoe polynomen zonder onafhankelijke term worden ontbonden, daarna analyseren we de factorisaties van wortelpolynomen met breuken en ten slotte de speciale gevallen van factorisaties (opmerkelijke identiteiten, factorisatie door groepering, trinomialen, enz.). Alle uitleg wordt gegeven met voorbeelden en bovendien kun je aan het einde oefenen met de stap voor stap opgeloste oefeningen om veeltermen in factoren te ontbinden.

Wat is polynomiale factorisatie?

Polynoomfactorisatie is een techniek die in de wiskunde wordt gebruikt om een polynoom te ontbinden in het product van factoren.

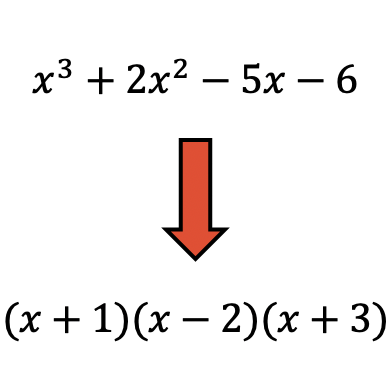
Het ontbinden van polynomen in factoren is erg handig omdat het gemakkelijker is om bewerkingen uit te voeren met polynomen die in factoren zijn verwerkt.

Nu we weten wat polynoomontbinden is, gaan we kijken hoe polynomen worden ontbonden.

Hoe polynomen te ontbinden met de regel van Ruffini

Om te begrijpen hoe je een polynoom kunt factoriseren met de regel van Ruffini, moet je uiteraard eerst weten hoe je de regel van Ruffini moet toepassen . Daarom laten we u deze link achter voor het geval u eerst wilt bekijken hoe de procedure eruit zag.

Om een polynoom in factoren te ontbinden, moeten de volgende stappen worden gevolgd:

1. De wortels van de polynoom worden berekend volgens de regel van Ruffini.
2. Elke gevonden wortel van het type x=a wordt uitgedrukt in de vorm van een factor (xa).
3. De in factoren verwerkte polynoom is het product van alle gevonden factoren, vermenigvuldigd met de coëfficiënt van de term van de hoogste graad van de ongewogen polynoom.

Om u te laten zien hoe dit in zijn werk gaat en de procedure voor het ontbinden van polynomen beter te begrijpen, vindt u hieronder een concreet voorbeeld dat stap voor stap wordt uitgelegd:

• Factor de volgende polynoom:

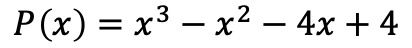
Het eerste dat u moet doen, is de wortels of nulpunten van de polynoom berekenen. Om dit te doen, moeten we de delers van de onafhankelijke term van de polynoom vinden, die in dit geval ±1, ±2 en ±4 zijn.

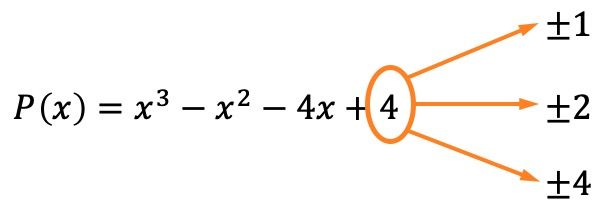
Nu weten we, dankzij de rest- en factorenstelling, dat als de rest van de deling van de polynoom door een van deze waarden gelijk is aan 0, dit betekent dat die waarde een wortel is van de polynoom.

We moeten daarom de polynoom delen door elk van de delers van de onafhankelijke term met de regel van Ruffini en kijken in welke gevallen de rest nul is.

We beginnen bijvoorbeeld met het toepassen van de regel van Ruffini met

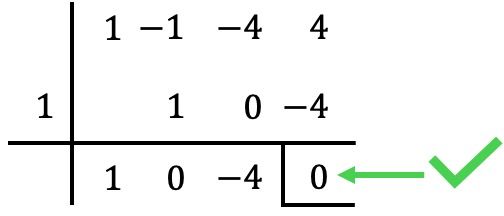
In dit geval is de rest (of residu) van de deling dus nul

Het is een wortel van de polynoom. ✅

Perfect, we hebben al een wortel van de polynoom, het enige dat overblijft is het bepalen van de andere resterende wortels. Om dit te doen, gebruiken we bijvoorbeeld de regel van Ruffini met een andere deler van de onafhankelijke term

Het is ook niet nodig om de methode van Ruffini te gebruiken met de gehele polynoom, maar we kunnen doorgaan waar we gebleven waren in de vorige stap:

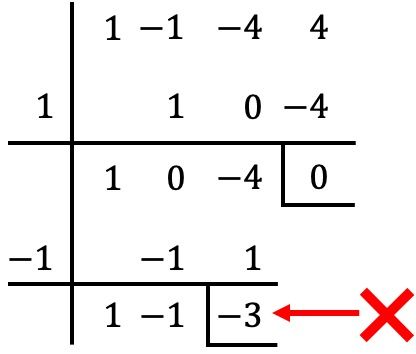
In dit geval echter bij het delen door

de verkregen rest is verschillend van 0, dus

Het is geen wortel van de polynoom. ❌

We moeten daarom een andere waarde proberen, we doen bijvoorbeeld de Ruffini-regel

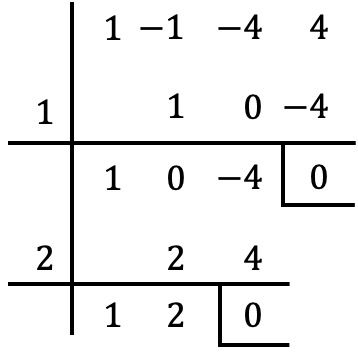
In dit geval krijgen we opnieuw een restant van nul, dus

Het is ook een wortel van de polynoom.

En we blijven dezelfde procedure toepassen. Nu controleren we of

is het een wortel van de polynoom of niet:

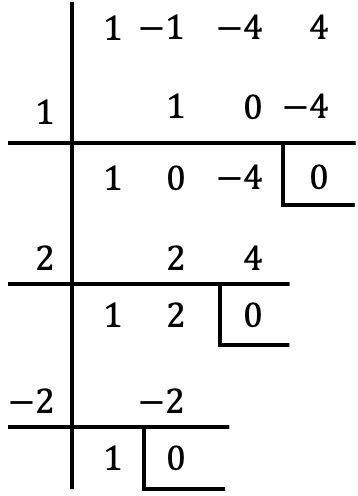
Door te delen door

Met de regel van Ruffini verkrijgen we dus een restant van nul

is een wortel of nul van de polynoom.

We kunnen de regel van Ruffini dus niet langer blijven toepassen, we hebben dus al alle wortels van de polynoom gevonden, namelijk:

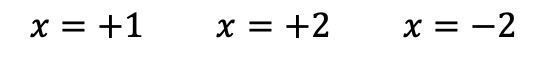
Zodra we alle wortels van de polynoom hebben bepaald, kunnen we deze ontbinden in factoren. Om dit te doen, drukt u eenvoudigweg elke wortel uit

in de vorm van een factor van het type

, dat wil zeggen dat je voor elke wortel een haakje met a moet plaatsen

en de wortel is van teken veranderd:

En nu we alle wortels hebben uitgedrukt als factoren, moeten we alle haakjes vermenigvuldigen met de coëfficiënt van de term van de hoogste graad van de oorspronkelijke polynoom:

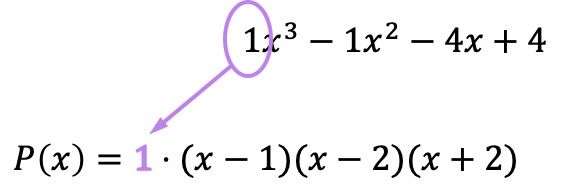
Hoewel in dit geval de coëfficiënt 1 is en dus geen invloed heeft op het resultaat, is het belangrijk om te onthouden dat u deze vermenigvuldiging moet uitvoeren. Als de coëfficiënt anders was dan 1, zou de in factoren verwerkte polynoom veranderen en daarom zouden we, door het getal niet in te voeren, een fout maken bij het ontbinden van de polynoom.

Kort gezegd is het gefactoriseerde polynoom:

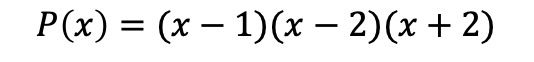
Veeltermen ontbinden in factoren zonder onafhankelijke term

We hebben zojuist gezien dat de onafhankelijke term belangrijk is voor het ontbinden van polynomen, omdat we hierdoor de mogelijke wortels van de polynoom kunnen identificeren. Maar hoe ontbind je een polynoom dat geen onafhankelijke term heeft?

Om een polynoom zonder een onafhankelijke term in factoren te ontbinden , moet je eerst de gemeenschappelijke factor van het polynoom extraheren en vervolgens de wortels van het polynoom zonder de gemeenschappelijke factor extraheren met behulp van de regel van Ruffini.

Als je het zo schrijft, klinkt het misschien een beetje ingewikkeld, dus laten we stap voor stap een voorbeeld oplossen, zodat je kunt zien hoe je een polynoom ontbindt in factoren met een gemeenschappelijke factor:

• Voer de factoriële ontleding uit van de volgende polynoom:

Zoals je kunt zien heeft de polynoom in het probleem geen onafhankelijke term, dus moeten we de gemeenschappelijke factor van de polynoom nemen. Als we goed kijken, hebben alle elementen van de polynoom er minstens één

dus de gemeenschappelijke factor is

Wanneer we de gemeenschappelijke factor uit de polynoom extraheren, krijgen we daarom de volgende uitdrukking:

En zodra we de gemeenschappelijke factor van de polynoom hebben geëxtraheerd, passen we de regel van Ruffini toe om de wortels van de polynoom tussen haakjes te berekenen (met de procedure die we in de vorige sectie hebben gezien):

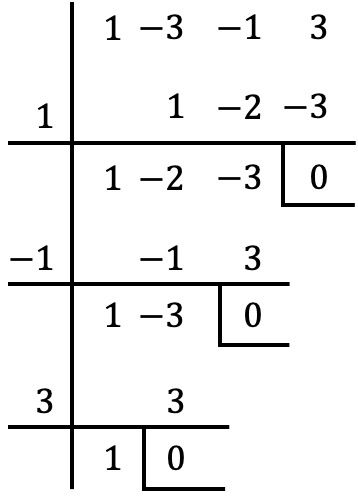
Dus de wortels of nullen van de polynoom tussen haakjes zijn:

Om de polynoom in factoren te ontbinden, vervangt u daarom eenvoudigweg de polynoom tussen haakjes door de wortels in factorvorm (zoals uitgelegd in het gedeelte hierboven):

En op deze manier hebben we de polynoom al in factoren ontbonden die geen term van graad 0 had. Merk op dat het enige verschil is dat we eerst een gemeenschappelijke factor moeten extraheren, maar alle volgende stappen zijn precies hetzelfde.

Aan de andere kant moet je dat weten

Het is ook een wortel van de polynoom, want als we de gemeenschappelijke factor extraheren, impliceert dit dat een van de wortels van de polynoom

Alle wortels van de polynoom zijn dus als volgt:

In feite moet de polynoom zoveel wortels hebben als de graad aangeeft. In dit geval is de polynoom van graad 4 en heeft dus 4 wortels.

Factoring van polynomen met rationele wortels

Tot nu toe hebben we voorbeelden gezien van het ontbinden van polynomen met gehele wortels. Een polynoom kan echter ook rationale wortels hebben, dat wil zeggen met breuken. Laten we eens kijken hoe dit type polynoomfactorisaties wordt opgelost met een voorbeeld:

• Factor de volgende onvolledige polynoom:

Zoals altijd gebruiken we de regel van Ruffini met de delers van de onafhankelijke term om te proberen de wortels van de polynoom te bepalen:

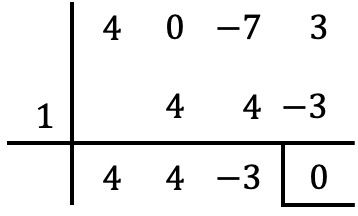
Maar we kunnen niet meer wortels berekenen met Ruffini, want als we Ruffini proberen te berekenen met alle andere delergetallen van de onafhankelijke term, krijgen we een andere rest dan nul.

We bevinden ons daarom in een situatie waar het alleen maar mee is

de rest van de deling is gelijk aan 0, dit betekent dat de polynoom breukwortels kan hebben. Om deze wortels te bepalen zouden we Ruffini met breuken kunnen toepassen, maar het is heel gemakkelijk om fouten te maken in de berekeningen en daarom doen we in deze gevallen meestal het volgende:

Als we de regel van Ruffini niet kunnen blijven toepassen met gehele wortels, moeten we de laatst verkregen polynoom gelijk stellen aan 0 en de resulterende vergelijking oplossen. De wortels van de polynoom zijn dus de waarden die uit de vergelijking worden gevonden.

Aan de andere kant, als de vergelijking geen oplossing heeft, betekent dit dat de polynoom geen wortels meer heeft en daarom niet volledig in factoren kan worden ontbonden.

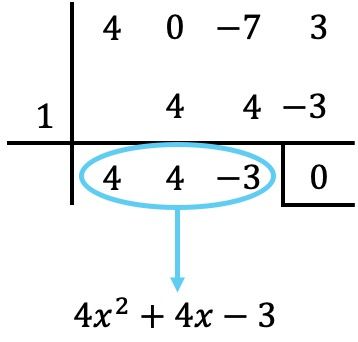
We stellen daarom het quotiëntpolynoom gelijk aan nul:

En we gebruiken de kwadratische vergelijkingsformule om de resulterende vergelijking op te lossen:

De wortels van de polynoom zijn daarom:

Het polynoom heeft dus wortels in de vorm van breuken.

En zodra we alle wortels van de polynoom kennen, kunnen we de in factoren verwerkte polynoom gemakkelijk vinden door elke wortel uit te drukken

in de vorm van een factor van het type

, dat wil zeggen dat je voor elke wortel een haakje met a moet plaatsen

en de wortel is van teken veranderd:

Houd er rekening mee dat u, om een polynoom in factoren te ontbinden, ook de factoren ervan moet vermenigvuldigen met de coëfficiënt van de term van de hoogste graad van het niet-gefactoriseerde polynoom, wat in dit geval 4 is.

Speciale gevallen van factoringpolynomen

Normaal gesproken wordt de regel van Ruffini (of synthetische deling) gebruikt om een polynoom in factoren te ontbinden, zoals hierboven uitgelegd. Maar afhankelijk van de polynoom van het probleem, kunt u soms sneller polynoomontbinden. We zullen elk van deze specifieke gevallen hieronder bekijken.

Belangrijke identiteiten in aanmerking nemen

Als we zien dat een polynoom overeenkomt met een opmerkelijke identiteit (of een opmerkelijk product), is het heel eenvoudig om deze in factoren te ontbinden. Om dit te kunnen doen moet je echter de formules voor opmerkelijke identiteiten beheersen, anders raad ik je aan om eens een kijkje te nemen op deze link waar je niet alleen de formules vindt, maar ook voorbeelden van notabelen kunt zien. identiteiten en je kunt zelfs oefeningen oefenen waarbij ze stap voor stap worden opgelost.

Verschil van vierkanten

Zoals u wel weet, is de formule voor de opmerkelijke identiteit van het verschil in vierkanten als volgt:

Daarom, als we een polynoom vinden die aan de uitdrukking voldoet

kan er direct rekening mee worden gehouden.

Kijk eens naar het volgende voorbeeld waarin rekening wordt gehouden met een verschil in vierkanten:

Aan de andere kant zijn de wortels van de polynoom:

Andere voorbeelden van het factoriseren van binominale waarden die verschillen in kwadraten zijn:

Optellen en aftrekken vierkant

Je zou de formules voor de twee belangrijkste resterende opmerkelijke identiteiten al moeten kennen: het optelvierkant en het aftrekkingsvierkant.

Dus als we ons realiseren dat een polynoom overeenkomt met een van deze twee opmerkelijke identiteiten, kunnen we deze direct ontbinden. Kijk naar de volgende voorbeelden:

Het identificeren van deze opmerkelijke productsoorten is iets moeilijker. Een truc is om te controleren of de onafhankelijke term van de polynoom het kwadraat is van een bepaald getal, en of de term van hogere graad het kwadraat is van een monomiaal (meestal

), in dit geval is het voldoende om te verifiëren dat het waar is

is gelijk aan het einde van het tussendiploma.

Als we bijvoorbeeld de volgende polynoom hebben:

In dit geval kan het alleen het kwadraat van een som zijn, omdat alle elementen van de polynoom positief zijn. De variabele dus

van de formule moet 5 zijn, omdat dit de wortel is van de onafhankelijke term en de variabele

het moet zijn

, aangezien het de wortel is van de term may degree.

Het enige wat we nu moeten doen is bewijzen dat de formule voor het kwadraat van de som vervuld is met de tussenliggende graadterm:

✅

Aan de formule voor het opmerkelijke product is voldaan, dus de meegerekende polynoom is:

En de wortel van deze polynoom is

dat is een dubbele wortel omdat de factor ervan kwadratisch is (deze wordt twee keer herhaald).

Hieronder staan meer voorbeelden van het factoriseren van perfecte vierkante trinomialen:

Het ontbinden van tweedegraads trinomialen

Zoals we zojuist hebben gezien, zijn er soms trinomialen die perfecte vierkanten zijn en deze kunnen direct worden verwerkt in de formules voor opmerkelijke identiteiten. Maar de meeste trinomialen zijn geen opmerkelijke producten, dus hoe bepalen we deze gevallen van polynomen?

Om een kwadratisch polynoom in factoren te ontbinden, is het niet nodig om de Ruffini-methode toe te passen; stel gewoon het polynoom gelijk aan nul en los de resulterende kwadratische vergelijking op. De oplossingen van de vergelijking zullen daarom de wortels van de polynoom zijn.

Als ons bijvoorbeeld wordt gevraagd de volgende polynoom van graad 2 te ontbinden:

In plaats van Ruffini te gebruiken, stellen we de polynoom gelijk aan 0:

En nu gebruiken we de formule van de tweedegraadsvergelijking om de oplossingen van de vergelijking te vinden:

De wortels van de polynoom zijn daarom:

En ten slotte is de polynomiale factorisatie:

Vierdegraads trinomialen ontbinden met even exponenten

Om een polynoom van de vierde graad met even exponenten te ontbinden, moeten we, net als in het vorige geval, het polynoom gelijk stellen aan nul en de bikwadraatvergelijking oplossen. Zodat de gevonden waarden overeenkomen met de wortels van de polynoom.

Als voorbeeld zullen we de volgende polynoom van graad 4 ontbinden:

Eerst stellen we de polynoom gelijk aan nul:

Nu moeten we de bikwadraatvergelijking oplossen. Om dit te doen, maken we een variabele wijziging:

We lossen de kwadratische vergelijking op met de formule:

We annuleren de verandering van de variabele om de wortels te berekenen:

De wortels van de polynoom zijn daarom:

En zodra we de wortels of nulpunten van de polynoom kennen, ontbinden we deze door de wortels algebraïsch uit te drukken in de vorm van factoren:

Polynomen in factoren ontbinden door te groeperen

In sommige zeer speciale gevallen kan een formule worden gebruikt om een heel specifiek type polynoom te ontbinden.

Als we een polynoom hebben met de volgende vorm:

We kunnen de polynoom vereenvoudigen door de gemeenschappelijke factor te verwijderen:

En de polynoom kan verder worden vereenvoudigd door de gemeenschappelijke factor een tweede keer te extraheren:

Op deze manier konden we de polynoom ontbinden in factoren zonder Ruffini of een andere methode toe te passen. En de wortels van genoemde polynoom zouden zijn:

Laten we nu deze methode bekijken met een numeriek voorbeeld:

Eerst verwijderen we de gemeenschappelijke factor met

en met 2:

En zoals nu

een gemeenschappelijke factor van de polynoom is, halen we de gemeenschappelijke factor eruit

De wortels van de polynoom zijn daarom:

Deze methode wordt ook wel factorisatie van polynomen genoemd door dubbele gemeenschappelijke factorextractie. Hoewel dit een zeer snelle procedure is, raden wij u af dit type factorisatie uit te voeren, omdat er vaak fouten worden gerapporteerd bij het factoriseren met deze methode. Bovendien kan, zoals we hierboven zagen, een polynoom van graad 2 ook in factoren worden verwerkt door een eenvoudige kwadratische vergelijking op te lossen. Kortom, er gebeurt niets als je deze methode niet goed begrijpt.

Ten slotte moet worden opgemerkt dat er nog andere, meer complexe polynomiale factorisatiemethoden bestaan, zoals het LLL-algoritme, de Kronecker-methode en de Trager-methode, die hier niet worden uitgelegd vanwege hun wiskundige moeilijkheid.

Opgeloste oefeningen over het ontbinden van veeltermen

Zodra u alle soorten factorpolynomen heeft gezien, raden wij u aan te oefenen met het oplossen van oefeningen. Daarom hebben we hieronder een aantal stapsgewijze opgeloste oefeningen voor het ontbinden van polynomen voorbereid. Houd er rekening mee dat als u vragen heeft, u deze in de opmerkingen kunt schrijven en dat wij ze snel zullen beantwoorden.

Oefening 1

Voer de factorisatie uit van de volgende polynoom van graad 3:

Het is een compleet, geordend, derdegraads en uiteindelijk onafhankelijk polynoom. Daarom passen we de methode van Ruffini toe om de wortels van de polynoom te bepalen:

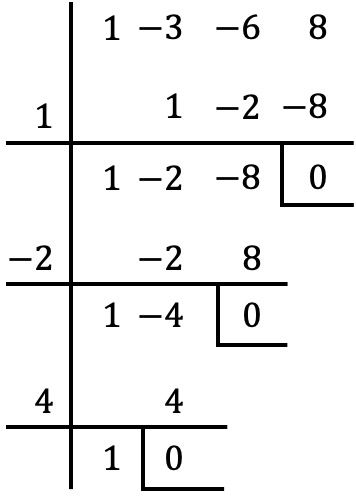
De wortels van de polynoom zijn daarom als volgt:

De polynomiale factorisatie is daarom:

Oefening 2

Bereken de factorisatie van de volgende polynoom van graad 4:

Het is een polynoom van de vierde graad en met een onafhankelijke term gebruiken we daarom de Ruffini-methode om de wortels van de polynoom te vinden:

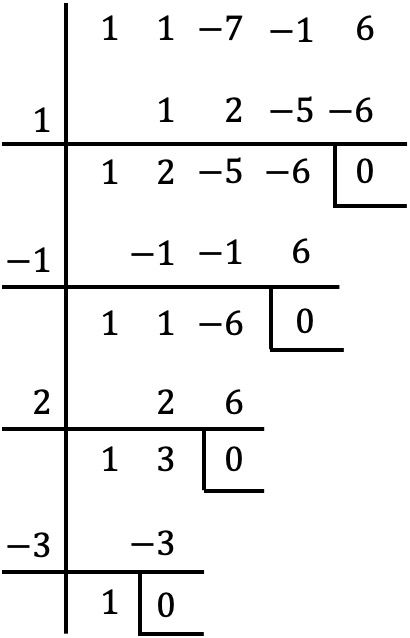
De wortels van de polynoom zijn daarom:

En als we de polynoom in factoren ontbinden, houden we over:

Oefening 3

Zoek de factorisatie van het volgende polynoom van de vierde graad:

In dit geval heeft de polynoom geen onafhankelijke term, we moeten eerst een gemeenschappelijke factor extraheren:

Nu we de gemeenschappelijke factor van x hebben genomen, berekenen we de wortels of nulpunten van de polynoom tussen haakjes met behulp van de methode van Ruffini:

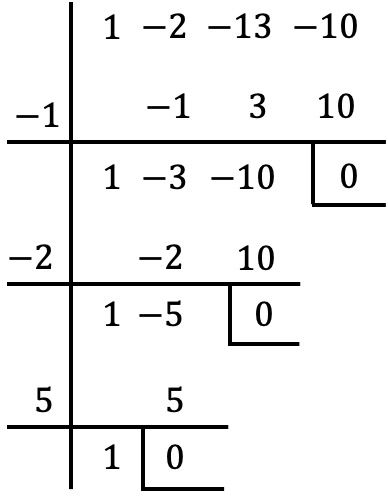
De wortels van de polynoom zijn dus de wortels die we hebben gevonden met de Ruffini-methode plus x=0 van de gemeenschappelijke factor:

En ten slotte verkrijgen we door de polynoom in factoren te ontbinden de volgende uitdrukking:

Oefening 4

Transformeer het volgende polynoom van de derde graad in factoren:

Deze polynoom heeft een onafhankelijke term, daarom berekenen we de wortels met het Ruffini-algoritme:

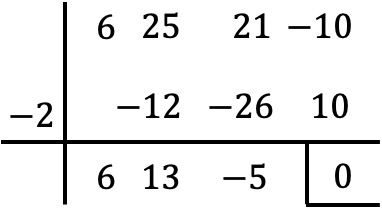
Wanneer we dit punt echter bereiken, kunnen we de regel van Ruffini niet blijven toepassen, omdat zonder nog een geheel getal de rest van de deling nul is.

Daarom stellen we de resulterende polynoom gelijk aan nul:

En we passen de formule van kwadratische vergelijkingen toe om de resulterende vergelijking op te lossen:

De wortels of nulpunten van de polynoom zijn daarom:

Dus de factorisatie van de polynoom moet gebeuren met breuken:

Oefening 5

Bepaal de factorisatie van het volgende polynoom van graad 6:

De polynoom in het probleem heeft geen onafhankelijke term, dus we moeten eerst de gemeenschappelijke factor extraheren, wat in dit geval het geval is

En zodra we de gemeenschappelijke factor uit de polynoom hebben verwijderd, vinden we de wortels van de polynoom tussen haakjes met behulp van de regel van Ruffini:

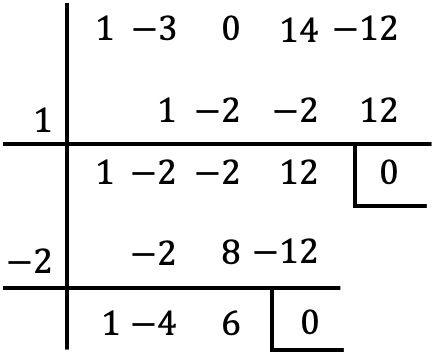
Maar als we dit stadium bereiken, kunnen we niet verder gaan, want zonder nog een geheel getal is de rest nul.

We stellen daarom de verkregen polynoom gelijk aan nul:

En we lossen de kwadratische vergelijking op met de formule:

Er zijn geen wortels van negatieve getallen, dus de vergelijking heeft geen oplossing, wat betekent dat we niet meer wortels van de polynoom kunnen vinden. Met andere woorden: de polynoom is niet volledig factoreerbaar.

De wortels die we hebben kunnen vinden zijn echter:

Merk op dat de wortel

wordt tweemaal herhaald omdat we de gemeenschappelijke factor hebben verwijderd

en aangezien het kwadraat is, impliceert dit dat het een dubbele wortel is.

Concluderend zal de in factoren verwerkte polynoom het product zijn van alle gevonden wortels, uitgedrukt als factoren

vermenigvuldigd met de polynoom verkregen uit de regel van Ruffini waarmee verder geen rekening kon worden gehouden:

Oefening 6

Voer de factorisaties uit van alle volgende polynomen:

De polynoom in sectie A) komt overeen met een opmerkelijke identiteit, met name het kwadraat van de som. De factorisatie is daarom:

De polynoom van sectie B) is ook een opmerkelijk product, met name het verschil tussen de vierkanten, dus:

Op dezelfde manier is de polynoom in sectie C) een opmerkelijke gelijkheid, in het bijzonder bestaat deze uit het kwadraat van een aftrekking. De factorisatie is daarom:

Ten slotte is de polynoom in deel D) geen opmerkelijke identiteit. We moeten daarom de polynoom gelijk stellen aan 0 en de resulterende vergelijking oplossen om de wortels ervan te vinden:

We gebruiken de kwadratische vergelijkingsformule:

De wortels van de polynoom D) zijn daarom:

En tenslotte is het resultaat van de polynomiale factorisatie: