Cette page explique comment multiplier un vecteur par un nombre réel (ou un scalaire) numériquement et graphiquement. De plus, vous trouverez également des exemples et des exercices résolus du produit d’un vecteur par un scalaire. Enfin, les propriétés de ce type d’opération avec des vecteurs sont également expliquées.
Comment multiplie-t-on un vecteur par un nombre réel ?
Pour calculer numériquement le produit d’un vecteur et d’un nombre (ou d’un scalaire), chaque composante du vecteur doit être multipliée par le nombre.
![]()
![]()
Ainsi, le résultat de la multiplication d’un vecteur par un nombre donne naissance à un nouveau vecteur avec les caractéristiques suivantes :
- Le résultat du produit d’un vecteur par un scalaire produit un nouveau vecteur de même direction que le vecteur d’origine.
- De plus, le nouveau vecteur aura la même direction si le nombre est positif.
- Ou il aura le sens opposé si le nombre est négatif.
- La magnitude du vecteur résultant est équivalente à la magnitude du vecteur d’origine multipliée par le scalaire.
Dans la représentation graphique suivante, vous pouvez voir comment la direction du vecteur est maintenue quel que soit le signe du scalaire. Par contre, le sens du vecteur dépend du signe du nombre qu’il multiplie.

De plus, dans le graphique suivant, on voit clairement que la magnitude du vecteur résultant du produit est égale à la magnitude du vecteur d’origine multiplié par le scalaire.
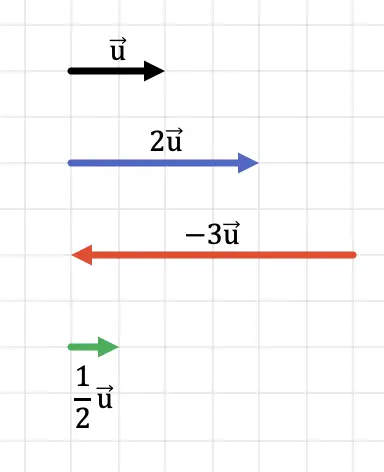
Évidemment, si nous multiplions le vecteur par un nombre supérieur à 1, le résultat est un vecteur de plus grande longueur (de plus grand module). D’autre part, si nous multiplions le vecteur par un nombre inférieur à 1, alors le résultat est un vecteur de longueur plus courte (module plus petit).
Remarque : Ne confondez pas le produit d’un vecteur et d’un scalaire avec le produit scalaire de vecteurs . Bien qu’ils aient un nom similaire, ce sont deux concepts totalement différents.
Exemple de produit d’un vecteur par un scalaire
Ensuite, nous allons voir un exemple numérique de la façon dont le produit d’un vecteur par un nombre est calculé :
- Multipliez le vecteur suivant par 4 :
![]()
![]()
Comme vous l’avez vu, ce type d’opération vectorielle n’est pas très compliqué, car vous n’avez pas à faire beaucoup de calculs.
Cependant, il existe des opérations vectorielles plus compliquées, telles que l’addition vectorielle et la soustraction vectorielle. Si vous avez déjà compris comment calculer le produit d’un vecteur et d’un scalaire, nous vous recommandons de passer au niveau suivant et de voir comment résoudre l’addition vectorielle et la soustraction vectorielle , car ce sont des opérations un peu plus difficiles et, en fait, elles sont beaucoup plus utilisées (elles sont plus importantes).
Propriétés de la multiplication d’un vecteur par un nombre
Le produit d’un vecteur et d’un nombre a les propriétés suivantes :
- Propriété associative : lorsque le vecteur est multiplié par plus d’un nombre, l’ordre des multiplications n’a pas d’importance.
![]()
- Propriété distributive par rapport à l’addition et à la soustraction de vecteurs :
![]()
![]()
- Propriété distributive par rapport à l’addition de scalaires :
![]()
- Élément neutre : Évidemment, tout vecteur multiplié par 1 donne le vecteur lui-même :
![]()
Problèmes résolus de multiplication d’un vecteur par un scalaire
Exercice 1
Calculez analytiquement le résultat du produit du vecteur suivant par 3 :
![]()
Pour trouver le produit il faut multiplier chaque coordonnée du vecteur par 3 :
![]()
Exercice 2
Multipliez le vecteur suivant par 6 et trouvez son module :
![]()
On fait d’abord la multiplication du vecteur par le scalaire :
![]()
Il existe maintenant deux façons de calculer la grandeur du vecteur obtenu. La première consiste à trouver la magnitude du vecteur d’origine, puis à la multiplier par 6 :
![]()
![]()
Et la deuxième façon est de calculer directement la grandeur du vecteur obtenu dans la multiplication :
![]()
De sorte qu’avec les deux procédures, il est démontré que le résultat ne dépend pas de la méthode par laquelle le module est calculé.
Exercice 3
Du vecteur suivant :
![]()
Calculez algébriquement les opérations suivantes :
![]()
![]()
![]()
![]()
Ensuite, déterminez si les vecteurs résultants ont la même direction et le même sens que le vecteur d’origine, et classez-les du plus court au plus long.
On calcule d’abord les multiplications :
![]()
![]()
![]()
![]()
Par conséquent, les vecteurs multipliés par des nombres positifs ont la même direction et la même direction que le vecteur d’origine. Et les vecteurs multipliés par des nombres négatifs ont la même direction mais la direction opposée au vecteur d’origine.
Vecteurs de même sens et de même sens :
![]() et
et![]()
Vecteurs avec la même direction mais une signification différente :
![]()
Enfin, il faut ordonner les vecteurs selon leur longueur, ou de manière équivalente, leur module. Le vecteur de longueur la plus longue (ou module le plus grand) sera celui qui aura été multiplié par un nombre plus grand (en valeur absolue), et le vecteur de longueur la plus courte (ou module le plus petit) sera celui qui aura été multiplié par un nombre plus petit (en valeur absolue). Donc l’ordre des longueurs est :
![]()
Notez que la longueur ou le module ne dépend pas du signe du scalaire qui s’est multiplié, puisque le sens du vecteur ne modifie pas son module.
Exercice 4
Soit les deux vecteurs suivants :
![]()
Calculez l’opération suivante :
![]()
On résout d’abord les multiplications de vecteurs par des nombres :
![]()
![]()
![]()
Et puis on soustrait les vecteurs :
![]()
![]()
Exercice 5
Effectuez les multiplications suivantes de vecteurs par des scalaires et représentez graphiquement les résultats :
![]()
![]()
![]()
![]()
![]()
On fait d’abord les multiplications des vecteurs par les scalaires réels :
![]()
![]()
![]()
![]()
![]()
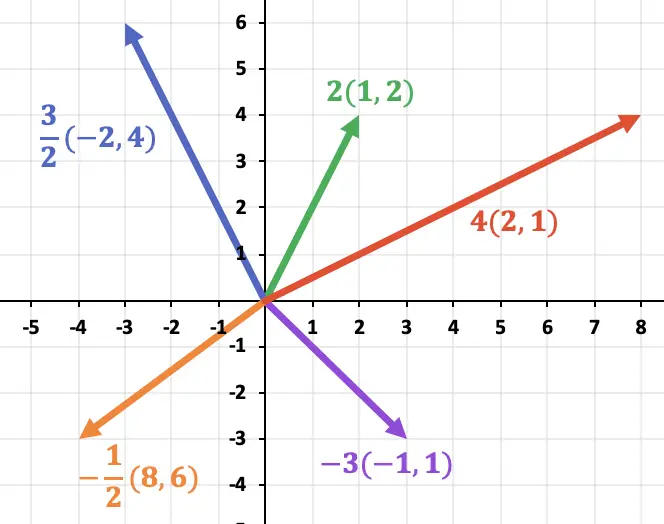
Enfin, une fois que nous avons calculé les vecteurs, nous les représentons dans le graphique :