Sur cette page nous allons voir comment multiplier un nombre par une matrice. Vous avez également des exemples qui vous aideront à le comprendre parfaitement et des exercices résolus pour que vous puissiez vous entraîner. Vous trouverez également toutes les propriétés du produit d’un scalaire et d’une matrice.
Comment faire une multiplication d’un nombre par une matrice ?
Pour multiplier un nombre par une matrice , multipliez chaque élément de la matrice par le nombre.
Exemple:

Problèmes résolus de multiplication d’un nombre par une matrice
Exercice 1 :
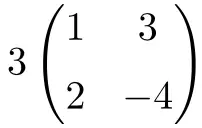
C’est une multiplication d’un scalaire par une matrice carrée d’ordre 2 :
![Rendered by QuickLaTeX.com \displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-590b79c0fea524b963397181b6f2bea8_l3.png)
Exercice 2 :
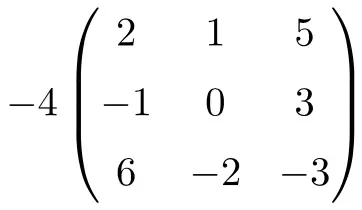
C’est un produit d’un nombre par une matrice carrée d’ordre 3 :
![Rendered by QuickLaTeX.com \displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5042f0f8cd9b7a4d0e28974f793b145b_l3.png)
Exercice 3 :
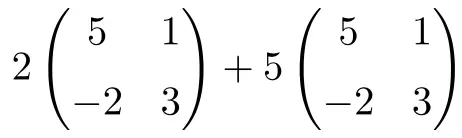
C’est une opération qui combine des produits de nombres par des matrices et des sommes de matrices de dimension 2×2 :
![Rendered by QuickLaTeX.com \displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56d2a40f021be13a5d92d0c10d353684_l3.png)
Par conséquent, nous devons d’abord résoudre pour les produits:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-068901abef987767025bb01b24579226_l3.png)
Et enfin on fait la somme des matrices résultantes :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d15ea16036f522af0f23fee0bb796757_l3.png)
Exercice 4 :
Soit les matrices suivantes :
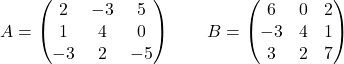
Calculer:
![]()
C’est une opération qui combine des multiplications scalaires avec des additions et des soustractions de matrices de dimension 3×3. De plus, la matrice
![]() est la matrice identité, qui est composée de 1 sur la diagonale principale et de 0 sur le reste des éléments :
est la matrice identité, qui est composée de 1 sur la diagonale principale et de 0 sur le reste des éléments :
![Rendered by QuickLaTeX.com \displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dce934040dc05714321dbbeac4e20c73_l3.png)
Par conséquent, nous effectuons d’abord les multiplications :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc26f29384abcfb6f08a36b601e4ff61_l3.png)
On additionne les deux premières matrices :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-897ec02d46bc09bdec58d9b3246c6f4d_l3.png)
Enfin, on effectue la soustraction des matrices :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ddd808a46a137f4c7742545c4f76f46_l3.png)
Si ces exercices sur les produits scalaires matriciels vous ont été utiles, n’hésitez pas à vous exercer avec les exercices résolus pas à pas sur l’ addition de matrices et le produit de matrices , les deux types d’opérations matricielles qui se répètent le plus.
Propriétés du produit d’un nombre par une matrice
Comme vous le savez bien, il existe de nombreux types de matrices : les matrices carrées, les matrices triangulaires, la matrice identité,… Mais, heureusement, toutes les propriétés du produit de nombres par des matrices sont valables pour toutes les classes de matrices.
Voici donc les propriétés de la multiplication entre scalaires et matrices :
- Propriété associative :
![]()
Regardez les deux opérations suivantes car elles donnent le même résultat, quelle que soit la façon dont nous multiplions le 2 et le 3 :
![Rendered by QuickLaTeX.com \displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4e9fd568edd5833238d8d21fdf4d1a8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f8ee596b3e2ca16ff1c507717982ee1_l3.png)
- Propriété distributive par rapport à l’addition de scalaires :
![]()
Comme vous pouvez le voir dans l’exemple ci-dessous, il en va de même si nous additionnons d’abord 1+2 puis le multiplions par une matrice, ou si nous multiplions la matrice séparément par 1 et par 2 puis additionnons les résultats :
![Rendered by QuickLaTeX.com \displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-025ac9b0851ed93fd0c3870328d6144b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f54f4d5ae113e2462b752c150b3f43b_l3.png)
- Propriété distributive par rapport à l’addition de matrices :
![]()
Autrement dit, ajouter deux matrices mathématiques puis les multiplier par un nombre équivaut à multiplier séparément les deux matrices par le même nombre puis à additionner les résultats. Dans l’exemple ci-dessous, vous pouvez vérifier :
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdb35d5c66ee525c3d52fe7576e75758_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ef9d3f8f503371fa5f3d2478f728d88_l3.png)
- Propriété de l’élément neutre :
![]()
Par conséquent, en multipliant une matrice par 1, nous ne modifions pas la matrice :
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ee2c0afd1bf2904722701caca883125_l3.png)
Ce sont toutes les propriétés du produit d’un scalaire et d’une matrice, c’est donc la fin de cet article. Nous espérons que cela vous a plu et, surtout, que vous avez appris à résoudre la multiplication de nombres avec des matrices.
Par contre, d’autres opérations matricielles liées à la multiplication, et qui sont très utiles, sont les puissances. Ici, nous vous laissons la page où vous apprendrez ce que c’est et comment résoudre la puissance d’une matrice , au cas où vous seriez curieux.