Dans cet article, nous expliquons comment connaître la monotonie d’une fonction, c’est-à-dire comment trouver les intervalles d’augmentation et de diminution d’une fonction. De plus, vous pouvez vous entraîner avec des exercices étape par étape sur la croissance et le déclin d’une fonction.
Qu’est-ce que la monotonie d’une fonction ?
Une fonction est monotone sur un intervalle si elle conserve l’ordre donné. Il existe cinq types de monotonie :
- Fonction monotone croissante : lorsque la valeur de la fonction en un point est toujours égale ou supérieure à la valeur de la fonction en un point précédent.
- Fonction croissante strictement monotone : lorsque la valeur de la fonction en un point est toujours supérieure à la valeur de la fonction en un point précédent.
- Fonction constante lorsque la valeur de la fonction en un point est toujours égale à la valeur de la fonction en un point précédent.
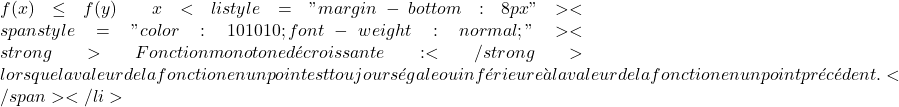f(x)\geq f(y) \qquad x
f(x)>f(y) \qquad x
f(x)=\cfrac{3}{x^2-4}
x^2-4=0x^2=4x=\pm 2
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left(x^2-4\right)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
\left(x^2-4\right)^2}
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
f'(x)=0,
f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}f'(-3) = \cfrac{-6\cdot(-3)}{\left((-3)^2-4\right)^2} = \cfrac{+18}{+25} = +0,72 \ \rightarrow \ \bm{+}f'(-1) = \cfrac{-6\cdot(-1)}{\left((-1)^2-4\right)^2} = \cfrac{+6}{+9} = +0,67 \ \rightarrow \ \bm{+}f'(1) = \cfrac{-6\cdot 1}{\left(1^2-4\right)^2} = \cfrac{-6}{+9} = -0,67 \ \rightarrow \ \bm{-}f'(3) = \cfrac{-6\cdot3}{\left(3^2-4\right)^2} = \cfrac{-18}{+25} = – 0,72 \ \rightarrow \ \bm{-}
\bm{(-\infty, -2)\cup (-2,0)}
\bm{(0,2)\cup (2,+\infty)}
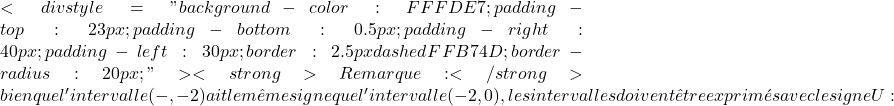(-\infty, -2)\cup (-2,0)
(-\infty,0)
\displaystyle f(x)=x^3-6x^2+9x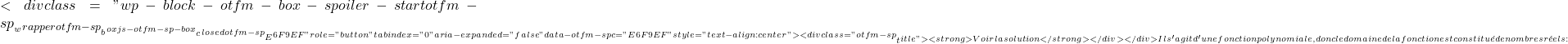 
\text{Dom } f= \mathbb{R} 
f'(x)=0.
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
f'(x)= 03x^2-12x+9=0\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(-12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108}}{6} =\cfrac{12 \pm 6}{6}=\begin{cases} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6}=1 \end{cases} \end{aligned}
f'(x)=0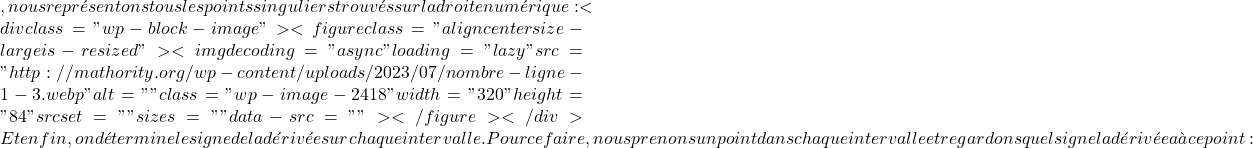
f'(0)=3\cdot 0^2-12\cdot0+9 =+9 \ \rightarrow \ \bm{+}f'(2)=3\cdot2^2-12\cdot2+9 =-3 \ \rightarrow \ \bm{-}f'(4)=3\cdot4^2-12\cdot4+9 =+9 \ \rightarrow \ \bm{+}
\bm{(-\infty, 1)\cup (3,+\infty)}\bm{(1,3)}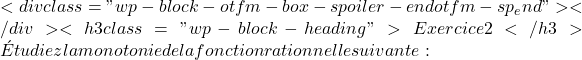
\displaystyle f(x)=\frac{5}{x^2-9} 
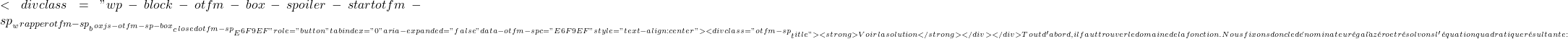x^2-9 = 0 x^2 = 9 x = \pm 3 
\text{Dom } f= \mathbb{R}-\{+3, -3 \} 
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\left(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 -10x= 0 x= \cfrac{0}{-10} x=0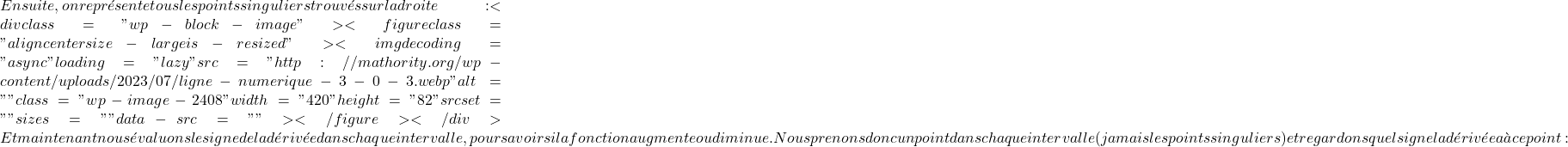 
f'(-4)= \cfrac{-10(-4)}{\left((-4)^2-9\right)^2}= \cfrac{+40}{+49} =+0,82 \ \rightarrow \ \bm{+}f'(-1)= \cfrac{-10(-1)}{\left((-1)^2-9\right)^2}= \cfrac{+10}{+64} = +0,16 \ \rightarrow \ \bm{+}f'(1)= \cfrac{-10\cdot 1}{\left(1^2-9\right)^2}= \cfrac{-10}{+64} = -0,16 \ \rightarrow \ \bm{-}f'(4)= \cfrac{-10\cdot 4}{\left(4^2-9\right)^2}= \cfrac{-40}{+7} =-0,82 \ \rightarrow \ \bm{-}
\bm{(-\infty, -3)\cup (-3,0)}\bm{(0,3)\cup (3,+\infty)}
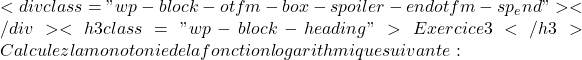\displaystyle f(x)=\ln\left(x^2+1\right) 
x^2+1> 0
\text{Dom } f= \mathbb{R} 
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x)= \cfrac{2x}{x^2+1}f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} x=0 
f'(-1)= \cfrac{2\cdot(-1)}{(-1)^2+1}= \cfrac{-2}{+2} = -1 \ \rightarrow \ \bm{-}f'(1)= \cfrac{2\cdot1}{1^2+1}= \cfrac{+2}{+2} = +1 \ \rightarrow \ \bm{+}
\bm{(0,+\infty)}\bm{(-\infty,0)}$