Comment calculer le module d'un vecteur

Sur cette page, vous verrez l’explication de la magnitude d’un vecteur et comment la calculer avec sa formule. Vous pourrez également voir comment trouver le module à partir de deux points : son origine et sa fin. De plus, vous découvrirez comment déterminer les composantes d’un vecteur à partir de son module et les propriétés du module d’un vecteur. Vous pouvez même vous entraîner avec des exemples, des exercices et des problèmes résolus étape par étape.

Qu’est-ce que le module d’un vecteur ?

La magnitude d’un vecteur représente la distance entre son origine et sa fin. Par conséquent, la grandeur d’un vecteur est égale à la longueur dudit vecteur.

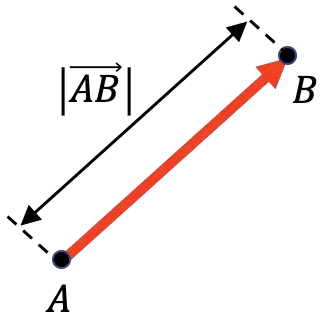
Comme vous pouvez le voir dans la représentation graphique ci-dessus, la magnitude d’un vecteur est symbolisée par une barre verticale de chaque côté du vecteur :

$\lvert \vv{AB}\rvert$

D’autre part, le module d’un vecteur est le même que la norme d’un vecteur , vous pouvez donc le voir également écrit de cette façon. C’est pourquoi il y a des mathématiciens qui représentent aussi le module d’un vecteur avec deux barres verticales de chaque côté :

$\lvert \lvert \vv{AB}\rvert\rvert$

Formule du module d’un vecteur

Pour trouver la magnitude d’un vecteur dans le plan, il faut appliquer la formule suivante :

Pour déterminer la grandeur d’un vecteur, nous devons calculer la racine carrée (positive) de la somme des carrés de ses composantes. Autrement dit, si nous avons le vecteur suivant :

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Son module est :

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Par exemple, nous allons calculer la magnitude du vecteur suivant à l’aide de la formule :

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Calculer la magnitude d’un vecteur avec les coordonnées de son origine et de sa fin

Nous venons de voir comment la grandeur d’un vecteur est déterminée lorsque nous connaissons ses composantes, mais que se passerait-il si nous ne connaissions que les points où il commence et où il se termine ?

Ainsi, pour calculer la magnitude d’un vecteur à partir des coordonnées de son origine et de sa fin, il faut suivre ces deux étapes :

On trouve d’abord les composantes du vecteur. Pour ce faire, nous devons soustraire l’extremum moins l’origine.
Et puis on calcule le module du vecteur obtenu avec la formule que l’on a vu dans la section précédente.

Voyons comment cela se fait à travers un exemple :

Calculer la grandeur du vecteur dont l’origine est le point 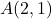$A(2,1)$ et comme point final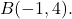 $B(-1,4).$

Nous devons d’abord trouver les composantes du vecteur, nous soustrayons donc son extrémité moins son origine :

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Une fois que nous connaissons le vecteur, nous calculons sa magnitude en utilisant la formule de la magnitude d’un vecteur :

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

Et nous laissons le résultat sous la forme d’une racine carrée, car il n’est pas exact.

Comment calculer les composantes d’un vecteur à partir de son module

Nous avons vu comment extraire la magnitude d’un vecteur de ses composants, mais le processus peut aussi être inversé. Autrement dit, nous pouvons calculer les composantes d’un vecteur à travers son module.

Le processus qui permet de trouver les composantes d’un vecteur à partir de sa grandeur est appelé décomposition vectorielle . Ainsi, pour décomposer un vecteur, nous avons besoin de sa grandeur, évidemment, et de l’angle qu’il forme avec l’axe des abscisses (axe X).

Pour que les composantes X et Y du vecteur puissent être calculées avec les rapports trigonométriques :

Comme vous pouvez le voir sur l’image, la magnitude d’un vecteur forme un triangle rectangle avec ses composants, de sorte que les formules élémentaires de la trigonométrie peuvent être appliquées.

Il faut tenir compte du fait que, contrairement au module d’un vecteur, ses composantes peuvent être négatives car le sinus et le cosinus peuvent prendre des valeurs négatives.

A titre d’exemple, nous allons résoudre la décomposition vectorielle du vecteur dont la grandeur et l’angle avec l’axe OX sont :

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

La composante horizontale du vecteur est égale au module multiplié par le cosinus de l’angle :

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

Et la composante verticale du vecteur est égale à la multiplication du module par le sinus de l’angle :

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

Donc le vecteur est le suivant :

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Propriétés du module d’un vecteur

Le module est un type d’opération vectorielle qui présente les caractéristiques suivantes :

La magnitude d’un vecteur ne peut jamais être négative , elle sera toujours égale ou supérieure à 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

En fait, le seul vecteur qui existe avec une magnitude nulle est le vecteur nul, c’est-à-dire le vecteur

$\vv{\text{u}}= (0,0) .$

La grandeur du produit d’un vecteur par un nombre réel (ou un scalaire) équivaut à multiplier la valeur absolue du scalaire par la grandeur du vecteur. Par conséquent, l’égalité suivante est vérifiée :

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

L’ inégalité triangulaire est vérifiée : le module de la somme de deux vecteurs est inférieur ou égal à la somme de leurs modules séparément.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

De plus, l’amplitude de la somme de deux vecteurs est liée au produit scalaire par l’équation suivante :

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

vecteur unitaire

En mathématiques, un vecteur unitaire est un vecteur dont le module est égal à un.

$\lvert \vv{\text{u}} \rvert=1$

Par conséquent, la longueur d’un vecteur unitaire est une unité.

Il peut sembler très difficile pour un vecteur d’avoir un module d’exactement 1, mais il est en fait facile de trouver ce type de vecteur :

Pour trouver le vecteur unitaire de n’importe quel vecteur, il suffit de le diviser par son module :

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Où

$\vv{\text{v}}_u$ est le vecteur unitaire de $\vv{\text{v}},$ et $\lvert \vv{\text{v}} \rvert$ votre module.

Le vecteur unitaire est également appelé verseur ou vecteur normalisé.

De plus, le vecteur unitaire a la même direction et la même direction que le vecteur d’origine.

Par exemple, nous allons calculer le vecteur unitaire du vecteur suivant :

$\vv{\text{v}}=(1,-1)$

Pour normaliser le vecteur, nous devons d’abord calculer sa magnitude :

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

Et, enfin, nous calculons le vecteur unitaire en divisant le vecteur original par son module :

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Exercices résolus de modules de vecteurs

Exercice 1

Calculez la magnitude du vecteur suivant :

$\vv{a}=(6,8)$

voir solution

Pour calculer le module du vecteur nous devons appliquer sa formule :

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Exercice 2

Ordonnez les vecteurs suivants du plus court au plus long.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

voir solution

La longueur d’un vecteur est égale à sa grandeur. Par conséquent, nous devons calculer les modules de tous les vecteurs :

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

Ainsi, les vecteurs ordonnés de la plus petite à la plus grande longueur (ou module) sont :

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Exercice 3

Détermine la grandeur du vecteur dont l’origine est le point

$A(-3,2)$ et comme point final $B(7,-4).$

voir solution

Pour calculer son module, il faut d’abord trouver le vecteur. Pour ce faire, on soustrait l’extremum moins l’origine :

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Une fois que nous connaissons le vecteur, son module est calculé à l’aide de la formule du module :

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Exercice 4

Décomposez le vecteur suivant et trouvez ses composants :

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

voir solution

La composante horizontale du vecteur est égale au module multiplié par le cosinus de l’angle :

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

Et la composante verticale du vecteur est égale à la multiplication du module par le sinus de l’angle :

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

Donc le vecteur est le suivant :

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

Dans ce cas, les deux composantes sont identiques, c’est-à-dire que l’angle d’inclinaison du vecteur est de 45º.

Exercice 5

Calculez le vecteur de même direction et de même direction que le vecteur suivant mais avec le module 1.

$\vv{a} = (-4,3)$

voir solution

Le vecteur de même direction et de même sens mais de module 1 est le vecteur unitaire. Pour le calculer, on trouve d’abord le module du vecteur :

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

Et maintenant nous calculons le vecteur unitaire en divisant le vecteur original par son module :

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

Exercice 6

Décomposez vectoriellement le vecteur suivant et calculez son vecteur unitaire :

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

voir solution

Tout d’abord, nous décomposons le vecteur et trouvons ses coordonnées :

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

Donc le vecteur est le suivant :

$\vv{a}= (5,64 \ ,\ 2,05)}$

Et maintenant on calcule le vecteur unitaire en divisant le vecteur obtenu par son module :

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

Notez que les composantes d’un vecteur unitaire sont égales au cosinus et au sinus de l’angle qu’il forme avec l’axe X.

Comment calculer le module d’un vecteur

Qu’est-ce que le module d’un vecteur ?

Formule du module d’un vecteur

Calculer la magnitude d’un vecteur avec les coordonnées de son origine et de sa fin

Comment calculer les composantes d’un vecteur à partir de son module

Propriétés du module d’un vecteur

vecteur unitaire

Exercices résolus de modules de vecteurs

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Leave a Comment Cancel Reply