La méthode des moindres carrés est un outil mathématique permettant de trouver la meilleure ligne droite correspondant à un ensemble de points . Nous vous l’expliquons de manière simple :
Imaginez que vous ayez un ensemble de points sur un graphique éparpillés ici et là. Vous voulez trouver une ligne droite qui « correspond » le mieux à ces points, de manière à minimiser la distance entre la ligne et les points . C’est l’idée derrière la méthode des moindres carrés.
La méthode utilise une formule pour calculer l’équation de la droite qui minimise la somme des carrés des différences entre les points et la droite. C’est-à-dire qu’il recherche la ligne qui a la plus petite “déviation” par rapport aux points.
En termes simples, la méthode des moindres carrés est utile pour l’analyse des données obtenues lors d’une enquête, dans le but d’exprimer leur comportement de manière linéaire, en réduisant les erreurs des informations volées.
Qui a créé la méthode des moindres carrés ?
La méthode des moindres carrés, outil fondamental dans les statistiques et l’analyse des données, est attribuée au mathématicien allemand Carl Friedrich Gauss , qui l’a proposée en 1794. Cependant, Gauss ne l’a publiée qu’en 1809 .
Fait intéressant, le mathématicien français Andrien-Marie Legendre a publié une version similaire en 1805 , en la développant indépendamment.
Les deux mathématiciens ont contribué à la création de cette méthode qui a été largement utilisée dans diverses disciplines pour ajuster les modèles aux données observées et faire des prédictions précises.
Formule de la méthode des moindres carrés
Sans doute, pour comprendre ce qu’implique cette méthode, il est indispensable d’en expliquer la formule et le processus de réalisation. Voici une explication détaillée de la formule de la méthode des moindres carrés :
définir le problème
Supposons que vous ayez un ensemble de données avec deux variables, une variable indépendante (x) et une variable dépendante (y), et que vous souhaitiez ajuster une ligne droite à ces données.
L’objectif est de trouver les valeurs des coefficients de l’équation de la droite (ordonnée à l’origine et pente) qui minimisent la somme des carrés des différences entre les valeurs réelles de y, et les valeurs prédites par la droite ajustée.
Calculer l’équation de la droite
L’équation d’une droite a la forme y = mx + b, où m est la pente et b est l’ordonnée à l’origine. La formule de la méthode des moindres carrés pour calculer les valeurs de myb est la suivante :
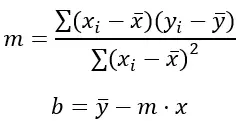
Où:
Σ représente la somme des valeurs.
x i et y i sont les valeurs des variables x et y respectivement pour chaque point de données.
x̄ et ȳ sont les moyennes des valeurs de x et y respectivement.
(x i – x̄) et (y i – ȳ) sont les différences entre les valeurs de x et y et leurs moyennes respectives.
(x i – x̄) 2 est le carré de la différence entre la valeur de x et sa moyenne.
interpréter les résultats
Une fois que vous avez calculé les valeurs de m et b à l’aide de la formule, vous pouvez les utiliser pour obtenir l’équation de la droite ajustée. Par exemple, si vous avez m = 2 et b = 3, alors l’équation de la droite ajustée serait y = 2x + 3. Cela vous permet de faire des prédictions ou des estimations des valeurs y pour différentes valeurs de x en fonction de la droite ajustée.
Dans quels cas la méthode des moindres carrés est-elle utilisée ?
Vous vous demanderez sûrement quand cette méthode est-elle utilisée ? Il est très utile dans diverses situations! Par exemple, lorsque vous souhaitez analyser des données expérimentales ou de recherche pour trouver une relation ou une tendance .
Supposons que vous enquêtiez sur la relation entre le prix d’une maison et sa taille en mètres carrés. Vous pouvez utiliser la méthode des moindres carrés pour trouver la ligne droite qui correspond le mieux aux données et vous donne une idée claire de cette relation.
Il est également utilisé en économie pour modéliser et prédire des variables telles que la demande de produits ou le comportement des prix . De plus, en ingénierie, la méthode des moindres carrés est appliquée pour ajuster les modèles mathématiques aux données de test ou de simulation.
La méthode des moindres carrés est un outil puissant et polyvalent qui est utilisé dans de nombreux domaines d’étude et de travail pour analyser des données et trouver des relations importantes.
Applications de la méthode des moindres carrés dans d’autres théorèmes
En plus de son utilisation en elle-même, la méthode des moindres carrés est très utile dans d’autres théorèmes. Voyons un peu plus sur le sujet, ci-dessous.
Théorème de régression
Il est largement utilisé dans le théorème de régression pour trouver la meilleure ligne qui correspond à un ensemble de données . Par exemple, vous pouvez l’utiliser pour analyser la relation entre la hauteur d’une plante et la quantité de lumière qu’elle reçoit pour déterminer comment la plante poussera dans différentes conditions d’éclairage.
Théorème d’interpolation
Dans ce cas, la méthode des moindres carrés est également appliquée dans le théorème d’interpolation pour trouver la fonction polynomiale qui correspond le mieux à un ensemble de points. Par exemple, vous pouvez l’utiliser pour approximer la trajectoire d’un objet en mouvement en fonction des données de position et de temps.
Théorème d’ajustement de courbe
Il est utilisé dans le théorème d’ajustement de courbe pour trouver une courbe qui correspond à un ensemble de données . Ceci est utile dans des applications telles que la modélisation des données climatiques pour prédire le changement climatique ou pour prédire la trajectoire d’un projectile.
Théorème d’analyse de Fourier
Dans le théorème d’analyse de Fourier, la méthode des moindres carrés est utilisée pour approximer une fonction périodique à partir d’une série de données discrètes . Cela s’applique à la signalisation des données et à la compression des images et du son.
Théorème de régression non linéaire
Enfin, la méthode des moindres carrés est également appliquée dans le théorème de régression non linéaire pour trouver la meilleure courbe qui correspond à un ensemble de données qui ne suit pas une relation linéaire . Par exemple, vous pouvez l’utiliser pour analyser comment la concentration d’un produit chimique affecte la vitesse de réaction.
Exemple de la méthode des moindres carrés
Pour mieux comprendre comment vous pouvez appliquer la méthode des moindres carrés, regardons un exemple ci-dessous.
Supposons que vous disposiez des données de hauteur suivantes (en centimètres) d’une plante au cours de différentes semaines :
| Semaine | hauteur en centimètres |
| 1 | dix |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | vingt |
Vous voulez trouver la meilleure ligne droite adaptée à ces données pour faire une prédiction de la hauteur future de la plante.
Étape 1 : Représenter graphiquement les données
La première chose à faire est de tracer les données sur un nuage de points. L’axe des x représentera les semaines et l’axe des y représentera la taille en centimètres. Voici le graphique :
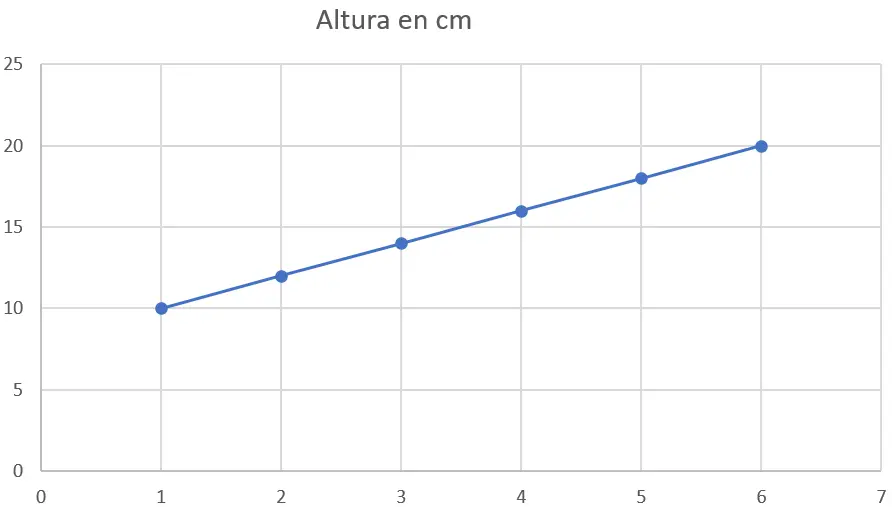
Etape 2 : Appliquer la méthode des moindres carrés
La méthode des moindres carrés cherche à trouver une droite qui minimise la somme des carrés des différences entre les données réelles et les valeurs prédites par la droite. Dans ce cas, la ligne est représentée par l’équation d’une ligne : y = mx + b, où “y” est la hauteur, “x” est les semaines, “m” est la pente de la ligne et “b” est l’ordonnée à l’origine.
Pour trouver les valeurs de “m” et “b” qui minimisent la somme des carrés des différences, les formules suivantes sont utilisées :
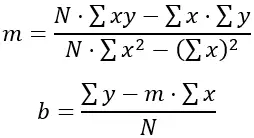
Où N est le nombre de points de données (dans ce cas, 6), Σxy est la somme des semaines multipliée par les hauteurs, Σx est la somme des semaines, Σy est la somme des hauteurs et Σx 2 est la somme des carrés des semaines.
En appliquant ces formules aux données de hauteur, nous obtenons :
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
En substituant ces valeurs dans les formules pour “m” et “b”:
m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2,07
b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24
Par conséquent, l’équation de la ligne droite qui correspond aux données de hauteur est : y.