Sur cette page, vous verrez ce qu’est la matrice Identité (ou Unité) ainsi que plusieurs exemples. De plus, nous expliquons quelles sont les propriétés de la matrice d’identité, comment fonctionner avec ce type de matrice et quel est le résultat de son déterminant. Enfin, vous trouverez les applications que possède cette matrice très particulière.
Qu’est-ce que la matrice d’identité ?
La matrice Identité (ou Unité) est une matrice carrée remplie de zéros (0) sauf sur la diagonale principale, où tous les éléments sont des uns (1).
C’est la définition de la matrice d’identité ou de la matrice d’unité, mais vous la verrez sûrement plus clairement à travers des exemples :
Exemples de matrices d’identités
Exemple de matrice d’identité de dimension 2 × 2
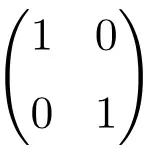
Exemple de matrice Identité d’ordre 3×3

Exemple de matrice Identité de taille 4×4
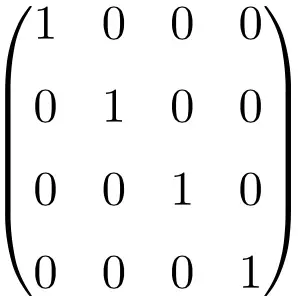
Comme vous pouvez le voir, pour construire la matrice d’identité, nous devons toujours suivre la même procédure : mettre des uns (1) sur la diagonale principale et le reste tous des zéros (0). La seule chose qui change est la dimension du tableau.
Propriétés du tableau d’identité
La matrice d’identité, la matrice d’unité ou même la matrice identique est largement utilisée en mathématiques, et cela est dû aux caractéristiques que possède ce type de matrice :
- La matrice d’identité est un exemple de matrice diagonale .
- Une matrice unitaire est à la fois une matrice triangulaire supérieure et inférieure.
- La matrice d’identité est également une matrice symétrique .
- L’ adjoint de la matrice d’identité est lui-même.
![Rendered by QuickLaTeX.com \displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16454b80729e9e2059e118dfc5ba2f8a_l3.png)
- C’est une matrice inversible. Et, comme pour l’adjoint, l’ inverse de la matrice Unité est lui-même :
![Rendered by QuickLaTeX.com \displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e9ca14cfbc1b230347abb6e36464e9c_l3.png)
- Toute matrice scalaire peut être obtenue à partir de la multiplication d’un nombre par la matrice d’identité :
![Rendered by QuickLaTeX.com \displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ba48a8806ab085937939bada831e91e_l3.png)
- Toutes les valeurs propres (ou valeurs propres) de la matrice Identique sont 1 :
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b9a461140ed125bbcc26d551b255cdc_l3.png)
- Enfin, la matrice d’identité est également un exemple de matrice de permutation .
Opérations avec la matrice Identité (ou Unité)
Vous pensez sûrement : tout cela est très bien mais… et à quoi sert la matrice d’Identité ? Si seulement c’était un tableau avec des 0 et des 1 !
Bien que vous n’ayez peut-être pas encore donné ce sujet, la matrice d’identité est beaucoup utilisée en mathématiques, en fait, ce type de matrice carrée est très important en algèbre linéaire. La principale utilité de la matrice d’identité est la facilité avec laquelle elle permet les calculs d’opérations matricielles. Voyons donc comment fonctionner avec la matrice Identity :
Additionner et soustraire avec la matrice Identity
Une façon d’ajouter (ou de soustraire) des nombres sur la diagonale principale d’une matrice sans modifier les autres éléments consiste à utiliser la matrice d’identité, car elle n’ajoute (ou ne soustrait) qu’une unité à ces éléments :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a357b8c79a1f4f70a5dcdeadcbe3e46_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f549edd3cac0340615dae86bf7e2932_l3.png)
Vous pouvez également ajouter ou soustraire plus d’unités aux éléments sur la diagonale en multipliant d’abord la matrice d’identité par un scalaire :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-85520cb04e8697d315a6e5002c8e1dea_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a90c8c3b8f9635561f6c85e7b003734c_l3.png)
Multiplication d’une matrice par la matrice identité
Lors de la multiplication d’une matrice par la matrice d’identité, elle agit comme un élément neutre , c’est-à-dire que toute matrice multipliée par la matrice d’identité donne la même matrice. Jetez un œil à l’exemple suivant :
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-345f47fb447c1877462d8c9358f8eb89_l3.png)
De plus, la signification du produit matriciel est indifférente, ou en d’autres termes, peu importe si nous multiplions la matrice d’identité par la droite ou par la gauche car le résultat sera toujours la même matrice. Pour le démontrer, nous répétons l’exercice précédent mais cette fois en multipliant la matrice d’Identité par le côté opposé :
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9a6c50074dc2594054453a6b53f4862_l3.png)
Puissance de la matrice identité
La puissance de la matrice d’identité se traduit toujours par la matrice d’identité, quel que soit l’exposant auquel nous élevons la matrice et la dimension de la matrice.
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e8dbc082f20a9a9b5b5c9b1b443833c4_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67a36555e36ab97ce2c663bf32c8e97d_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2efa9dcf6ec3b986aaff19701a794899_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14cad3370ec38fd0ed7ebb3a5fa96282_l3.png)
Déterminant de la matrice identité
Comme je suppose que vous l’imaginez déjà, le déterminant de la matrice Identité (ou Unité) est toujours égal à 1 , quelle que soit la dimension de la matrice.
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-718871901f1660f8f5202ea312c39584_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5971cf3c43e11184380d55d43f69ba8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4efd00fdafcbe456d1b5060344fe8d5_l3.png)
Applications de matrice d’identité
Enfin, après toutes ces informations, vous savez sûrement déjà comment répondre à la question typique de savoir pourquoi la matrice d’identité est-elle si importante ? Détendez-vous, je me suis aussi posé cette question avant. 😂
Comme vous l’aurez constaté, la matrice d’identité a de nombreuses utilisations et c’est pourquoi elle est si intéressante. L’une des utilisations de la matrice Unit est les opérations, car, comme nous l’avons vu, il est très facile d’effectuer des opérations matricielles avec elle.
D’autre part, la matrice d’identité est également utilisée pour résoudre des équations matricielles . Pour ce faire, on utilise la propriété de matrice inverse suivante : la multiplication d’une matrice par sa matrice inversée est égale à la matrice d’identité. Vous pouvez voir comment résoudre une équation avec des matrices en cliquant sur le lien.
De plus, la matrice d’identité est également utilisée pour calculer la matrice inverse avec la méthode gaussienne. Cette méthode consiste à placer une matrice à côté de la matrice d’identité, formant ainsi une matrice plus grande. Ensuite, la matrice d’origine doit être transformée en matrice d’identité en appliquant des opérations élémentaires sur les lignes. Cela semble très compliqué mais en réalité ce n’est pas tant que ça, cependant toute une procédure doit être appliquée, donc si vous êtes plus intéressé vous pouvez chercher comment inverser une matrice dans le moteur de recherche de la page web (en haut à droite).
Enfin, la matrice d’Identité est également utile pour diagonaliser une matrice et calculer ses valeurs propres (ou valeurs propres). Parce qu’au moyen de certaines opérations, dans lesquelles la matrice unitaire intervient, le polynôme caractéristique à partir duquel les valeurs propres sont obtenues peut être obtenu. Mais c’est déjà un sujet très avancé, c’est pourquoi nous avons toute une page super complète dédiée à la diagonalisation des matrices avec des exemples et des exercices résolus l’expliquant. Si vous êtes plus intéressé, vous pouvez rechercher ce guide dans notre moteur de recherche (en haut à droite).