Sur cette page, vous trouverez une explication de ce que sont les lignes concurrentes, ainsi que des exemples de lignes concurrentes.
Que sont les lignes concurrentes ?
La définition mathématique des lignes concurrentes est la suivante :
En géométrie, les lignes concurrentes sont deux ou plusieurs lignes coplanaires qui se croisent au même point (appelé le point de concurrence). Par conséquent, un ensemble de lignes concurrentes n’a qu’un seul point en commun.
Si nous travaillons dans le plan (en R2) deux droites différentes ne peuvent être que coïncidentes, parallèles ou sécantes. Ainsi toutes les droites sécantes sont aussi des droites concurrentes, puisqu’elles ont un point d’intersection .
Si le concept précédent ne vous a pas été clair, je vous recommande de jeter un œil à la définition des lignes qui se croisent , où vous trouverez ce que sont ces types de lignes et comment savoir si deux lignes se croisent ou non.
En revanche, lorsqu’on opère dans l’espace (en R3) il est plus difficile de trouver des droites concurrentes, car il est plus compliqué que 2, 3, 4,… droites se coupent en un même point et, de surcroît, soient contenues dans un même plan.
D’autre part, le concept de concurrence ne s’applique pas seulement aux lignes : si deux ou plusieurs objets géométriques différents partagent un point, cela signifie qu’ils sont concurrents.
Exemple de lignes concurrentes
Une fois que nous avons vu la signification des lignes concurrentes, voyons maintenant un exemple de ce type de lignes :
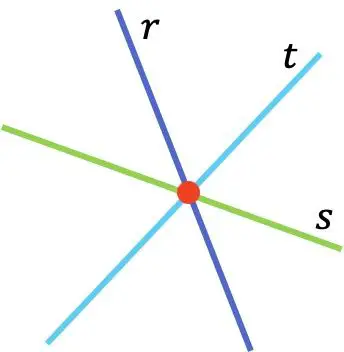
Comme vous pouvez le voir dans la représentation graphique des droites r, s et t, les trois droites sont concourantes car elles se coupent au même point (représenté en rouge).
Par contre, avant de terminer, si cette page vous a plu, vous vous intéressez peut-être aussi aux lignes droites en général. Eh bien, un concept très important à propos des lignes est de calculer leur équation, en fait, en géométrie analytique, les équations de la ligne sont très souvent utilisées. Vous pouvez voir comment cette équation se trouve sur la page suivante : comment calculer l’ équation de la droite qui passe par deux points .