Quel est le nombre d’Euler ?

Le nombre d’Euler (également connu sous le nom de constante d’Euler) est un nombre mathématique important et essentiel dans divers domaines des mathématiques, notamment la théorie des nombres, la topologie, la théorie des groupes et la théorie des fonctions. Il est représenté par la lettre grecque « e » et sa valeur approximative est de 2,71828.

Le nombre e découle de la formule de la fonction exponentielle et est un nombre fondamental dans la théorie des nombres complexes.

C’est aussi un nombre naturel qui apparaît dans la résolution de nombreux problèmes mathématiques, y compris le calcul des probabilités et la modélisation des processus de croissance et de décroissance.

Quelle est l’origine du nombre d’Euler ?

Le nombre d’Euler porte le nom du mathématicien suisse Leonhard Euler (1707-1783), qui fut l’un des plus grands mathématiciens de tous les temps et est considéré comme le père des mathématiques modernes.

Euler a apporté de précieuses contributions dans de nombreux domaines des mathématiques, notamment la théorie des nombres, la géométrie, le calcul, la physique et l’astronomie.

C’est lui qui a le premier défini et utilisé le nombre e (appelé nombre d’Euler) dans ses travaux sur le calcul et la théorie des logarithmes. La formule d’Euler pour les nombres complexes est également l’une de ses contributions les plus notables aux mathématiques.

Comment cette valeur est-elle obtenue ?

En fait, il existe plusieurs méthodes pour calculer le nombre d’Euler. Cependant, il convient de mentionner qu’aucune des deux méthodes ne donne un résultat exact. Par conséquent, sa numérotation est continue et infinie, mais elle n’est pas répétée.

En fait, à l’heure actuelle, plus de 1 billion de nombres sont connus qui composent la figure du nombre e. La série infinie qui définit le nombre d’Euler est :

Où “!” est factoriel, qui est défini comme le produit de tous les nombres naturels jusqu’à ce nombre. Par exemple:

5 ! = 5 4 3 2 1 = 120

Nous pouvons voir graphiquement cette série comme la somme d’une série de rectangles de hauteur 1 et de largeur décroissante, où la largeur de chaque rectangle est 1/n!, où n est le nombre de factorielles.

Si nous augmentons le nombre de rectangles dans la somme, l’approximation de l’aire sous la courbe de la fonction exponentielle se rapproche de plus en plus du nombre d’Euler.

En résumé, le nombre d’Euler est un nombre qui résulte de la somme d’une série infinie et qui est fondamental dans de nombreux domaines des mathématiques. Bien qu’il s’agisse d’un nombre irrationnel , sa valeur approximative est de 2,71828.

Il est important de garder à l’esprit qu’Euler lui-même a mis en œuvre cette méthode pour calculer e à 18 décimales.

Une autre façon de le calculer :

On peut calculer la valeur approchée du nombre d’Euler sur une droite à l’aide d’une série de termes finis . Par exemple, si l’on prend la première série infinie définie ci-dessus :

Nous pouvons calculer la valeur approximative en ajoutant les premiers termes de la série. Par exemple, si on additionne les 6 premiers termes :

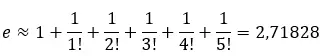
Nous pouvons tracer cette série sur une ligne pour voir comment elle se rapproche de la valeur approximative de 2,71828 .

Graphiquement, la ligne représentant le nombre d’Euler peut être tracée comme une série de rectangles de hauteur 1 et de largeur décroissante, où la largeur de chaque rectangle est 1/n!, où n est le nombre de factorielles.

Si nous augmentons le nombre de rectangles dans la somme, l’approximation de l’aire sous la courbe de la fonction exponentielle se rapproche de plus en plus du nombre d’Euler.

Équations exponentielles avec le nombre d’Euler

Les équations exponentielles avec le nombre d’Euler peuvent être utilisées pour modéliser une grande variété de phénomènes dans les sciences telles que la physique, la biologie, l’économie, entre autres. Voici quelques exemples :

Croissance et décroissance exponentielle

Ce modèle décrit la vitesse à laquelle une population croît ou diminue , ou la vitesse à laquelle une substance toxique se décompose.

Par exemple, si une population croît à un taux de 5 % par an, sa taille peut être décrite par la formule :

P(t) = P0 · e ^0,05t , où P0 est la taille initiale de la population.

Modèles de désintégration radioactive

Ce modèle décrit la vitesse à laquelle les atomes radioactifs se désintègrent dans le temps.

La formule est la suivante :

N(t) = N0 e ^-λt

où N0 est le nombre initial d’atomes, λ est une constante qui dépend de la matière radioactive et t est le temps.

Ce ne sont que quelques exemples de la façon dont les équations exponentielles avec le nombre d’Euler peuvent être utilisées dans la pratique. Il existe de nombreux autres domaines où les équations exponentielles sont utiles et pertinentes.

Quelles sont les applications du nombre d’Euler ?

Le nombre d’Euler a un large éventail d’applications dans différents domaines des mathématiques et des sciences. Certains des champs dans lesquels le nombre e est utilisé sont les suivants :

• Calcul et analyse mathématique : il est utilisé dans l’étude des fonctions exponentielles et logarithmiques, et dans la résolution des équations différentielles.
• Théorie des nombres – utilisée dans l’étude de la distribution des nombres premiers et dans la résolution de problèmes liés à la théorie des nombres.
• Probabilité et statistique : elle est utilisée dans la résolution de problèmes liés à la distribution de probabilité et dans l’estimation des valeurs attendues.
• Cryptographie – Utilisé dans l’étude des algorithmes de cryptage et de décryptage.
• Physique – utilisé pour résoudre des problèmes liés à la thermodynamique, à la mécanique quantique et à la physique statistique.
• Chimie : elle est utilisée dans la résolution de problèmes liés à la thermodynamique chimique et à la cinétique chimique.

Formule d’Euler pour les nombres complexes

La formule d’Euler pour les nombres complexes établit une relation entre les fonctions trigonométriques et exponentielles. La formule s’écrit :

Où “e” est la base des logarithmes naturels, “i” est l’unité imaginaire, “x” est un nombre réel et “cos” et “sin” sont respectivement les fonctions trigonométriques cosinus et sinus.

Cette formule est très utile dans de nombreux domaines des mathématiques, y compris la théorie des nombres, la théorie des fonctions et la théorie de la complexité, et a une grande variété d’applications en ingénierie, physique et économie.

Un exemple pratique de son utilisation est dans la représentation des signaux et des systèmes dans l’analyse de Fourier, dans laquelle les signaux périodiques sont représentés comme une somme de signaux sinusoïdaux complexes.

La formule d’Euler est utilisée pour décrire comment ces signaux complexes sont liés aux fonctions trigonométriques réelles qui décrivent les signaux sinusoïdaux individuels.

Le nombre d’Euler et l’intérêt composé

L’intérêt composé est un concept financier qui décrit le processus par lequel une somme d’argent, appelée principal, génère des intérêts sur les intérêts accumulés au fil du temps.

En d’autres termes, les intérêts générés par un investissement proviennent non seulement du capital initial, mais également des intérêts générés au cours des périodes précédentes.

Le nombre d’Euler et l’intérêt composé sont liés car la formule de calcul de l’intérêt composé utilise le nombre d’Euler. La formule des intérêts composés est :

A = P e ^rt

Où A est le montant final, P est le principal, r est le taux d’intérêt, t est le temps et e est le nombre d’Euler. De cette façon, le nombre d’Euler est un facteur important dans la formulation mathématique pour le calcul de l’intérêt composé.

Un exemple de calcul d’intérêts composés avec des nombres concrets serait le suivant :

Supposons que nous ayons un investissement de 1 000 € à un taux d’intérêt de 5 % par an pendant 2 ans. La formule pour calculer les intérêts composés serait :

A = P e ^rt = 1000 e ^{0,05 2} = 1000 1,1025 = 1102,5 €.

Cela signifie qu’après 2 ans, notre capital initial de 1 000 € sera passé à 1 102,5 € grâce aux intérêts composés générés.

Exemples d’exercices mathématiques avec le nombre d’Euler

Voici deux exemples de problèmes mathématiques résolus impliquant le nombre d’Euler :

1. Trouvez la valeur de “e ^ix ” où x est un nombre réel :

L’identité d’Euler nous dit que e ^ix = cos(x) + i · sin(x). Par conséquent, si nous connaissons la valeur de x, nous pouvons calculer la valeur de e ^ix en utilisant les fonctions trigonométriques.

2. Calculez e^(x ² ) pour une valeur donnée de x :

Nous pouvons utiliser la série de Taylor pour calculer la valeur de e^(x ² ). La série de Taylor de e ^x est un développement infini qui permet de calculer des approximations successives de la valeur de e ^x , selon le terme utilisé.

Si nous substituons x ² à x dans cette série, nous obtenons la série de Taylor pour e^(x ² ).