이 페이지에서는 행렬을 더하고 빼는 방법을 살펴보겠습니다. 완벽하게 이해하는 데 도움이 되는 예문도 있고, 연습할 수 있도록 문제도 풀었습니다. 또한 행렬 추가의 모든 속성을 찾을 수 있습니다.
행렬을 더하고 빼는 방법은 무엇입니까?
두 행렬의 덧셈(또는 뺄셈)을 계산하려면 행렬에서 동일한 위치를 차지하는 요소를 더하거나 빼야 합니다.
예:

두 행렬을 더하거나 빼려면 차원이 동일해야 합니다. 예를 들어 다음 행렬은 첫 번째 행렬이 2×2 행렬이고 두 번째 행렬이 3×2 행렬이므로 추가할 수 없습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-082c648e15685c4ddeac2cc2da502d96_l3.png)
행렬의 덧셈과 뺄셈을 위한 해결된 연습문제
연습 1
다음과 같은 2×2 행렬의 합을 계산합니다.
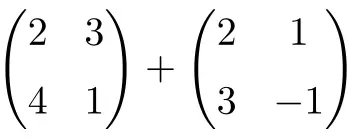
이는 2×2 차원의 두 정사각 행렬의 합입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d9428ad89a6bd149d5e63bc500879ac_l3.png)
연습 2
다음 행렬 빼기를 수행합니다.
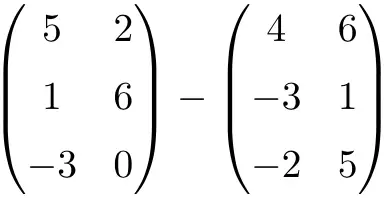
이는 3×2 차원의 두 행렬을 빼는 것입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c371e1f01df59f4b8abb018e476e66d7_l3.png)
연습 3
3×3 차원의 다음 행렬 합의 결과를 구합니다.
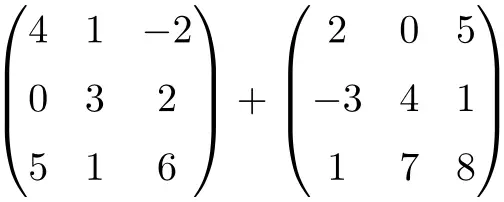
이는 3×3 차수의 두 정사각 행렬의 합입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-280299cb0b37e1a585466c4570439ec4_l3.png)
연습 4
2차 정사각 행렬의 다음 덧셈과 뺄셈을 계산합니다.
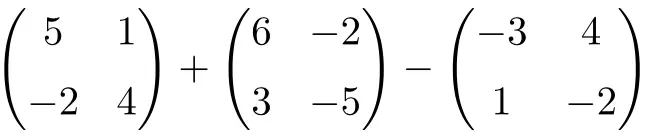
이는 2차 정사각 행렬의 덧셈과 뺄셈이 결합된 연산입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9fa4dba7699c0035ce5081756b4f62e_l3.png)
먼저 왼쪽에 행렬을 추가합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e1544e4da9d5ad2ea3ec2e4ad0326023_l3.png)
그런 다음 행렬의 뺄셈을 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd7f32fc7c9429fdfc3b5b745e85975c_l3.png)
연습 5
다음 행렬 덧셈과 뺄셈을 풀어보세요.
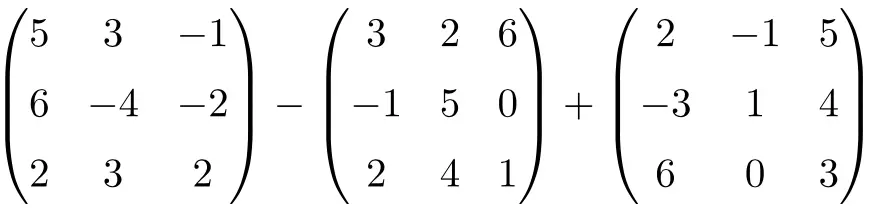
이는 3차 정사각 행렬의 뺄셈과 덧셈을 결합한 연산입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae66268adcd61258654056815542cf58_l3.png)
먼저, 행렬 빼기를 푼다:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4401b28babce2beaaa6f840c4ed8c959_l3.png)
그리고 마지막으로 행렬을 추가합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffba1ade3d98c434960b54fc0c7ffe1f_l3.png)
이제 행렬을 더하고 빼는 방법을 알았으니 행렬 연산 중 가장 중요한 행렬 곱셈 방법을 알아보겠습니다. 또한 이 사이트의 모든 페이지에서와 같이 연습할 수 있도록 해결된 단계별 행렬 곱셈 연습도 찾을 수 있습니다. 😉
행렬 속성 추가
행렬 추가에는 다음과 같은 특징이 있습니다.
- 행렬 덧셈에는 교환 특성이 있습니다.
![]()
따라서 행렬을 추가하는 순서는 동일합니다. 이를 시연하기 위해 순서를 변경하여 두 개의 행렬을 추가하고 결과가 어떻게 동일한지 확인합니다.
따라서 우리는 특정 순서로 두 개의 행렬을 추가합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7eb454436dc3268ae8d6d2b62f395a7_l3.png)
행렬의 덧셈 순서를 반대로 바꿔도 결과는 동일하게 유지됩니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c1e9cd77bc490913ed30ff63815da355_l3.png)
- 행렬 덧셈의 또 다른 속성은 반대 요소의 속성입니다.
![]()
즉, 동일한 행렬에 모든 요소의 부호가 변경된 행렬을 추가하면 결과는 0 행렬이 됩니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-add832e83fe554143cbd4c710315c1c0_l3.png)
- 행렬 덧셈에는 중립 요소 속성도 있습니다.
![]()
이 속성은 가장 명백하며, 모든 행렬에 0으로 가득 찬 행렬을 더하면 동일한 행렬과 동일하다는 사실을 나타냅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac7b0ba246075c196188798be2c6a034_l3.png)
- 행렬 덧셈에는 다음과 같은 결합 속성이 있습니다.
![]()
따라서 행렬을 추가하는 순서는 동일합니다. 다음 예를 보세요. 순서가 다른 3개의 행렬을 추가하면 결과가 동일합니다.
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bae8e10bca43351f3a84f83bfe50ab55_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2cc2b7a14cacc7e403cd729cd863d309_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab1f88e74b139451eccb0471988c3db_l3.png)