이 페이지에서는 평행사변형의 규칙(또는 법칙)에 대한 설명을 찾을 수 있습니다. 또한 평행사변형 규칙을 사용한 벡터 덧셈과 뺄셈의 몇 가지 예와 실제 적용 사례를 볼 수 있습니다.
평행사변형의 법칙이 무엇인가요?
이미 알고 있듯이 벡터 양은 실수와 같은 방식으로 더하거나 뺄 수 없습니다. 왜냐하면 벡터에는 2개의 구성요소(R2에서) 또는 3개의 구성요소(R3에서)가 있고 벡터의 방향이 다를 수 있기 때문입니다. 따라서 벡터 연산을 수행하려면 다음과 같이 구성된 평행사변형 규칙과 같은 다른 방법이 필요합니다.
수학에서 평행사변형 규칙은 그래픽 표현에서 두 벡터를 더하거나 빼는 절차입니다.
평행사변형 방법은 사용하기 매우 쉬운 기술이기 때문에 (그래픽적으로) 벡터의 덧셈과 뺄셈에 가장 많이 사용됩니다. 예를 들어, 물리학에서는 힘을 더하고 빼는 데 사용됩니다.
한편, 벡터를 더할 것인지 빼려는 것인지에 따라 규칙이 조금씩 달라지므로 아래에서는 두 버전을 별도로 설명하겠습니다.
두 벡터를 더하는 평행사변형 규칙
그래픽적으로 두 개의 벡터를 추가하려는 경우 평행사변형 규칙 또는 법칙을 적용하는 단계는 다음과 같습니다.
- 먼저 벡터를 그리고 동일한 적용 지점에 배치합니다. 즉, 두 벡터의 원점을 동일한 지점에 배치합니다.
- 그런 다음 한 벡터의 끝에 다른 벡터와 평행한 선을 그립니다. 그리고 다른 벡터로 이 단계를 반복합니다. 따라서 우리는 평행사변형의 그림을 얻을 것입니다(따라서 규칙의 이름).
- 마지막으로, 합의 결과인 벡터는 벡터의 공통 원점에서 두 평행선의 교차점까지 이동하는 평행사변형의 대각선이 됩니다.
다음의 일반적인 예에서는 평행사변형 규칙이 사용되는 방법을 볼 수 있습니다.

평행사변형 규칙을 연습하고 싶다면 다음 링크에서 더 많은 예제와 여러 벡터 덧셈 연습 문제를 참고할 수 있습니다. 이 페이지에서는 벡터를 그래픽으로 추가하는 다른 방법과 벡터를 수치적으로 추가하는 방법도 찾을 수 있습니다.
두 벡터를 빼는 평행사변형 규칙
평행사변형 규칙 또는 방법은 그래프에서 두 벡터를 빼는 데에도 사용됩니다. 따라서 벡터 빼기 단계는 다음과 같습니다.
- 먼저, 그래프에 두 벡터를 나타내고 이를 동일한 적용 지점에 배치합니다. 즉, 두 벡터의 원점을 동일한 지점에 배치합니다.
- 둘째, 연산에서 빼는 벡터의 반대 벡터를 그린다. 즉, 빼는 벡터를 반전시킨다.
- 그런 다음 벡터 끝에 부호 변경 벡터와 평행한 선을 그립니다. 그리고 우리는 다른 벡터로 이 과정을 반복합니다. 그래서 우리는 평행사변형의 그림을 얻을 것입니다(따라서 규칙의 이름).
- 마지막으로 뺄셈의 결과는 두 벡터의 공통 원점에서 두 평행선이 교차하는 지점까지 가는 벡터가 됩니다.
평행사변형 법칙에 따라 두 벡터를 빼는 다음의 일반적인 예를 살펴보십시오.
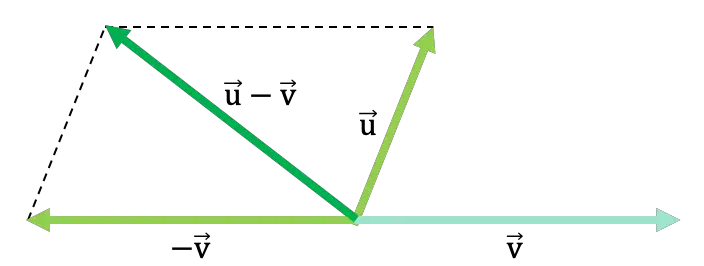
다음 링크에서 평행사변형 규칙을 사용한 벡터 뺄셈의 더 많은 예를 볼 수 있으며, 벡터 뺄셈 연습 문제를 풀어서 연습할 수도 있습니다. 또한 그래프에서 벡터를 빼는 다른 기술과 마지막으로 수치적으로 벡터를 빼는 방법도 확인할 수 있습니다.
마지막으로, 이 기술에 대한 설명이 도움이 되었다면 오른손 법칙이 무엇인지도 알고 싶을 것입니다. 링크 페이지에서 이것이 무엇인지, 어떤 벡터 연산에 사용되는지, 그리고 존재하는 이 규칙의 다양한 변형을 확인할 수 있습니다.