Pi라는 숫자는 원의 둘레와 지름 사이의 관계를 나타내는 수학 상수 입니다. 그것은 불합리한 숫자입니다. 즉, 정확한 분수가 아닙니다 . 따라서 유한십진수로 표현할 수 없습니다. Pi의 값은 대략 3.14159이며 그리스 문자 π로 표시됩니다.
파이는 수학에서 중요한 숫자이다. 따라서 다양한 분야에 많은 응용이 가능합니다. 예를 들어 기하학에서 면적을 계산하는 데 사용됩니다. 또한 원 및 기타 원형 도형의 둘레입니다. 반면에 삼각법에서는 호의 각도와 길이를 계산합니다. 마지막으로 공학 및 물리학에서는 부피 및 용량과 같은 수량을 계산합니다.
파이데이는 매년 3월 14일을 파이(Pi) 값(3.14)에 가깝기 때문에 기념하는 날이다. 이 날짜는 수학에서 Pi의 역할을 기념하고 이 기본 상수에 대한 관심을 높이기 위해 기념되었습니다.
Pi라는 숫자를 발견한 사람은 누구일까요?
파이라는 수는 고대부터 알려져 왔으며, 이를 정확하게 기술한 사람은 그리스 수학자 아르키메데스(기원전 287~212년)였습니다. 실제로 그는 기하학적 도형의 면적과 부피를 계산하는 데 이를 사용했습니다.
18세기에 스위스 수학자 요한 램베르트는 파이가 무리수 라는 것을 증명했습니다. 그 후 19세기에 독일의 수학자 페르디난트 폰 린데만(Ferdinand von Lindemann)은 파이(Pi)가 초월수 라고 설명했습니다. 즉, 유리계수를 갖는 다항방정식의 정확한 해로 표현될 수 없다.
역사를 통틀어 다양한 수학자들이 숫자 Pi를 이해하는 데 기여했으며 이를 더 정확하게 계산하는 기술을 개발했습니다. 오늘날 Pi는 세계에서 가장 중요하고 가장 잘 알려진 수학 상수 중 하나로 남아 있으며 계속해서 수학 연구 주제가 되고 있습니다.
Pi라는 숫자는 왜 무한합니까?
Pi의 값은 대략 3.14159이지만 실제로는 소수점 이하까지 무한정 계속되는 숫자이다. 이는 Pi가 무한한 숫자이며 십진수로 완전히 표현될 수 없음을 의미합니다.
Pi의 값은 무한하지만 실제로는 Pi의 대략적인 값을 매우 정확하게 계산할 수 있습니다. 지금까지 수백만 자릿수의 Pi가 계산되었으며 십진수에 규칙적인 패턴이 없는 것으로 나타났습니다. 하지만 우리는 그렇게 많은 숫자를 계산할 수 없기 때문에 슈퍼컴퓨터를 통해 수행했습니다.
숫자 Pi의 대략적인 값을 계산하는 방법은 무엇입니까?
Pi 값을 계산하는 실용적인 방법에는 여러 가지가 있으며, 다음으로 수학자들이 가장 많이 사용하는 세 가지 방법을 단계별로 설명합니다.
1. 아르키메데스의 방법
그리스 수학자 아르키메데스는 기하학적 방법을 사용하여 Pi의 대략적인 값을 계산했습니다. 이 방법을 사용하려면 다음 단계를 따르세요.
1. 원을 그리고 원의 중심을 통과하는 선을 그리고 아래와 같이 반대쪽 두 점에서 교차합니다.
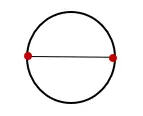
2. 원과 교차하는 선의 길이를 측정하고 “D”라고 표시합니다. 이 측정값은 원의 직경입니다.
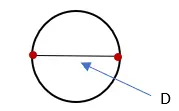
3. 원을 이루는 선의 길이를 측정하고 “C”라고 표시합니다. 이 측정값은 원의 둘레입니다.
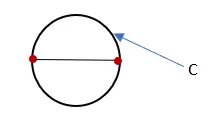
4. 원의 둘레(C)를 원의 지름(D)으로 나눕니다. 결과는 Pi의 대략적인 값입니다.
예를 들어 원의 지름이 6이고 원주가 18이라면 Pi의 대략적인 값은 18 ¼ 6 = 3입니다. 분명히 이 예는 매우 기본적이지만 실제 원주 값으로 수행한다면 , 메소드가 올바르게 작동하는 것을 볼 수 있습니다.
실제로 시도해 보시기 바랍니다. 컵이나 원형 모양의 물건을 측정하여 자신에게 맞는지 확인하세요.
2. 몬테카를로 방식
몬테카를로법은 Pi의 근사값을 계산하는 데 사용되는 확률론적 방법으로, 평면 위에 무작위로 많은 수의 점을 생성하고 정사각형에 내접하는 원 안에 들어맞는 점의 개수를 세는 방식이다. 프로세스는 다음과 같이 적용됩니다.
1. 아래와 같이 변 1의 정사각형 안에 원을 그립니다.

2. 사각형에 무작위로 많은 수의 포인트를 생성합니다.
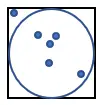
3. 원에 맞는 점의 개수를 셉니다. 이 수량을 “n”이라고 부르겠습니다.
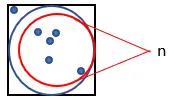
4. 생성된 총 포인트 수를 계산합니다. 이 수량을 “m”이라고 부르세요.
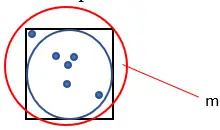
5. 다음 공식을 사용하여 Pi의 대략적인 값을 계산합니다. Pi = (4 · n) ¼ m.
예를 들어, 380개의 점이 생성되었고 300개가 원에 맞는 경우 Pi의 대략적인 값은 (4 · 300) ¼ 380 = 3.16입니다. 이 값은 Pi의 소수점 처음 두 자리와 많이 비슷해 보이지만 이전 방법과 마찬가지로 실제 측정값을 사용하면 훨씬 더 정확한 값을 얻을 수 있습니다.
3. 반복 방법
반복법은 Pi의 대략적인 값을 계산하는데 사용되는 수학적 방법으로, Pi의 값을 암시하는 공식을 사용하고 이를 반복적으로 적용하여 계산의 정확도를 향상시키는 방법이다. 이 방법을 사용하는 단계는 다음과 같습니다.
- Pi의 초기 값을 선택합니다. 예를 들어 값 3을 선택할 수 있습니다.
- Pi 값과 관련된 공식을 사용하여 새로운 대략적인 값을 계산합니다. 예를 들어, 다음 공식을 사용할 수 있습니다: Pi = (Pi + (4 ¼ Pi)) ¼ 2
- 새로운 대략적인 값을 이전 값과 비교합니다. 둘 사이의 차이가 충분히 작다면 정확한 결과에 도달한 것입니다. 차이가 여전히 큰 경우 Pi에 새 값을 할당하고 2단계부터 프로세스를 반복합니다.
예를 들어 Pi의 초기 값이 3인 경우 새 대략적인 값은 (3 + (4 ¼ 3)) ¼ 2 = 2.66666666이 됩니다. 하지만 둘 사이의 차이가 그리 작지 않기 때문에 정확한 값을 찾기 전에 언제든지 이 과정을 여러 번 반복할 수 있습니다.
숫자 Pi의 용도는 무엇입니까?
파이는 수학에서 중요한 숫자이며 다양한 분야에 응용 될 수 있습니다. Pi의 가장 중요한 응용 프로그램에는 다음이 있습니다.
기하학
Pi는 기하학에서 원과 기타 원형 도형의 면적과 둘레를 계산하는 데 사용됩니다.
- 원 : 원의 면적과 둘레를 계산합니다.
- 구 : 구의 면적과 부피를 결정합니다.
- 실린더 : 실린더의 표면적과 부피를 계산합니다.
- 원뿔 – 원뿔의 표면적과 부피를 계산하는 데 사용됩니다.
삼각법
각도와 호 길이를 계산하기 위한 삼각법에 유용합니다. 일부 응용 프로그램은 다음과 같습니다.
- 각도 : 각도 및 호 길이를 계산합니다.
- 삼각 함수 – 특정 각도에 대한 삼각 함수 값을 계산하는 데 사용됩니다.
- 원형 삼각법 : 360도 각도에 대한 삼각 함수 값을 계산합니다.
공학
엔지니어링에서 Pi는 부피 및 용량과 같은 수량을 계산하는 데 사용됩니다. 일부 응용 프로그램은 다음과 같습니다.
- 전자 장치 : 저항, 정전 용량 등의 수량을 계산합니다.
- 전기 : 전력, 전기에너지 등의 양을 계산하는데 사용됩니다.
- 토목공학 : 구조물, 건축요소의 표면적, 부피 등의 수량을 계산합니다.
물리적
파이(π)라는 숫자는 물리학에서 다양한 용도로 사용되는 수학 상수입니다. 다음은 물리학에서 Pi를 사용하는 몇 가지 예입니다.
- 파도 – 파도의 주파수와 파장을 계산하는 데 사용됩니다.
- 역학 : 역학에서는 회전계의 일과 에너지를 계산하는 데 유용합니다.
- 전자기학 : 전자기학에서는 커패시터에 저장된 에너지와 권선의 인덕턴스를 계산하는 데 사용할 수 있습니다.
- 우주론 우주론 에서 Pi는 시공간의 곡률과 우주의 팽창을 계산하는 데 사용됩니다.
Pi라는 숫자는 실생활에서 어떤 용도로 사용되나요?
다음은 Pi가 일상 생활에서 어떻게 사용되는지에 대한 몇 가지 예입니다.
- 기하학 : 원형 매트의 면적을 정의하거나 원형 테이블의 둘레를 덮는 데 필요한 줄자의 길이를 측정합니다.
- 요리 – 냄비를 채우는 데 물이나 액체가 얼마나 필요한지 또는 원형 용기에 들어갈 재료의 수를 결정합니다.
- 천문학 : 행성과 별 사이의 거리, 행성의 궤도, 하늘에 있는 천체의 위치를 알아보세요.
- 원예 : 원형 화분을 채우는 데 필요한 흙의 양을 알거나 원형 정원에서 식물에 물을 주는 데 필요한 물의 양을 계산합니다.