여기에서는 코사인 함수(공식)를 유도하는 방법을 알아봅니다. 코사인 함수의 미분 예를 확인하고 단계별 연습을 통해 연습할 수 있습니다. 또한, 코사인의 2차 도함수는 무엇인지, 심지어 역코사인의 도함수는 무엇인지에 대한 공식의 증명도 보여드립니다.
코사인의 미분은 무엇입니까?
코사인 함수의 미분은 부호 수정된 사인 함수입니다. 즉, x의 코사인의 도함수는 x의 사인을 뺀 값과 같습니다.
![]()
코사인 인수에 함수가 있는 경우 코사인의 도함수는 해당 함수의 사인을 뺀 값에 함수의 도함수를 곱한 값입니다.
![]()
두 번째 공식은 첫 번째 공식과 동일하지만 체인 규칙을 적용합니다. 따라서 요약하면 코사인의 미분 공식은 다음과 같습니다.
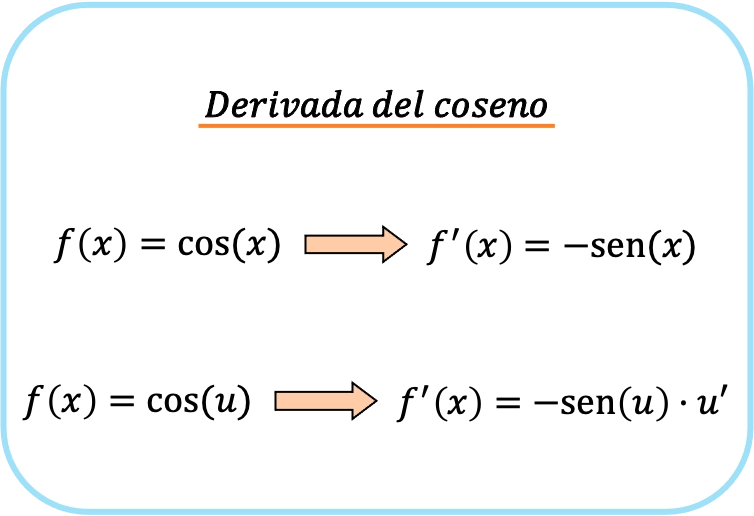
코사인 파생 예
이제 우리는 코사인 공식이 무엇인지 알았으므로 이러한 유형의 삼각 함수 미분에 대한 몇 가지 예를 설명하여 코사인 함수를 파생하는 방법에 대해 의심의 여지가 없습니다.
예시 1: 2x의 코사인 파생
![]()
코사인 인수에는 단일 x가 없고 오히려 더 복잡한 함수가 있습니다. 따라서 코사인을 도출하려면 다음 공식을 사용해야 합니다.
![]()
2x의 도함수는 2이므로, 2x의 코사인의 도함수는 2x의 사인에서 2를 곱한 값을 뺀 값이 됩니다.
![]()
예 2: x 제곱의 코사인 파생
![]()
이전 예에서와 같이 코사인 인수에는 x와 다른 함수가 있으므로 체인 규칙을 사용하여 코사인을 파생합니다.
![]()
그러면 x 2 의 도함수는 2x입니다. 따라서 x의 2승 코사인 도함수는 다음과 같습니다.
![]()
예시 3: 세제곱 코사인의 미분
![]()
이 예의 코사인 함수는 다른 함수로 구성되어 있으므로 도함수를 풀려면 다음 공식을 적용해야 합니다.
![]()
따라서 공식을 적용하여 함수의 미분에 도달합니다.
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73284bcfb1d5647b2304e323e7fbaedf_l3.png)
➤ 이 함수를 미분하려면 잠재적 함수의 도함수 공식도 사용해야 합니다.
코사인의 2차 도함수
다음으로 삼각함수의 특성으로 인해 사인의 2차 도함수를 쉽게 계산할 수 있음을 알아보겠습니다.
➤ 참고: 다음 내용을 이해하려면 사인의 도함수가 무엇인지 알아야 합니다 .
x의 코사인의 2차 도함수는 x의 코사인을 뺀 값입니다. 이상하게 보일 수도 있지만 수학적으로는 그렇습니다. 실제로 사인의 도함수는 코사인이므로 x의 코사인을 두 번 미분하면 코사인이 다시 얻어지지만 부호는 수정됩니다.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0d9dda8a4031c367120b1f950da4391_l3.png)
이 속성은 코사인 인수가 x가 아닌 경우 변경됩니다. 이 경우 체인 규칙의 항을 드래그하기 때문입니다.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83d86bd6508f06b0723153b3b9254c1f_l3.png)
역코사인의 미분
모든 삼각함수는 역함수를 가지므로 코사인 함수도 역함수가 가능합니다. 마찬가지로, 역코사인은 미분 가능합니다.
함수 의 역코사인의 도함수는 함수의 도함수를 1의 제곱근에서 해당 함수의 제곱을 뺀 값으로 나눈 값입니다.
![]()
역코사인은 아크코사인이라고도 합니다.
예를 들어, 3x의 역코사인의 미분은 다음과 같습니다.
![]()
코사인의 미분에 대한 해결 연습
다음 코사인 함수의 미분을 계산합니다.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f4645fb77435daec6f696cffbd54884_l3.png)
코사인 파생물의 증명
마지막으로 x의 코사인 도함수 공식을 수학적으로 설명하겠습니다. 이를 위해 다음 극한에 해당하는 미분의 정의를 사용합니다.
![]()
우리는 코사인을 증명할 것이므로 함수는 cos(x)입니다:
![]()
결국 불확정 상태가 되기 때문에 대체를 통해 이 제한을 해결할 수 없습니다. 그러나 다음 삼각법 항등식을 적용하여 합의 코사인을 다른 방식으로 표현할 수 있습니다.
![]()
![]()
다음 단계는 분수를 두 개의 분수로 분리하고 코사인의 공통 인수를 취하는 것입니다.
![Rendered by QuickLaTeX.com \displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-c7c1cd89cf290b01d7d72fc8084f6529_l3.png)
뺄셈의 극한은 극한의 뺄셈과 같습니다. 따라서:
![]()
x의 코사인과 x의 사인은 h에 의존하지 않으므로 범위 밖으로 추출할 수 있습니다.
![]()
무한소 등가물에 의한 극한 계산을 사용하여 첫 번째 극한은 0이고 두 번째 극한은 1이라고 결론을 내립니다. 따라서:
![]()
![]()
그리고 우리는 이미 코사인 함수의 미분 공식에 도달했으므로 동등성이 입증되었습니다.