이 페이지에서는 정사각 행렬이 무엇인지 설명하고 정사각 행렬의 예를 찾을 수 있습니다. 또한 정사각형 행렬의 속성, 이를 사용하여 수행할 수 있는 연산 및 존재하는 다양한 유형을 확인할 수 있습니다.
정사각 행렬이란 무엇입니까?
정사각 행렬 은 행의 개수와 열의 개수가 같은 행렬.
정사각 행렬의 예
2차 정사각 행렬
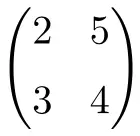
3차 정사각 행렬
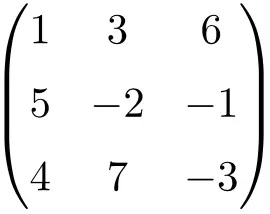
4차 정사각 행렬
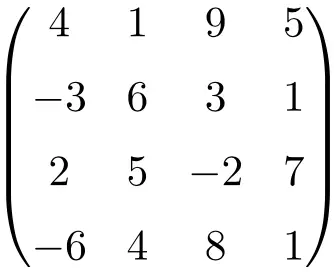
보시다시피, 정사각 행렬은 일반적으로 순서에 따라 이름이 지정됩니다. 즉, 2차 정사각 행렬은 차원 2×2(2행 2열)의 행렬을 의미하거나 3차 정사각 행렬을 의미합니다. 이는 크기가 3×3(행 3개, 열 3개)임을 나타냅니다.
정사각 행렬의 대각선
정사각 행렬의 대각선에는 특정 이름이 있으며 주 대각선과 보조 대각선이 있습니다.
- 정사각 행렬의 주대각선은 왼쪽 위 모서리에서 오른쪽 아래 모서리로 이동하는 요소로 구성됩니다.

- 정사각 행렬의 2차 대각선은 왼쪽 아래 모서리에서 오른쪽 위 모서리로 이동하는 요소에 해당합니다.

정사각 행렬의 속성
정사각형 행렬은 선형 대수학에서 널리 사용되므로 이것이 매우 중요합니다. 그러면 이 행렬 클래스를 관련성 있게 만드는 특성이 무엇인지 살펴보겠습니다.
- 모든 정사각 행렬은 대칭 행렬 과 반대칭 행렬 의 합으로 분해될 수 있습니다.
- 두 개의 정사각 행렬이 동일한 순서인 경우 서로 더하거나 뺄 수 있습니다.
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- 두 개의 정사각형 행렬은 가능한 두 방향으로 곱해질 수 있습니다 . 그러나 정사각 행렬의 곱은 교환 가능하지 않습니다. 즉, 어느 쪽을 곱하느냐에 따라 곱셈 결과가 달라집니다. 다음 예에서 결과가 행렬의 위치에 따라 어떻게 달라지는지 확인하세요.
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- 정사각형 행렬은 행렬식을 계산할 수 있는 유일한 행렬입니다. 따라서 행렬식은 정방행렬인 경우에만 풀 수 있습니다 . 예를 들어, 3×3 정사각 행렬의 행렬식을 찾으려면 Sarrus의 규칙을 적용해야 합니다.
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
또한 행렬식의 행렬식이 0과 다르다면 이는 정규행렬 , 즉 가역행렬이라는 뜻임을 기억하자. 반면, 행렬식이 0이면 역행렬이 없는 특이 행렬 입니다.
- 마지막으로, 정사각형 행렬은 대각화될 수 있습니다 . 따라서 밑변환을 수행하여 정사각 행렬의 고유값(또는 고유값)과 고유벡터(또는 고유벡터)를 계산할 수 있습니다.
정사각 행렬을 사용한 연산
우리가 본 것처럼 행렬의 행렬식은 행렬이 정사각형인 경우에만 계산할 수 있습니다. 마찬가지로, 행렬이 제곱 차원인 경우에만 수행할 수 있는 특정 작업도 있습니다.
매트릭스의 흔적
행렬의 자취는 정사각 행렬의 주대각선을 구성하는 요소의 합입니다.
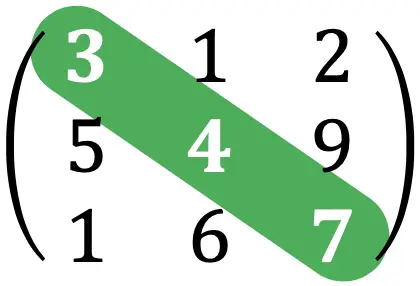
예를 들어 위 연습의 행렬 추적은 다음과 같습니다.
![]()
사각 다이의 종류
그러면 존재하는 가장 중요한 유형의 정사각형 행렬이 있습니다. 다이 유형을 클릭하면 다이의 특별한 점을 확인할 수 있습니다.

삼각행렬

대각행렬

매트릭스 항등

대칭행렬
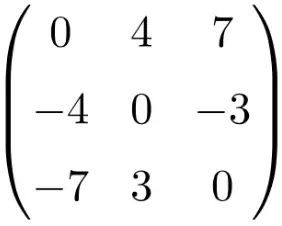
비대칭 행렬
보시다시피, 정사각 행렬에는 다양한 유형이 있으며 각 행렬은 서로 다른 이유로 고유한 이름을 갖습니다.