이번 글에서는 곡선의 접선 방정식을 구하는 방법을 알아보겠습니다. 또한, 다양한 난이도의 해결된 연습문제를 통해 훈련할 수 있습니다.
한 점에서 함수에 대한 접선의 방정식
x=x 0 지점에서 함수 f(x)에 대한 접선 방정식은 다음과 같습니다.
![]()
여기서 P(x 0 ,y 0 ) 지점은 접선과 함수가 일치하는 지점입니다. 그리고 접선의 기울기 m은 x 0 지점에서 곡선의 도함수와 같습니다. 즉, m=f'(x 0 )입니다.

위 이미지에서 곡선을 볼 수 있습니다
![]()
파란색과 함수에 접하는 주황색 선으로 표시됨
![]()
에 대한
![]()
, 이 점만 공통점이 있기 때문입니다. 음, 이 탄젠트의 방정식은 다음과 같습니다.
![]()
이고 그 기울기는
![]()
.
탄젠트 방정식을 찾는 방법
한 점에서 함수에 대한 접선 방정식을 찾으려면 다음을 수행해야 합니다.
- 접선 지점에서 함수의 도함수를 계산하여 접선의 기울기를 찾습니다.
- 접선 위의 점을 결정합니다.
- 계산된 기울기와 접선의 점을 이용하여 접선의 방정식을 구합니다 .
곡선에 대한 접선 방정식의 예
탄젠트 방정식에 대한 이론을 살펴본 후에는 예제를 단계별로 풀어 탄젠트 방정식을 계산하는 방법을 살펴보겠습니다.
- 곡선에 대한 접선의 방정식을 계산합니다.
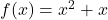
에 대한
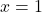
.
우리는 탄젠트 방정식이 항상 다음과 같은 형식이라는 것을 알고 있습니다.
![]()
가장 먼저 할 일은 선의 기울기를 계산하는 것입니다. 따라서 접선의 기울기는,
![]()
는 접선 x=1 지점에서 곡선의 도함수 값이 됩니다. 즉
![]()
따라서 우리는 함수를 미분한 다음 계산합니다.
![]()
![]()
![]()
![]()
우리가 그 가치를 알고 나면
![]()
, 우리는 요점을 찾아야 해요
![]()
접선 방정식을 완성하려면 접선을 사용하세요.
접선과 곡선의 방정식에는 항상 공통점이 있는데 , 이 경우에는
![]()
. 그러므로 곡선처럼
![]()
이 점을 통과하면 다음을 계산하여 점의 다른 구성 요소를 찾을 수 있습니다.
![]()
![]()
![]()
따라서 접선점은 다음과 같습니다.
![]()
곡선과 접선 모두 이 점을 통과하므로 이를 사용하여 접선의 방정식을 찾을 수도 있습니다.
남은 것은 발견된 기울기 값과 접선 점을 방정식으로 대체하는 것입니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0321e19825c08a1f47a00b2cf625088f_l3.png)
즉, 접선 방정식은 다음과 같습니다.
![]()
또한 선의 명시적 방정식을 사용하여 접선의 방정식을 표현할 수도 있습니다.
![]()
아래에서 곡선이 표현된 것을 볼 수 있습니다.
![]()
그리고 그것의 접선은
![]()
![]()
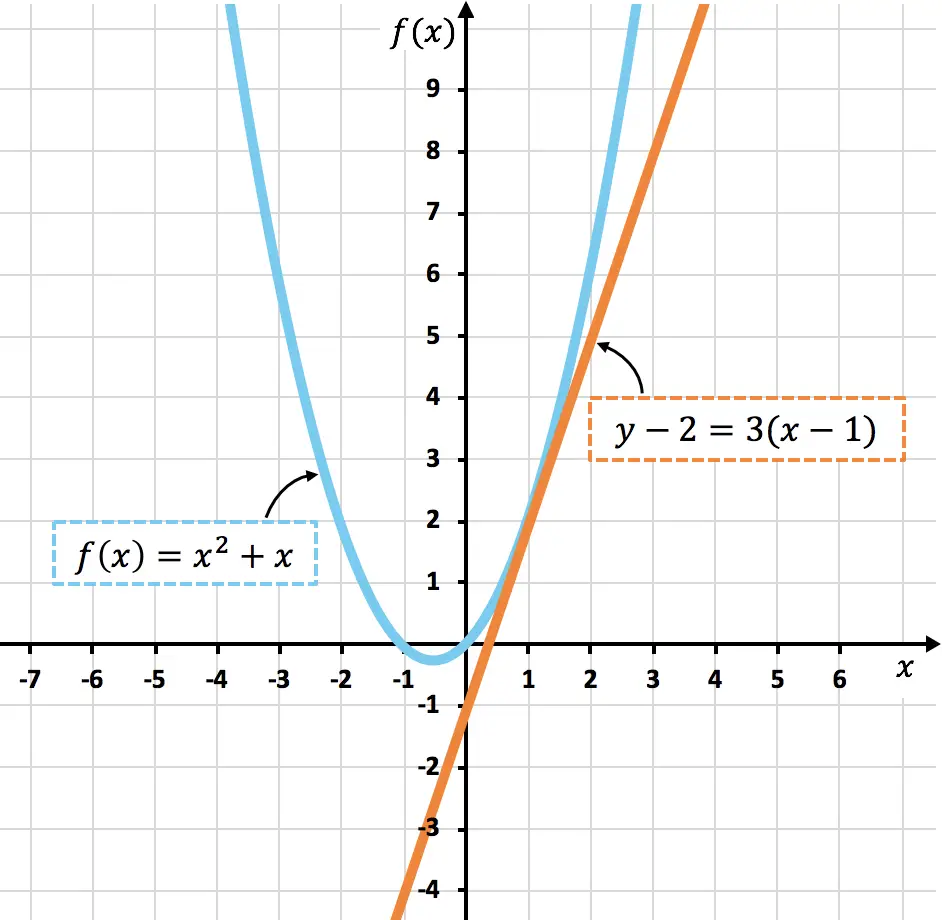
보시다시피 곡선이
![]()
그리고 접선
![]()
그 사람들의 공통점은 딱 하나야
![]()
, 정확히 우리가 계산한 대로입니다.
접선 방정식에 대한 해결 연습
연습 1
곡선에 대한 접선의 방정식을 계산합니다.
![]()
에 대한
![]()
접선 방정식은 항상 다음 형식을 따릅니다.
![]()
1단계: 접선의 기울기 계산
기울기 m 은 접선 지점에서 곡선의 도함수 값입니다. 따라서 이 경우
![]()
![]()
![]()
![]()
2단계: 접선에서 점 찾기
접선과 곡선의 방정식에는 항상 공통점이 있는데, 이 경우에는
![]()
. 그러므로 곡선처럼
![]()
이 점을 통과하면 다음을 계산하여 점의 다른 구성 요소를 찾을 수 있습니다.
![]()
![]()
![]()
따라서 곡선과 접선이 모두 통과하는 점이 점입니다.
![]()
3단계: 접선 방정식 작성
남은 것은 발견된 기울기 값과 접선 점을 방정식으로 대체하는 것입니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1622c6ecd4d43bb4fc4901b437464652_l3.png)
따라서 접선 방정식은 다음과 같습니다.
![]()
연습 2
곡선에 대한 접선의 방정식을 계산합니다.
![]()
좌표의 원점에서.
좌표의 원점은 점을 의미합니다.
![]()
그러므로 우리는 점에서 함수에 대한 접선을 계산해야 합니다.
![]()
먼저 좌표 원점에서 도함수를 계산하여 접선의 기울기 값을 결정합니다.
![]()
![]()
![]()
이 경우 우리는 접선이 통과하는 지점을 이미 알고 있습니다. 이 명령문은 선이 좌표의 원점, 즉 점에서 곡선에 접해야 함을 알려주기 때문입니다.
![]()
그래서 곡선과 접선이 공유하는 점이 점이다.
![]()
마지막으로, 기울기와 접선점에 대해 찾은 값을 방정식에 대입하면 됩니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)](https://mathority.org/wp-content/ql-cache/quicklatex.com-de8e4e9dbb7a5bca1d591612abcf7730_l3.png)
결론적으로 탄젠트 방정식은 다음과 같습니다.
![]()
![]()
연습 3
곡선의 접선을 계산합니다.
![]()
오른쪽과 평행한 곳
![]()
.
이 문제에서 우리는 접선이 선과 평행해야 한다고 들었습니다.
![]()
그리고 두 직선의 기울기가 같으면 평행합니다. 따라서 접선은 선과 동일한 기울기를 가져야 합니다.
![]()
즉, 선의 기울기를 찾아야 합니다.
![]()
이를 위해 변수를 지우고 다음을 수행합니다.
![]()
그래서 선의 기울기는
![]()
선의 기울기는 y가 깨끗할 때 x에 곱하는 숫자이므로 4입니다.
따라서 접선의 기울기도 4가 되어야 합니다. 왜냐하면 두 접선이 평행하려면 기울기가 같아야 하기 때문입니다.
![]()
이 경우 곡선과 접선 사이의 접선 지점을 알려주지 않습니다. 그러나 우리는 접선 지점에서 곡선의 도함수가 접선의 기울기와 같다는 것을 알고 있습니다. 즉
![]()
. 그렇다면 우리는 그 가치를 어떻게 알 수 있습니까?
![]()
, 우리는 방정식에서 x 0을 찾을 수 있습니다
![]()
이를 위해 먼저 다음의 미분값을 계산합니다.
![]()
![]()
이제 우리는 해결합니다
![]()
그것을 아는 것은
![]()
![]()
![]()
![]()
![]()
![]()
![]()
그리고 점의 x 좌표를 알면 다음을 계산하여 점의 다른 좌표를 찾을 수 있습니다.
![]()
![]()
따라서 곡선과 접선이 모두 통과하는 점이 점입니다.
![]()
남은 것은 발견된 기울기 값과 접선 점을 방정식으로 대체하는 것입니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f1f49e9bef505c5c71cffd15f0d29d0_l3.png)
그리고 탄젠트의 방정식은 다음과 같습니다.
![]()
연습 4
곡선의 접선을 계산합니다.
![]()
X축과 45°의 각도를 형성합니다.
문제 설명은 접선이 X축과 45°의 각도를 형성해야 함을 알려줍니다. 이러한 경우 기울기 값을 찾으려면 다음 공식을 적용해야 합니다.
![]()
![]()
명령문은 곡선과 접선 사이의 접선 지점을 지정하지 않습니다. 그러나 우리는 접선 지점에서 곡선의 미분이 접선의 기울기와 동일하다는 것을 알고 있습니다. 즉
![]()
. 따라서 다음 방정식을 풀어 x 0 을 계산할 수 있습니다.
![]()
이를 위해 먼저 다음의 미분값을 계산합니다.
![]()
![]()
이제 우리는 해결합니다
![]()
그것을 아는 것은
![]()
![]()
![]()
![]()
![]()
![]()
![]()
그리고 점의 x 좌표를 알면 다음을 계산하여 점의 다른 좌표를 찾을 수 있습니다.
![]()
![]()
따라서 곡선과 접선이 모두 통과하는 점이 점입니다.
![]()
남은 것은 발견된 기울기 값과 접선 점을 방정식으로 대체하는 것입니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=1 \qquad P(-1,-2) \end{array} \right\} \longrightarrow \ y -(-2)= 1(x-(-1))](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ed772b3993de50c4c67631a6fd33040_l3.png)
마지막으로 탄젠트 방정식을 찾기 위한 작업을 수행합니다.
![]()
![]()
![]()