이 글에서는 역(또는 역) 함수가 무엇인지, 그리고 함수의 역함수를 계산하는 방법을 설명합니다. 또한 함수에 역수가 있는지 여부와 이러한 유형의 함수의 속성을 쉽게 아는 방법도 알아봅니다. 마지막으로 역함수에 대한 단계별 연습을 통해 연습할 수 있습니다.
역함수는 무엇입니까?
역함수(reciprocal function)라고도 불리는 역함수는 정의역이 다른 함수(원래 함수)의 범위이고 범위가 원래 함수의 정의역인 함수입니다. 함수 f 의 역함수는 f -1 기호로 표현됩니다.
따라서 f(x) 의 역함수는 다음 조건을 만족하는 함수입니다.
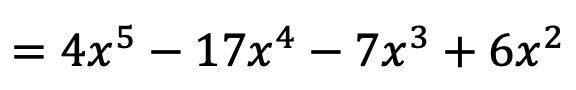
금
![]()
의 역함수이다
![]()
역함수의 개념은 함수 합성을 사용하여 정의할 수도 있습니다. 역함수로 구성된 모든 함수는 항등 함수와 동일하기 때문입니다.
![]()
➤ 참고: 함수 구성이란 무엇입니까?
따라서 이전 방정식이 충족되면 다음을 의미합니다.
![]()
는 의 역함수(또는 역함수)입니다.
![]()
역함수의 예
역함수의 정의가 주어지면 그 의미를 더 잘 이해하기 위해 예를 풀어보겠습니다.
- 다음 함수가 서로 역인지 확인합니다.
![]()
두 함수가 서로 반대인 경우 다음 두 가지 조건이 충족됩니다.
![]()
그럼 두 방정식이 모두 만족되는지 확인해 보겠습니다. 우리는 먼저 확인합니다
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7d5f4d815a58f808114ae471c31dd_l3.png)
➤ 방금 계산한 내용이 이해가 안 되시면 위 링크로 가서 함수 구성이 어떻게 되나요? , 이러한 유형의 작업을 함수로 해결하는 방법을 설명합니다.
하도록 하다
![]()
네, 이루어졌습니다. ✅
이제 평등을 확인해 봅시다
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83423fe7deab472f1a7e9575ec7af8c4_l3.png)
그리고 가역성 조건
![]()
그것은 또한 성취된다. ✅
결론적으로 두 방정식이 모두 성립하므로 두 함수는 서로 역입니다.
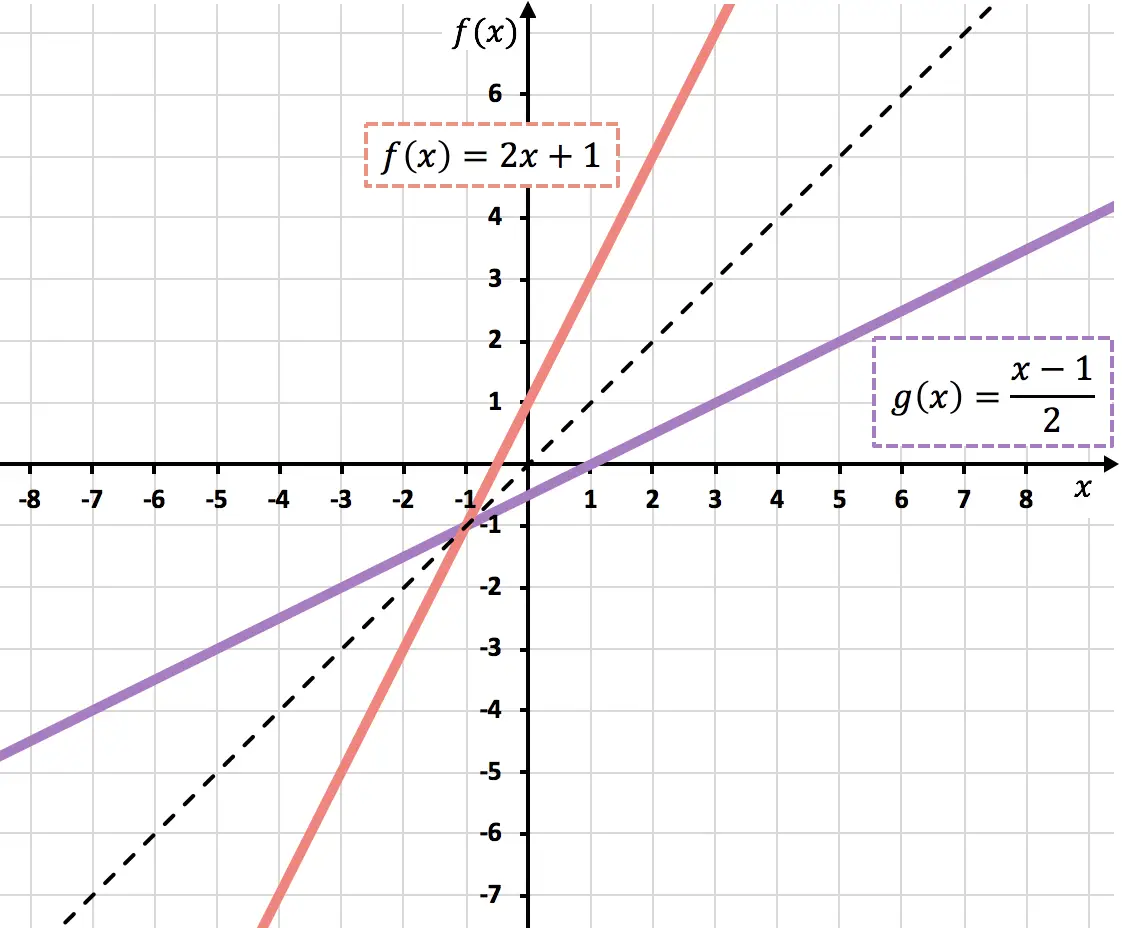
아래에서 두 함수를 모두 그래프로 볼 수 있습니다. 두 역함수의 그래프는 첫 번째와 세 번째 사분면의 이등분선에 대해 대칭입니다 .
함수에 역함수가 있는지 확인하는 방법
함수가 단사 함수인 경우, 즉 전체 영역의 각 값이 해당 간격의 단일 값에 해당하는 경우 함수는 역함수를 갖습니다 .
역함수를 갖는 지수 함수

역함수가 없는 이차 함수

예를 들어, 왼쪽 지수 함수는 각 x가 f(x) 의 단일 값에 대응하기 때문에 역함수를 가집니다. 반면, 오른쪽 이차 함수는 이미지가 동일한 여러 x 값을 갖기 때문에 역함수를 갖지 않습니다(예: f(1)=f(3)=2) .
마찬가지로, 전단사 함수는 단사 및 전사 함수로 구성되므로 모든 전단사 함수에는 역함수도 있습니다.
반면에, 역함수는 함수의 곱셈의 역원 과 동일한 것이 아니라 두 가지 다른 개념이라는 점을 명심해야 합니다. 함수의 곱셈의 역함수를 찾으려면 해당 함수에 대한 1개의 대응 관계를 계산하면 됩니다.
![]()
다음 섹션에서는 역함수를 결정하는 방법을 살펴보겠습니다.
역함수를 찾는 방법
함수의 역함수를 계산하려면 다음 단계를 수행해야 합니다.
- f(x)를 y 로 바꿉니다.
- 모든 x를 y 로 변경하고 그 반대로 변경합니다.
- y 변수를 지웁니다.
- 변수 y를 f -1 (x) 로 바꿉니다. 역함수는 f -1 (x) 에 대해 구한 표현식입니다.
역함수가 어떻게 계산되는지 정확히 볼 수 있도록 다음 함수의 역함수를 예로 들어 보겠습니다.
![]()
우선 교체를 해야 합니다
![]()
을 위한
![]()
:
![]()
이제 우리는 모든 것을 바꾼다
![]()
기능의
![]()
, 그 반대:
![]()
그런 다음 변수를 지웁니다.
![]()
![]()
![]()
![]()
![]()
그리고 마지막으로, 역함수
![]()
는 우리가 분리하여 얻은 대수적 표현입니다.
![]()
![]()
역함수의 해결 연습
아래에서는 여러분이 연습할 수 있도록 역함수에 대한 몇 가지 단계별 연습을 준비했습니다.
👉 연습 문제 해결 방법을 이해하지 못하거나 문제 해결을 원하시면 댓글로 글을 남겨주세요!
연습 1
다음 두 함수가 역(또는 역)인지 여부를 확인하세요.
![]()
두 함수가 서로 역이 되려면 다음이 참이어야 합니다.
![]()
따라서 두 가지 조건이 충족되는지 확인하는 것이 필요합니다. 우리는 먼저 확인합니다
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbbdf5bb2c308a1973c5f2d99e822ad5_l3.png)
아직,
![]()
네, 이루어졌습니다. ✅
이제 다른 기능 구성을 확인해 보겠습니다.
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5819584c8358b812c8214a902e4f08_l3.png)
이로써
![]()
그것은 또한 성취된다. ✅
어떻게 그런 일이 일어나나요?
![]()
그리고
![]()
, 두 함수는 서로 반대입니다.
연습 2
다음 1차 다항식 함수의 역함수(또는 역함수)를 계산합니다.
![]()
함수를 역전시키기 위해 가장 먼저 해야 할 일은 용어를 대체하는 것입니다.
![]()
을 위한
![]()
![]()
이제 우리는
![]()
~에 의해
![]()
, 그 반대:
![]()
그런 다음 출시합니다.
![]()
![]()
![]()
![]()
![]()
이미 출시에 성공했어요
![]()
. 그러므로, 의 역함수는
![]()
동쪽:
![]()
연습 3
다음 2차 다항식 함수를 반전시킵니다.
![]()
역함수를 찾기 위해 위에서 본 절차를 따릅니다. 그래서 우리는 전화할 것이다
![]()
기능에
![]()
![]()
둘째, 우리는
![]()
에 대한
![]()
, 그 반대:
![]()
그리고 마지막으로 변수를 분리합니다.
![]()
![]()
![]()
![]()
![]()
그러나 이 경우 얻은 함수는 해당 도메인의 각 요소에 대해 두 개의 이미지(양수 이미지와 음수 이미지)를 갖습니다. 따라서 문제 함수의 역함수는 존재하지 않습니다 .
연습 4
다음 유리 함수의 역함수(또는 역함수)를 결정합니다.
![]()
먼저 교체해보겠습니다
![]()
을 위한
![]()
![]()
이제 우리는
![]()
분자와 분모
![]()
, 그 반대:
![]()
그런 다음 출시합니다.
![]()
![]()
표현식
![]()
는 방정식의 오른쪽 전체를 나누므로 방정식의 왼쪽 전체를 곱하여 곱할 수 있습니다.
![]()
![]()
우리는 모든 용어를 다음과 같이 설정합니다.
![]()
방정식의 한쪽에는 다른 항이 있고 다른 쪽에는 다음과 같은 항이 있습니다.
![]()
클리어하기 위해서는
![]()
, 방정식의 왼쪽에서 공통 인수를 추출합니다.
![]()
그리고 우체부로서
![]()
방정식의 왼쪽 전체를 곱하는 것입니다. 오른쪽 전체를 나누어 이를 수행할 수 있습니다.
![]()
이미 출시에 성공했어요
![]()
. 따라서 역함수는
![]()
동쪽:
![]()
역함수의 속성
역함수에는 다음과 같은 특징이 있습니다.
- 역함수는 고유합니다. 즉, 함수가 가역인 경우 이 함수에는 단 하나의 역함수가 있습니다.
- 역함수의 정의역은 원래 함수의 범위(또는 범위)입니다.
- 마찬가지로 역함수의 경로는 원래 함수의 정의역과 동일합니다.
- 역함수로 구성된 모든 함수는 항등함수(x)를 제공합니다.
![]()
- 함수 그래프와 역함수 그래프는 제1사분면과 제3사분면의 이등분선을 기준으로 대칭입니다.
- 역함수의 역함수는 원래 함수와 같습니다.
![]()
- 복합 함수를 반전시키는 것은 각 함수의 역함수를 개별적으로 계산한 다음 역함수를 합성하는 것과 같습니다.
![]()
- 함수는 역함수와 동시에 연속입니다. 즉, 함수가 연속이면 역함수도 마찬가지입니다.
- 함수가 미분 가능하고 도함수는 언제든지 사라지지 않는 경우
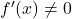
, 그 역함수도 미분 가능합니다.
또한 역함수의 미분은 역함수 정리를 적용하여 계산할 수 있으며 그 공식은 다음과 같습니다.
![]()