이 페이지에서는 숫자의 다항식 분해(또는 표현)를 수행하는 방법을 설명합니다. 여기서는 다항식 분해의 예를 볼 수 있으며, 또한 연습할 수 있는 단계별 연습 문제도 찾을 수 있습니다.
숫자의 다항식 분해란 무엇입니까?
수학에서 숫자의 다항식 분해는 해당 숫자를 합계로 표현하는 것으로 구성되며, 합계의 각 항은 숫자의 각 자릿수를 10진수로 곱한 것입니다.
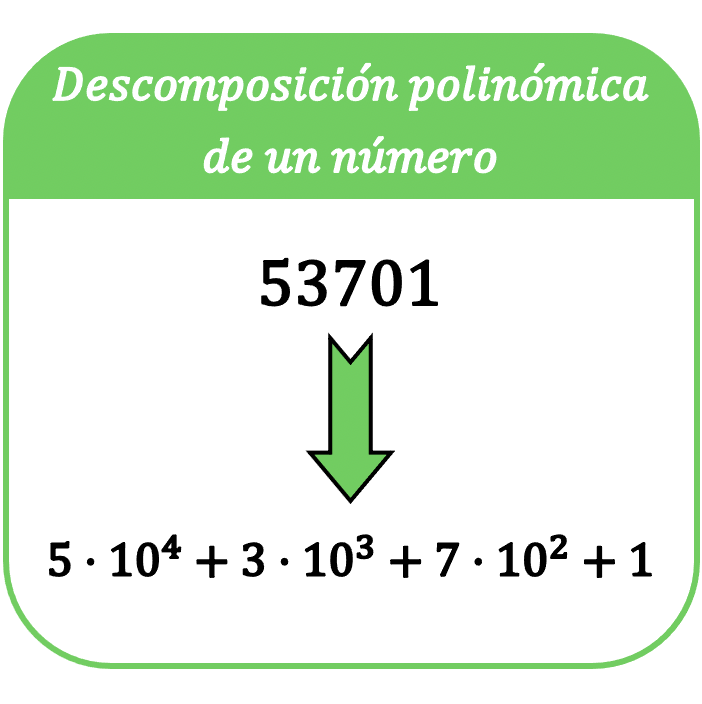
숫자의 다항식 분해라는 용어는 숫자의 다항식 표현 으로도 알려져 있습니다.
다항식 분해를 수행하는 방법
숫자의 다항식 분해를 수행하려면 숫자의 각 자릿수 에 오른쪽 자릿수만큼 10을 곱해야 합니다.
예를 들어, 다음 숫자의 다항식 분해를 계산하려는 경우:
![]()
이 경우 숫자 8은 5번째 자리를 차지하므로 오른쪽에 4자리가 있습니다. 그러므로 우리는 8을 10의 4제곱으로 곱해야 합니다.
![]()
따라서 숫자 86293을 다항식 분해하려면 숫자의 모든 자릿수에 대해 동일한 작업을 수행하고 모든 곱셈을 합계 형식으로 표현해야 합니다.
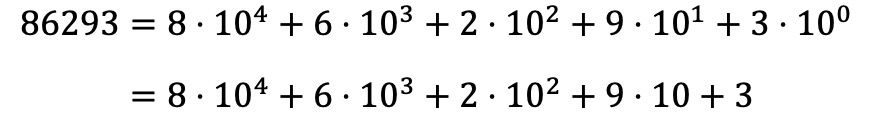
거듭제곱의 특성에 따라 0 으로 올림된 모든 숫자는 1과 같으므로 10 0 =1이기 때문에 10 0 거듭제곱은 사라집니다.
반면에 곱셈 분해를 통해 숫자의 다항식 분해를 찾을 수도 있습니다.
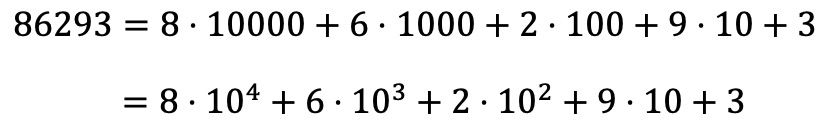
숫자의 다항식 분해의 예
숫자의 다항식 분해가 어떻게 수행되는지 살펴본 후에는 개념을 완전히 이해하기 위해 이러한 유형의 연산에 대한 다양한 예를 볼 것입니다.
- 3641의 다항식 분해:
![]()
- 56912의 다항식 분해:
![]()
- 27084의 다항식 분해:
![Rendered by QuickLaTeX.com \begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f72230330ff9c9150dc9ab19a89a42d8_l3.png)
이 마지막 예에서는 0을 곱한 숫자가 상쇄되므로 세 번째 곱셈을 단순화할 수 있습니다.
십진수의 다항식 분해
우리는 방금 자연수의 다항식 분해를 수행하는 방법을 살펴보았습니다. 그런데… 십진수를 다항식으로 어떻게 분해합니까?
음, 십진수 를 사용한 다항식 분해는 정수와 동일한 방식으로 수행되지만, 추가적으로 우리는 각 십진수의 곱에 밑수 10의 거듭제곱을 곱한 값을 더합니다. 지수는 해당 숫자가 차지하는 소수 위치를 음수로 나타냅니다. 징후.
말로 설명하면 매우 복잡해 보일 수 있지만, 예를 들어 보면 이해가 더 잘 된다는 것을 알 수 있습니다.
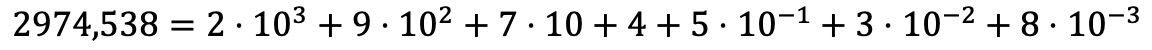
다항식 분해 연습 해결
다항식 분해를 연습할 수 있도록 단계별로 해결되는 몇 가지 연습 문제를 준비했습니다.
궁금한 점은 댓글로 남겨주세요! 🤔🤔🤔
연습 1
다음 숫자의 다항식 분해를 수행합니다.
![]()
![]()
![]()
![]()
숫자의 다항식 분해를 찾으려면 해당 숫자의 각 자릿수에 10을 오른쪽 자릿수만큼 곱한 다음 모든 곱셈을 더합니다. 아직:
![]()
![]()
![]()
![]()
연습 2
다음 숫자의 다항식 분해를 구합니다.
![]()
![]()
![]()
![]()
숫자를 다항식으로 분해하려면 해당 숫자의 각 자릿수에 10을 오른쪽 자릿수만큼 곱한 다음 모든 곱을 더해야 합니다. 아직:
![]()
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e3500d6a94685566b267e8708e8b0d7_l3.png)
![]()
![]()
연습 3
다음 소수의 다항식 분해를 계산합니다.
![]()
![]()
![]()
![]()
이 문제에서 모든 숫자는 소수이므로 분해하려면 소수가 아닌 각 숫자에 소수점까지의 자릿수만큼 10을 곱하고 각 소수점 이하 자릿수에 소수점 이하 자릿수까지 10을 곱해야 합니다. 부정적인 신호.
![]()
![]()
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-deb6b85265df2e98bcb5e116e19c397f_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e204c24ba4f9138f503cf2c2a0e379d_l3.png)