이 페이지에서는 세 벡터의 혼합 곱(또는 삼중 도트 곱)이 무엇인지, 그리고 계산 방법을 설명합니다. 또한 이러한 유형의 벡터 간의 연산에 대한 예제, 연습 및 해결된 문제도 볼 수 있습니다. 그리고, 혼합제품의 특성과 활용도를 확인하실 수 있습니다.
세 벡터의 혼합곱은 무엇인가?
삼중 내적 이라고도 하는 세 벡터의 혼합 곱은 두 가지 다른 유형의 연산, 즉 내적 과 벡터 곱을 포함하는 세 벡터 간의 연속적인 곱셈입니다. 따라서 두 벡터 연산의 조합은 스칼라(실수)를 제공합니다.
구체적으로, 혼합 곱은 두 벡터의 벡터 곱을 계산한 후 세 번째 벡터에서 얻은 결과를 벡터적으로 곱하는 것으로 구성됩니다. 이렇게 작성하면 매우 복잡해 보일 수 있지만 실제로는 그렇게 많지 않습니다. 삼중점 곱의 공식을 살펴보세요.
![]()
공식에서 볼 수 있듯이 세 벡터의 혼합 곱은 두 개의 대괄호로 표시됩니다.
세 벡터의 혼합 곱을 계산하는 방법은 무엇입니까?
삼중 내적 공식은 이전 섹션에서 본 공식이지만, 더 간단하고 빠른 또 다른 방법이 있기 때문에 일반적으로 세 벡터의 혼합 곱을 결정하는 데 사용되지 않습니다.
임의의 3개 벡터를 다음과 같이 설정합니다.
![]()
세 벡터 사이의 혼합 곱을 계산하려면 벡터의 구성요소로 형성된 3×3 행렬식을 간단히 풀면 됩니다.
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fed933d4d02bb5ca6f5bae06ea544d_l3.png)
따라서 이것이 어떻게 계산되는지에 대한 예를 볼 수 있으며 다음 세 벡터의 혼합 곱을 찾을 수 있습니다.
![]()
혼합 곱을 결정하기 위해 행렬의 행에 벡터를 배치하여 3차 행렬식을 구성합니다.
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5341b4a39b42c1284a4b0129b38b61a_l3.png)
이제 우리는 행렬식을 풀기만 하면 됩니다. 이를 위해서는 어떤 방법이든 사용할 수 있습니다. 이 경우 Sarrus의 규칙을 적용합니다(그러나 이는 덧셈이나 보조 인자로도 수행할 수 있습니다).
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df86565048cf897265878936f2294525_l3.png)
두 절차가 동일하다는 것을 보여주기 위해 정의를 통해 동일한 벡터의 혼합 곱을 계산합니다.
![Rendered by QuickLaTeX.com \begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4d15d610ca9b4cb39e9f268cfb152ae_l3.png)
벡터의 행렬식을 통해 혼합 곱을 계산하는 것이 더 빠르고 실수할 가능성이 적기 때문에 권장됩니다. 하지만 보시다시피 어떤 방법을 사용해도 결과는 동일하므로 선호하는 방법을 사용하세요. 👍
혼합제품의 기하학적 해석
세 벡터의 혼합 곱을 찾는 방법을 알게 되면 궁금할 것입니다. 혼합 곱의 용도는 무엇입니까? 음, 수학에서는 두 가지 주요 용도가 있습니다. 평행육면체의 부피를 계산하는 것과 사면체의 부피를 계산하는 것입니다.
평행육면체의 부피는 기하학적 장의 3차원을 표시하는 벡터의 혼합 곱의 절대값과 같습니다.
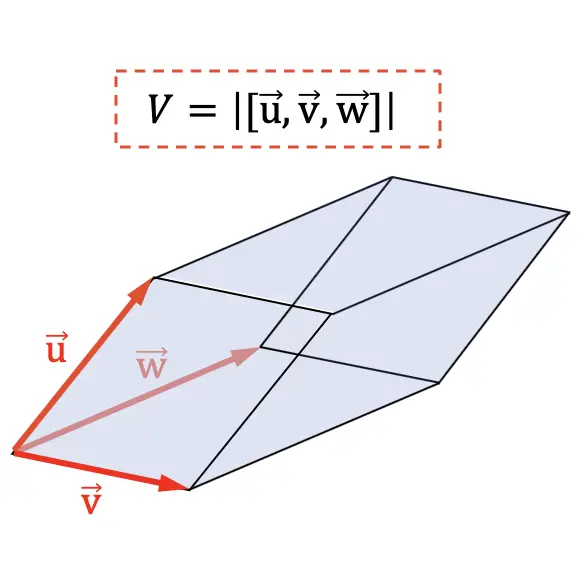
혼합 생성물의 또 다른 응용은 사면체의 부피를 결정하는 것입니다. 기하학적으로 혼합 생성물의 절대값의 6번째 부분은 사면체의 부피를 나타내기 때문에:
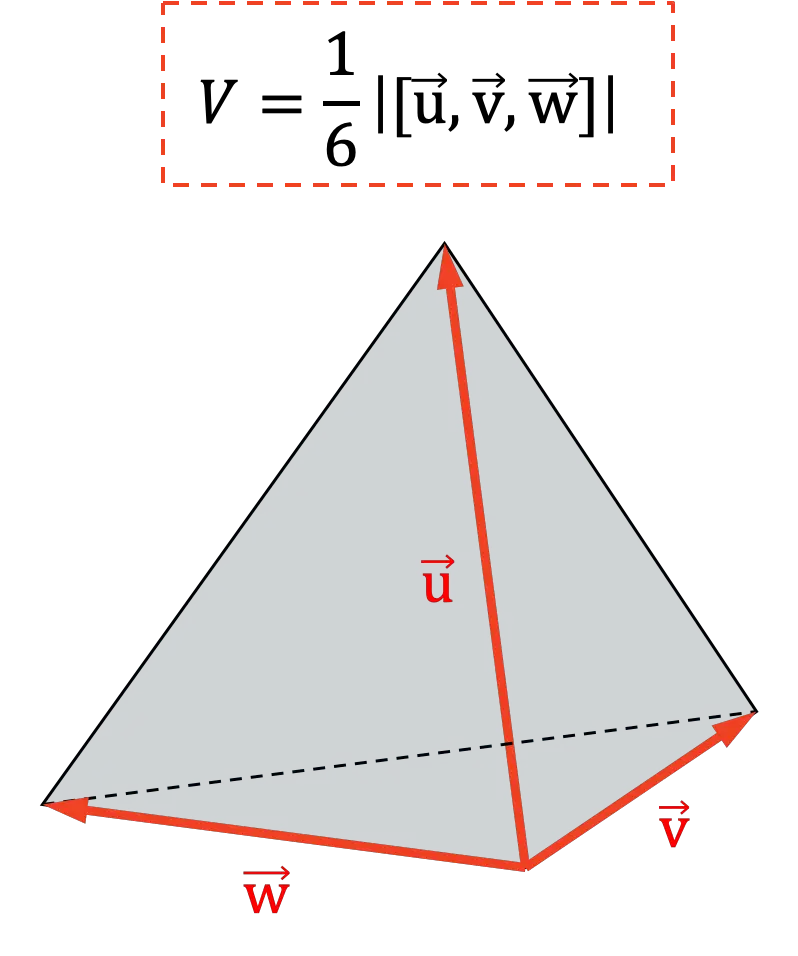
혼합제품 또는 삼중점 제품의 특성
혼합 제품 또는 삼중 스칼라 제품은 다음과 같은 특성을 갖습니다.
- 일반적으로 혼합곱 벡터의 순서 가 바뀌면 부호도 바뀌게 된다. 따라서 혼합된 제품 벡터의 순서가 중요합니다.
![]()
- 그러나 순서를 주기적으로 변경하면 부호는 변경되지 않습니다.
![]()
- 3차원 공간(R3)에서 3개의 선형 종속 또는 동일 평면 벡터(동일한 평면에 속함)의 혼합 곱은 0과 같습니다.
혼합 제품 문제 해결
연습 1
3개의 벡터가 주어지면:
![]()
세 벡터의 혼합 곱을 계산합니다.
![]()
혼합 곱을 찾으려면 벡터의 좌표로 구성된 행렬식을 풀어야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-549ed90889d541ae4a1075449567b062_l3.png)
연습 2
3개의 벡터가 주어지면:
![]()
세 벡터 사이의 혼합 곱을 결정합니다.
![]()
혼합 곱을 찾으려면 선 형태의 벡터의 데카르트 좌표를 갖는 행렬식을 풀어야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29b46155243552a99f6fd75de69f59da_l3.png)
연습 3
세 변이 다음 벡터인 평행육면체의 부피를 계산하세요.
![]()
평행육면체의 부피는 모서리로 갖는 3개의 벡터를 혼합한 곱의 절대값과 같습니다. 따라서 먼저 벡터의 삼중 교차 곱을 계산합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9718b369a508216fbb69ab68ac7de381_l3.png)
따라서 평행 육면체의 부피는 혼합 제품 결과의 절대 값입니다.
![]()
연습 4
정점이 다음 점인 사면체의 부피를 계산하십시오.
![]()
먼저, 사면체의 모서리를 나타내는 벡터를 계산합니다.
![]()
![]()
![]()
사면체의 부피는 모서리에 대해 갖는 벡터 3개의 혼합 곱 절대값의 6분의 1에 해당합니다. 따라서 먼저 발견된 벡터의 혼합 곱을 계산합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d384e76415a756b834e0a8e7c695b1c1_l3.png)
따라서 사면체의 부피는 혼합된 제품의 절대값의 1/6이 됩니다.
![]()