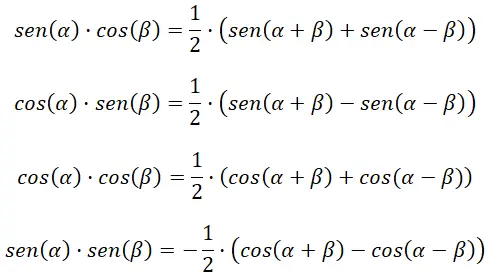삼각법 항등식은 서로 다른 삼각 함수 간의 동일성입니다. 이러한 삼각법 등가성 덕분에 우리는 다른 삼각법 비율을 기반으로 특정 삼각법 비율을 추론할 수 있습니다. 따라서 삼각함수 공식을 이해하려면 이러한 비율의 공식을 알아야 합니다. 귀하의 경우에 해당 내용을 모르신다면 마지막 링크를 방문하시는 것이 좋습니다.
삼각법 항등식 표
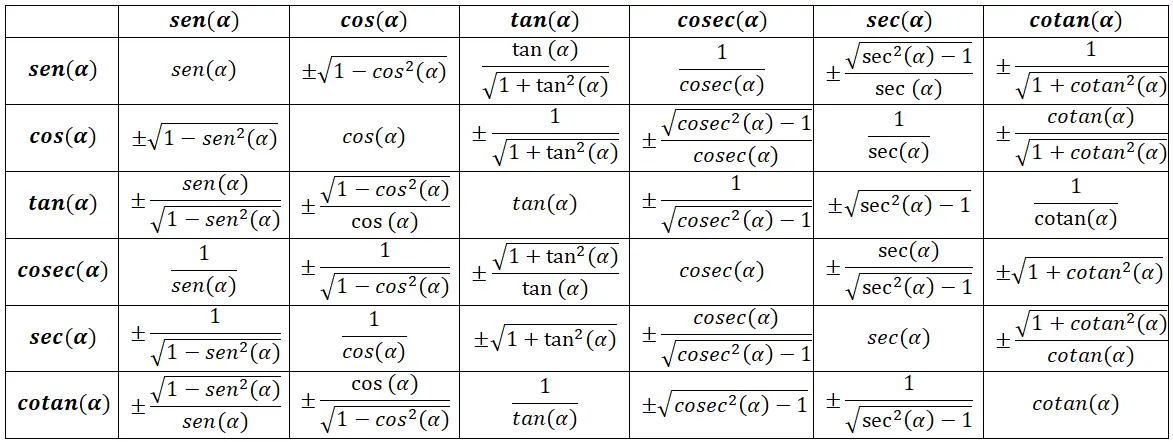
기본 삼각 항등식
다른 것들에 대한 이론적 기초를 제공하기 때문에 가장 중요하다고 간주되는 일련의 기본 삼각법 항등식이 있습니다. 이는 가장 쉽게 찾을 수 있고 아마도 가장 직관적이기 때문에 기억하기 가장 쉬울 것입니다. 모든 수식은 다음 이미지를 기반으로 한다는 점을 기억하세요.

기본 삼각 항등식
모든 것의 첫 번째 항등식은 사인과 코사인의 관계라고도 알려진 기본 삼각 항등식 입니다. 다음은 수학적 증명입니다: sin²(α) + cos²(α) = 1.
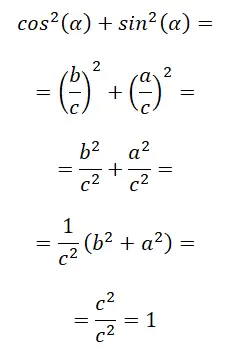
마지막 단계에서는 기본적으로 피타고라스 정리를 적용합니다. c² = a² + b²이므로 c² / c²는 1과 같습니다. 결론적으로 다음과 같이 말할 수 있습니다. sin² (α) + cos² (α) = 1.
시컨트와 탄젠트의 관계(시컨트 제곱)
둘째, 우리는 시컨트와 탄젠트를 연결하는 삼각법적 항등식을 가지며, 그 표현은 다음과 같습니다: sec² (α) = 1 + tan² (α) . 다음 이미지에서는 이 ID를 구성하는 몇 가지 미리 알림 공식과 최종 공식에 도달하기 위해 따라야 할 절차를 볼 수 있습니다.
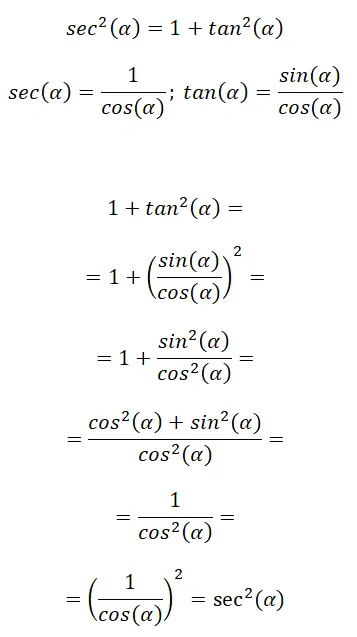
이 경우 삼각비 공식을 사용하여 다른 비율을 찾습니다. 결론적으로, sec²(α) = 1 + tan²(α)라고 말할 수 있습니다.
코시컨트와 코탄젠트의 관계(코시컨트 제곱)
코시컨트와 코탄젠트의 정의로부터 우리는 탄젠트 공식에서 연결점을 찾을 수 있습니다. 덕분에 우리는 또 다른 삼각법적 항등식인 cosec² (α) = 1 + cotg² (α) 을 추론할 수 있습니다.
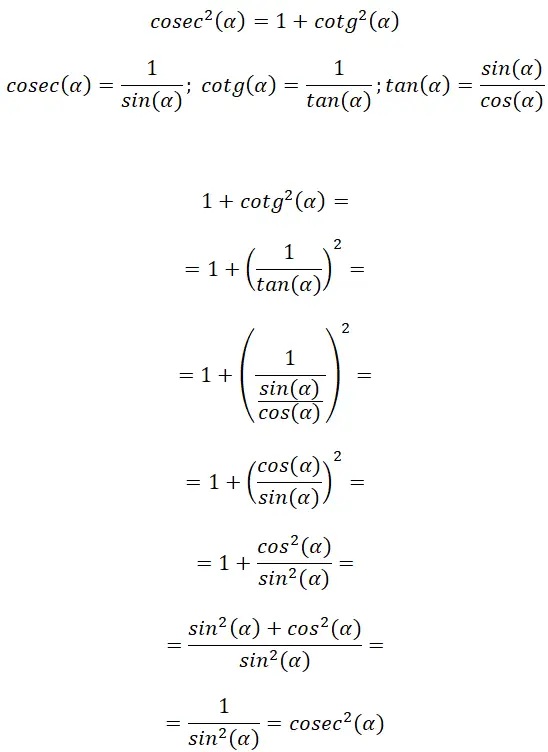
이 데모를 통해 cosec²(α) = 1 + cotg²(α)를 확인할 수 있습니다. 또한 탄젠트와 코탄젠트의 유사성으로 인해 이 관계가 이전 관계와 어느 정도 유사하다는 것을 알 수 있습니다.
합각과 뺄셈각의 삼각비
각도 합 또는 각도 빼기 비율은 두 각도의 덧셈 또는 뺄셈의 삼각비를 계산하여 얻은 일종의 항등식입니다. 예를 들어, 90 + 60의 사인을 계산하려는 경우 이 계산을 더 쉽게 해주는 일련의 공식이 있습니다. 다음은 이 스타일의 삼각법 항등식에 대한 모든 공식이 포함된 목록입니다.
각도 합의 사인: sin (α + β ) = sin (α) cos ( β ) + cos ( α ) sin ( β )
각도 빼기의 사인: sin (α – β ) = sin (α) cos ( β ) – cos ( α ) sin ( β )
각도 합의 코사인: cos (α + β ) = cos (α) cos ( β ) – sin ( α ) sin ( β )
각도코사인 빼기: cos (α – β ) = cos (α) cos ( β ) + sin ( α ) sin ( β )
각도 합의 탄젠트: tan (α + β ) = (tan (α) + tan ( β )) ¼ (1 – tan (α) tan ( β ))
각탄젠트 빼기: tan(α – β ) = (tan(α) + tan( β )) ¼(1 + tan(α)tan( β ))
150°의 사인을 계산하는 것이 (90° + 60°)의 사인을 계산하기 위해 방금 설명한 공식을 사용하는 것보다 쉽다는 것은 분명합니다. 그러면 이 공식이 왜 중요한가요? 대답은 이러한 항등식을 통해 간단한 각도에서 복잡한 각도 의 삼각비를 계산할 수 있다는 것입니다. 따라서 주목할만한(가장 관련성이 높은) 각도의 비율을 기억하면 150°와 같은 더 복잡한 각도의 비율을 계산하기 위해 계산기를 사용할 필요가 없습니다.
이중 각도 삼각비
이중 각(2α)의 삼각비를 계산하려면 일련의 항등식을 사용하여 계산할 수 있습니다. 보다 정확하게는 이전 섹션에서 논의한 것과 매우 유사한 공식을 통해 이를 수행할 수 있습니다. β를 α로 바꾸면 이전 표현식에서는 (α + α)가 남고 이는 (2α)와 같습니다. 이를 염두에 두고 다음과 같은 정체성을 도출할 수 있습니다.
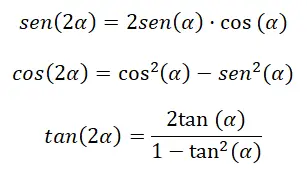
아래에서 데모를 볼 수 있습니다.
이중 각도의 사인: sin(2α) = sin(α) cos(α) + cos(α) sin(α) = 2 sin(α) cos(α)
이중 각도의 코사인: cos (α + α ) = cos (α) cos ( α ) – sin ( α ) sin ( α ) = cos² (α) – sin² (α)
이중 접선 각도: tan(2α) = 2 tan(α) ¼(1 – tan²(α))
반각의 삼각비
또한 반각(α/2)의 삼각비를 계산할 수 있는 항등식도 있습니다.
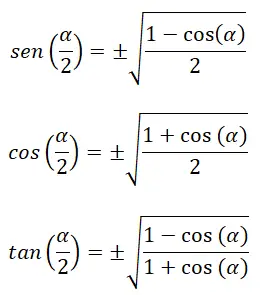
다음과 같은 이미 알려진 공식 중:
1 = sin²( β ) + cos²( β )
cos( 2β ) = cos²( β ) – sin²( β )
β = α/2로 만들면 사인의 경우 두 표현식을 빼고 코사인의 경우 이를 더한 다음 얻은 두 공식(사인의 공식과 코사인의 공식)을 나눔으로써 이러한 항등식을 증명할 수 있습니다. 탄젠트의 경우. 그러나 아래에서 얻은 공식에서 계산하려는 비율을 분리하는 것이 남아 있습니다.
반사인각: 1 – cos(α) = 2 sin²(α/2); sin² (α/2) = (1 – cos (α)) ¼ 2
반각 코사인: 1 + cos(α) = 2 cos²(α/2); cos²(α/2) = (1 + cos(α)) ¼ 2
삼중각의 삼각비
삼중각(3α)이 있는 경우 특정 항등식을 사용하여 삼각비를 계산할 수도 있습니다. 이러한 항등식은 이미 설명된 이중 각도 항등식, 합 각도 항등식 및 삼각법의 기본 항등식에서 비롯됩니다.
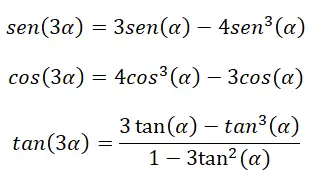
이러한 항등식을 증명하려면 각도 합 공식을 사용해야 합니다.
각도 합의 사인: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α)
각도 합의 코사인: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α)
그래서 방금 이야기한 식에 있는 이중각의 공식을 적용하고 삼각법의 기본 항등식을 적용하면 항등식을 증명할 수 있습니다. 기본적인 삼각법 항등식을 사용하면 표현식의 모든 비율을 하나로 변환할 수 있다는 점은 언급할 가치가 있습니다. 삼중각의 사인 공식은 사인만으로 구성되고, 코사인 공식은 코사인만으로 구성되는 이유가 여기에 있습니다. 아래에서 전체 절차를 볼 수 있습니다.
삼중각의 사인: sin (3α) = sin (α + 2α) = sin (α) cos (2α) + sin (2α) cos (α) =
= sin (α) (cos² (α) – sin² (α)) + 2 sin (α) cos (α) cos (α) =
= 죄(α) cos²(α) – sin³(α) + 2 죄(α) cos²(α) =
= sin (α) · (1 – sin² (α)) – sin³ (α) + 2 sin (α) · (1 – sin² (α)) =
= 죄(α) – 죄3(α) – 죄3(α) + 2 죄(α) – 2 죄3(α) =
= 3 죄(α) – 4 죄3(α)
삼중각의 코사인: cos (3α) = cos (α + 2α) = cos (α) cos (2α) – sin (α) sin (2α) =
= cos(α) (cos²(α) – sin²(α)) – sin(α) 2 sin(α) cos(α) =
= cos³ (α) – cos (α) sin² (α) – 2 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) sin² (α) =
= cos³ (α) – 3 cos (α) · (1 – cos² (α)) =
= cos²(α) – 3cos²(α) + 3cos²(α) =
= 4 cos³(α) – 3 cos(α)
마지막으로, 삼중각의 탄젠트는 두 가지 방법으로 계산할 수 있습니다. 첫 번째는 사인 공식을 코사인 공식으로 나누는 것이고, 두 번째는 이중각의 탄젠트에 대한 표현식을 다음 공식에 대입하여 각도 합: tan (α + 2α) = (tan (α) + tan (2α)) ¼ (1 – tan (α) tan (2α)).
각도 종류에 따른 삼각함수 항등식
삼각비를 직접적이고 빠르게 계산할 수 있는 규칙이 되는 일련의 공식에 대해 언급하는 것이 중요합니다. 사실, 그것은 우리가 방금 이야기한 모든 표현과 동일한 특성을 충족시키기 때문에 삼각법 항등식으로 간주될 수도 있습니다. 더 정확하게 말하면, 이 공식을 통해 한 각도와 다른 각도의 관계로부터 각도의 삼각 관계를 결정할 수 있습니다.
보완 각도
보각 (α 및 β )은 합이 90°인 각도이므로 이를 더하면 직각이 됩니다. α가 β 의 보각임을 확인하려면 매우 간단한 방정식을 풀어야 합니다. α = 90 – β 이 등가의 결과가 일치하면 두 값이 상보적이라는 것을 확인할 수 있습니다. 이러한 동일성 덕분에 우리는 한 각도의 삼각비를 다른 각도의 삼각비로 추론할 수 있습니다.
보각의 사인: sin(90° – α) = cos(α)
보각의 코사인: cos(90° – α) = sin(α)
보각의 탄젠트: tan(90° – α) = cotan(α)
보각의 코시컨트: cosec(90° – α) = sec(α)
보각의 시컨트: sec(90° – α) = cosec(α)
보각의 코탄젠트: cotan(90° – α) = tan(α)
추가 각도
보각 (α 및 β )은 합이 180° 또는 π 라디안인 각도이므로 α + β = 180°라는 공식을 추론할 수 있습니다. 즉, α의 보각이 β 라면 다음의 β = 180 – α 식이 만족되어야 한다. 그러면 다음 각도에서 추론할 수 있는 신원 목록을 볼 수 있습니다.
보각의 사인: sin(180° – α) = sin(α)
추가 각도의 코사인: cos (180° – α) = -cos (α)
보각의 탄젠트: tan (180° – α) = -tan (α)
추가 각도의 코시컨트: cosec(180° – α) = cosec(α)
보각의 시컨트: sec(180° – α) = -sec(α)
보각의 코탄젠트: cotan (180° – α) = -cotan (α)
켤레 각도
켤레 각도 (α 및 β )는 합이 360° 또는 2π 라디안인 각도이므로 α + β = 360° 공식을 추론할 수 있습니다. 그리고 이 첫 번째 공식에서 각도 중 하나를 다른 각도로 표현하면 다음과 같습니다: α = 360° – β 또는 β = 360° – α. 이제 공액 각도의 평등을 보여 드리겠습니다.
켤레각의 사인: sin (360° – α) = – sin (α)
공액각의 코사인: cos (360° – α) = cos (α)
공액각의 탄젠트: tan (360° – α) = – tan (α)
켤레각의 코시컨트: cosec(360° – α) = – cosec(α)
공액각의 시컨트: 초(360° – α) = 초(α)
공액각의 코탄젠트: cotan (360° – α) = – cotan (α)
반대 각도
반대 각도 또는 음의 각도 (α 및 β )는 동일한 수치 값을 가지지만 부호가 다른 각도입니다. 이러한 유형의 각도의 예는 30° 및 -30°입니다. 음수 부호는 회전이 시계 방향임을 나타내고 양수 각도는 시계 반대 방향으로 회전한다는 것을 기억해야 합니다.
반대각의 사인: sin(-α) = – sin(α)
반대각의 코사인: cos(-α) = cos(α)
반대각의 탄젠트: tan (-α) = – tan (α)
반대각의 코시컨트: cosec(-α) = – cosec(α)
반대각의 시컨트: sec(-α) = sec(α)
반대각의 코탄젠트: cotan (-α) = – cotan (α)
90°와 다른 각도 또는 각도 플러스/마이너스 π/2
90°만큼 다른 각도 또는 각도 +/- π/2 (α 및 β )는 90° 차이가 있는 각도입니다. 따라서 β – α = 90°로 표현될 수 있습니다. 여기서 β 는 α 보다 90° 더 큽니다. 이 각도에는 두 각도의 삼각비를 연결하는 일련의 공식도 있습니다.
90°와 다른 각도의 사인: sin(90° + α) = cos(α)
90°와 다른 각도의 코사인: cos (90° + α) = -sin (α)
90°와 다른 각도의 접선: tan(90° + α) = – cotan(α)
90°와 다른 각도의 코시컨트: cosec(90° + α) = sec(α)
90°와 다른 각도의 시컨트: sec(90° + α) = -cosec(α)
90°와 다른 각도의 코탄젠트: cotan(90° + α) = -cotan(α)
180°와 다른 각도 또는 각도 플러스/마이너스 π
플러스/마이너스 각도 π (α 및 β )는 180° 차이가 나는 각도와 같습니다. 따라서 다음 공식을 사용하여 표현할 수 있습니다: β – α = 180°, 여기서 β 180°는 α 보다 큽니다. 다음으로, 이러한 각도의 삼각비와 관련된 삼각법적 항등식을 보여줍니다.
180°와 다른 각도의 사인: sin (180° + α ) = -sin ( α )
180°와 다른 각도의 코사인: cos (180° + α ) = -cos ( α )
180°와 다른 각도의 탄젠트: tan (180° + α ) = tan ( α )
180°와 다른 각도의 코시컨트: cosec (180° + α ) = -cosec ( α )
180°와 다른 각도의 시컨트: sec (180° + α ) = -sec ( α )
180°와 다른 각도의 코탄젠트: cotan (180° + α ) = cotan ( α )
삼각비의 변환
마지막으로, 다른 연산을 통해 특정 삼각비를 표현할 수 있는 삼각법 항등식이 있습니다. 따라서 비율의 합이 있고 이를 곱으로 표현하고 싶다면 다음 공식을 사용할 수 있습니다. 안타깝게도 모든 산술 연산에는 표현식이 없지만 덧셈과 뺄셈에서 곱으로 또는 그 반대로 만 갈 수 있습니다.
덧셈이나 뺄셈을 곱으로 변환
다음 네 가지 공식은 삼각 함수의 덧셈과 뺄셈을 계산하는 데 도움이 됩니다.
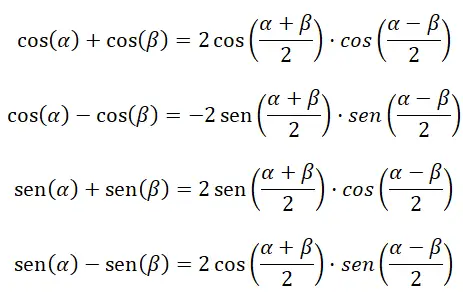
제품을 덧셈 또는 뺄셈으로 변환
다음 네 가지 공식은 삼각 함수의 곱을 계산하는 데 도움이 됩니다.