복리 란 단순히 이미 갖고 있는 돈에서 원래 원금에 더해 발생하는 이자를 말합니다. 간단해 보일 수도 있지만 복리를 효과적으로 계산하려면 고려해야 할 요소가 많이 있습니다. 이 기사에서 우리는 그것들을 모두 설명할 것입니다.
복리 계산기
복리 계산기를 사용하면 사용자는 투자에 대한 복리 이자를 계산할 수 있습니다. 예를 들어, 투자에 대한 이자를 계산하는 데 사용할 수 있습니다. 계산기는 사용하기 쉬우며 사용자가 초기 투자 금액, 연간 기부금, 이자율 및 기간을 입력해야 합니다.
그리고 이 데이터로부터 이 계산기는 투자로 인해 창출될 최종 금액을 결정할 수 있습니다.
복리란 무엇입니까?
복리란 원금에 이자가 붙은 이자율을 말합니다. 이는 단순이자와 는 상당히 다른 개념입니다. 왜냐하면 후자는 투자에 선형적인 성장을 제공하기 때문입니다. 복리 이자는 기하 급수적인 성장을 제공합니다.
다음 이미지는 이러한 차이점을 보여줍니다.
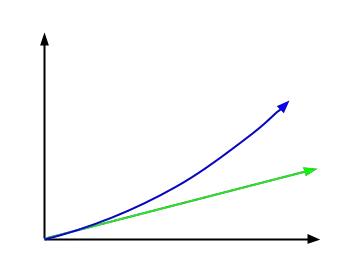
실제로 복리 이자는 초기 자본금 과 이미 벌어들인 이자를 합산 하여 적용됩니다. 예를 들어, €5,000를 투자하고 첫 해에 7%의 수익을 얻었다면 이자로 인해 €350가 창출되었기 때문에 자본금은 €5,350가 됩니다.
그러나 다음 해에도 동일한 수익성 비율(7%)을 얻으면 이자는 €350에서 €374.5로 증가합니다. 그러면 획득한 자본금은 5,350 + 374.5 = €5,724.5가 됩니다. 관심이 높아지고 있다는 뜻이다. 그러나 단순 이자는 매년 동일한 이자를 제공합니다.
복리 이자는 어떻게 계산되나요?
복리 계산은 비교적 간단한 과정입니다. 초기 금액, 연간 기여금, 이자율 및 투자 기간(보통 연 단위) 이라는 네 가지 변수 만 알면 됩니다. 그런 다음 다음 섹션에 표시된 공식을 적용하면 됩니다.
복리 공식
복리 이자 공식을 사용하면 특정 기간 동안 초기 원금에 대해 얻은 이자를 계산할 수 있습니다. 공식은 다음과 같습니다.
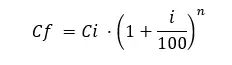
금:
Cf = 투자로 얻은 최종 자본.
C = 초기 자본.
i = 백분율로 표시된 연간 이자율(백분율을 100으로 나누어 백분율을 1로 얻음)
n = 투자 시간.
그러나 변수 “연간 기여금”을 고려하는 또 다른 공식도 있습니다. 정기적으로 투자에 기여 하려는 경우에만 사용해야 합니다. 예를 들어 처음에는 €1,000를 투자하고 이후에는 매년 €1,000를 투자합니다. 따라서 이전 수식은 적합하지 않으므로 다음을 사용해야 합니다.
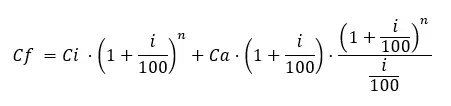
여기서 변수는 다른 식과 동일하며 Ca=연간 기부금액을 더한다.
이 두 번째 표현은 훨씬 더 복잡해 보이지만 실제로는 거의 같습니다. 실제로, 연간 기부금이 창출하는 금액을 추가하는 것은 이전 공식입니다.
복리 계산의 실제 예
복리 이자는 투자로부터 이익을 얻는 데 매우 유용한 도구입니다. 다음은 첫 번째 공식을 사용하여 복리를 계산하는 예입니다.
우리는 당신이 연 5%의 이자를 지급하는 은행에 €100를 가지고 있다고 가정합니다. 첫 해 말에 은행이 귀하에게 €5(€100의 5%)의 이자를 지불했기 때문에 귀하의 계좌에는 €105가 있게 됩니다.
두 번째 해가 시작될 때 귀하의 계좌에는 여전히 €105가 남아 있지만 이제 그 돈으로 인해 더 많은 이자가 발생합니다. 보다 정확하게는 연 5%의 이자를 적용하면 €5.25(105의 5%)의 이자를 얻게 됩니다. 즉, 두 번째 해 말에는 귀하의 계정에 총 €110.25가 있게 됩니다.
그리고 이 과정을 몇 년 동안 반복하면 기하 급수적 연산 이기 때문에 점점 더 많은 관심이 생길 것입니다. 따라서 복리로 인해 초기 자본에 대한 단순이자보다 훨씬 더 높은 수익을 얻을 수 있음을 알 수 있습니다.
복리의 장점은 무엇입니까?
복리의 장점은 “이익을 재투자하면 더 많은 돈을 벌 수 있다”는 한 문장으로 요약할 수 있습니다.
복리 이자는 “이자에 대한 이자”이며 많은 투자 모델 의 기초입니다. €1,000를 투자하고 연간 10%의 수익을 창출하는 경우 수익을 계속 재투자하면 10년 후에 초기 자본이 거의 3배가 됩니다. 주머니에서 다른 것을 추가할 필요 없이.
복리를 활용하는 열쇠는 규율과 시간 입니다. 적은 금액으로 시작하여 정기적으로 투자하십시오. 시간이 지남에 따라 투자가 어떻게 증가하는지 확인할 수 있습니다.