이 페이지에서는 선의 점-기울기 방정식에 대한 공식과 이를 계산하는 다양한 방법을 찾을 수 있습니다. 또한, 여러 예시를 보시고 단계별로 풀어보는 연습문제를 통해 연습하실 수 있습니다.
선의 점-기울기 방정식에 대한 공식
선의 점-기울기 방정식은 선을 수학적으로 표현하는 방법입니다. 특히 선의 점-기울기 방정식을 찾으려면 선 위의 한 점의 기울기와 좌표만 있으면 됩니다.
선의 점-기울기 방정식의 공식은 다음과 같습니다.
![]()
금
![]()
는 선의 기울기이고
![]()
은 선 위의 한 점의 좌표입니다
![]()
예를 사용하여 선의 점-기울기 방정식이 어떻게 계산되는지 살펴보겠습니다.
- 점을 통과하는 선의 점-기울기 방정식을 작성하십시오.
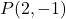
기울기 m=3입니다.
선의 점-기울기 방정식의 공식은 다음과 같습니다.
![]()
이 경우, 명령문은 선의 기울기가 m=3임을 알려주므로 선의 방정식은 다음과 같습니다.
![]()
게다가 우리는 선이 점을 통과한다는 것도 알고 있습니다.
![]()
, 따라서 이 점의 좌표를 방정식으로 대체해야 합니다.
![]()
![]()
따라서 선의 점-기울기 방정식은 다음과 같습니다.
![]()
점-기울기 방정식 외에도 벡터 방정식, 매개변수 방정식, 연속 방정식, 암시적 방정식(또는 일반) 및 선의 명시적 방정식 등 선을 분석적으로 표현하는 다른 방법이 있다는 점을 명심하세요. 더 관심이 있으시면 저희 웹사이트에서 각각의 내용을 확인하실 수 있습니다.
선의 기울기는 무엇을 의미하나요?
선의 점-기울기 방정식 정의에서 보았듯이 매개변수는
![]()
선의 기울기입니다. 그런데 정말… 선의 기울기가 무슨 뜻일까요? 선의 그래픽 표현을 통해 이를 살펴보겠습니다.
선의 기울기는 가파른 정도를 나타냅니다. 그래프 선에서 볼 수 있듯이,
![]()
1 수평 단위에 대해 선이 2 수직 단위만큼 상승하므로 2와 같습니다.
분명히, 기울기가 양수이면 함수는 증가(상승)하고, 반면에 기울기가 음수이면 함수는 감소(하향)합니다.
선의 기울기를 계산하는 방법
또한 선의 기울기를 수치적으로 결정하는 세 가지 방법이 있습니다.
- 선에 두 개의 서로 다른 점이 주어졌을 때

그리고

선의 기울기는 다음과 같습니다.
- 응

는 선의 방향 벡터이고 기울기는 다음과 같습니다.
- 응

는 가로축(X축)과 선이 이루는 각도이며, 선의 기울기는 해당 각도의 접선과 동일합니다.
![]()
![]()
![]()

선의 상대적 위치
마지막으로, 선의 기울기는 여러 선 사이의 관계를 아는 데에도 사용됩니다. 두 개의 평행선 은 동일한 기울기를 갖기 때문에, 반면에 한 선의 기울기가 다른 선의 기울기의 음의 역수라면 이는 이 두 선이 수직 임을 의미합니다.


두 점을 통과하는 선의 점-기울기 방정식을 계산합니다.
매우 일반적인 문제는 선에 속하는 두 점에서 점-기울기 방정식을 결정하는 것입니다. 예제를 통해 어떻게 해결되는지 살펴보겠습니다.
- 다음 두 점을 통과하는 선의 점-기울기 방정식을 구합니다.
![]()
선의 점-기울기 방정식을 찾으려면 선의 기울기가 무엇인지 알아야 합니다. 따라서 콜론 공식을 사용하여 선의 기울기를 계산합니다.
![]()
따라서 선의 점-기울기 방정식은 다음과 같습니다.
![]()
![]()
따라서 선 위의 한 점의 데카르트 좌표를 방정식으로 대체하면 됩니다.
![]()
![]()
![]()
문장의 다른 점을 선의 방정식에 넣는 것도 좋습니다.
![]()
![]()
그래프에서 선의 점-기울기 방정식 찾기
위 섹션에서 살펴본 것처럼 선의 점-기울기 방정식을 수치적으로 찾는 방법에는 여러 가지가 있습니다. 그러나 그래픽으로도 찾을 수 있습니다. 예제를 통해 이것이 어떻게 수행되는지 살펴보겠습니다.
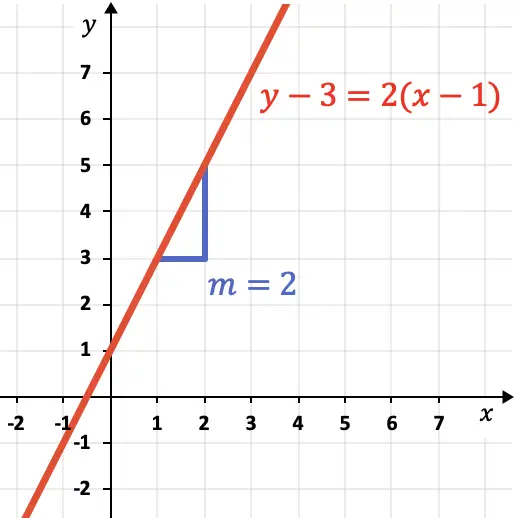
- 다음 그래프에 표시된 선의 점-기울기 방정식을 결정합니다.
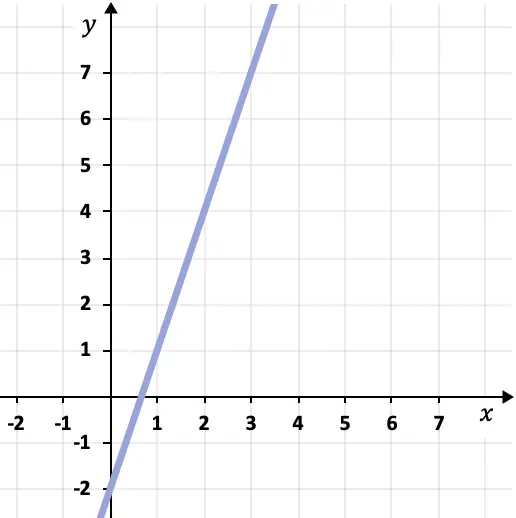
그려진 선의 점-기울기 방정식을 결정하려면 선의 기울기와 선 위의 점을 찾아야 합니다.
이 경우 선의 기울기는 3과 같습니다. 왜냐하면 선은 수평 단위마다 3 수직 단위만큼 올라가기 때문입니다.
![]()
다음으로 선 위에 점이 필요합니다. 이를 위해 선이 통과하는 그래프의 임의의 점(예: 점 (1,1))을 선택할 수 있습니다.
![]()
따라서 이제 공식을 적용하여 선의 점-기울기 방정식을 찾을 수 있습니다.
![]()
![]()
해결된 점-기울기 방정식 문제
연습 1
점을 통과하는 선의 점-기울기 방정식을 작성하십시오.
![]()
그리고 그 기울기는
![]()
선의 점-기울기 방정식에 대한 공식은 다음과 같습니다.
![]()
이 경우, 명령문은 선의 기울기가 m=-2임을 알려주므로 선의 방정식은 다음과 같습니다.
![]()
또한, 우리는 선이 점을 통과한다는 진술을 통해 알 수 있습니다.
![]()
, 따라서 점의 좌표를 선의 방정식으로 대체하는 것으로 충분합니다.
![]()
![]()
연습 2
다음 두 점을 지나는 직선의 점-기울기 방정식은 무엇입니까?
![]()
선의 점-기울기 방정식을 찾으려면 선의 기울기가 무엇인지 알아야 합니다. 따라서 다음 공식을 사용하여 선의 기울기를 계산합니다.
![]()
따라서 선의 점-기울기 방정식은 다음과 같습니다.
![]()
![]()
따라서 방정식에 선 위의 점 좌표를 대입하면 됩니다.
![]()
![]()
또한 진술의 다른 점을 방정식에 넣는 것도 정확했을 것입니다.
![]()
연습 3
다음 두 점을 통과하는 선의 점-기울기 방정식을 구합니다.
![]()
선의 점-기울기 방정식을 찾으려면 먼저 기울기를 계산해야 합니다.
![]()
따라서 선의 점-기울기 방정식은 다음과 같습니다.
![]()
![]()
따라서 방정식에 선 위의 점 좌표를 대입하면 됩니다.
![]()
![]()
![]()
직선의 방정식에 있는 진술의 다른 점을 넣는 것도 옳습니다.
![]()
연습 4
X축과 45°의 각도를 이루며 좌표 원점을 통과하는 선의 점-기울기 방정식을 계산합니다.
선이 OX 축과 45도 각도를 이루면 기울기는 다음과 같습니다.
![]()
![]()
![]()
그리고 선의 기울기를 알면 선 위의 점을 방정식에 대입하여 점-기울기 방정식을 찾을 수 있습니다. 또한 이 명령문은 선이 좌표 원점을 통과한다는 것을 알려줍니다. 이는 점(0,0)을 통과한다는 의미입니다. 아직:
![]()
![]()
따라서 선의 점-기울기 방정식은 다음과 같습니다.
![]()
연습 5
직선과 평행한 직선의 점 기울기 방정식을 구합니다.
![]()
그리고 그 지점에서 무슨 일이 일어나는지
![]()
똑바로하다
![]()
![]()
선의 기울기
![]()
는 2(괄호 앞의 숫자)와 동일하며 두 선이 평행하려면 기울기가 같아야 합니다. 따라서 다음과 같습니다.
![]()
![]()
그리고 선의 기울기를 알고 나면 선에 속하는 점의 좌표를 공식에 대입하면 됩니다.
![]()
![]()
따라서 선의 점-기울기 방정식은 다음과 같습니다.
![]()
연습 6
다음 그래프에 표시된 각 선에 대한 점-기울기 방정식을 결정합니다.

파란색 오른쪽
파란색 선은 각 X에 대해 1 Y씩 증가하므로 기울기는 1과 같습니다. 반면에 점 (2,4)를 통과하므로 다음과 같습니다.
![]()
오른쪽 녹색
녹색 선은 X마다 Y가 3씩 증가하므로 기울기는 3입니다. 또한 점 중 하나는 (2,2)이므로 다음과 같습니다.
![]()
레드 라인
빨간색 선은 X마다 2Y씩 감소하므로 기울기는 -2입니다. 그리고 점 (0,-2)는 이 선에 속합니다. 따라서:
![]()