이 페이지에서는 매개변수를 기반으로 테이블의 순위를 계산하는 방법을 살펴보겠습니다. 또한 하나의 매개변수를 기반으로 행렬의 범위를 찾는 방법에 대한 단계별 예제와 해결 연습도 찾아볼 수 있습니다.
매개변수가 있는 행렬의 순위를 연구하는 절차를 완전히 이해하려면 행렬식에 따라 행렬의 순위를 계산하는 방법을 이미 알고 있는 것이 중요합니다. 따라서 계속 읽기 전에 먼저 이 두 가지 사항을 학습하는 것이 좋습니다.
매개변수를 기반으로 배열의 범위를 계산하는 방법 예:
- 다양한 매개변수 값을 기반으로 행렬 A의 범위를 결정합니다.
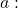
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0aa5688f2845a0225149f448466c943c_l3.png)
행렬 A는 3차 행렬이기 때문에 최대 랭크 3이 됩니다. 따라서 우리가 해야 할 첫 번째 일은 전체 3×3 행렬의 행렬식을 Sarrus의 법칙 으로 풀어서 그것이 랭크 3이 될 수 있는지 확인하는 것입니다:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-835a881061438326519f4660b4c394fc_l3.png)
행렬식의 결과는 매개변수의 함수입니다.
![]()
. 따라서 테이블이 언제 순위 2가 되고 언제 순위 3이 될지 확인하기 위해 결과를 0으로 설정합니다 .
![]()
그리고 우리는 결과 방정식을 푼다:
![]()
![]()
![]()
그러므로 언제
![]()
+1이든 -1이든 3×3 행렬식은 0이 되고 따라서 행렬의 순위는 3이 되지 않습니다.
![]()
가 +1 및 -1과 다르면 행렬식은 0과 다르므로 행렬은 순위 3이 됩니다.
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-53dde6f61dc01cac5c0a0705c44a7433_l3.png)
이전에 살펴보았듯이, 언제
![]()
1이면 행렬의 행렬식은 0입니다. 따라서 순위 3이 될 수 없습니다. 이제 행렬 내부의 0과 다른 2×2 행렬식을 계산하려고 합니다(예: 왼쪽 상단 모서리).
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d291f322f9d3f392e46568817e531a84_l3.png)
차수 2의 행렬식은 0과 다릅니다. 따라서 매개변수가
![]()
또는 +1이면 행렬의 순위는 2가 됩니다.
![]()
일단 행렬의 범위를 보면
![]()
그리고 언제
![]()
언제 무슨 일이 일어나는지 봅시다
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f723d9c6b9f786b8c405ac7ec2d8bf1d_l3.png)
처음에 봤듯이,
![]()
es -1이고 행렬의 행렬식은 0이다. 따라서 랭크 3으로 설정할 수 없다. 따라서 0과 다른 행렬에서 2×2의 행렬식을 만나도록 노력해야 한다. 매트릭스의 일부. 왼쪽:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdc9bd6d9ad083e1e38f53079aebb5e5_l3.png)
차원 2의 행렬식은 0과 다릅니다. 따라서 매개변수가
![]()
또는 -1이면 테이블 순위는 2가 됩니다.
![]()
따라서 우리는 행렬 A의 순위가 매개변수가 취하는 값에 따라 달라지는 3가지 다른 경우를 발견했습니다.
![]()
요약은 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc3a7ebea32c871ab7971a276decc60a_l3.png)
이제 매개변수 종속 행렬의 범위를 논의하는 방법을 알았으므로 아래의 단계별 연습을 연습할 수 있습니다. 이 문제를 해결하려면 한정자의 속성이 도움이 될 것입니다. 따라서 이에 대해 명확하지 않은 경우 먼저 링크된 페이지를 살펴보는 것이 좋습니다. 각 페이지에는 예제가 설명되어 있습니다.
매개변수 기반 매트릭스 범위 문제 수정
연습 1
매개변수 값을 기준으로 다음 표의 범위를 연구합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d7f53b08bcf2e2660dbb7c0aeb6fd369_l3.png)
행렬 A는 3×3 행렬이기 때문에 최대 순위 3을 갖습니다. 따라서 우리가 해야 할 첫 번째 일은 전체 행렬의 행렬식을 (Sarrus의 규칙을 사용하여) 풀어서 순위 3이 될 수 있는지 확인하는 것입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2539698cbcf9f06d2890d17da76174f_l3.png)
배열이 언제 랭크 2가 되고 언제 랭크 3이 되는지 확인하기 위해 결과를 0으로 설정합니다.
![]()
![]()
![]()
그러므로 언제
![]()
가 2와 다르면 행렬식 3×3은 0과 다르므로 행렬의 순위는 3이 됩니다.
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c131e19dd5d5c0d7826306103b4e118b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-b97f01989b5e9679f95d300cd64f3735_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-77b38ebf03b8ed059edefd523c5ca1f4_l3.png)
![]()
따라서 우리는 행렬 A의 범위가 매개변수가 취하는 값에 따라 달라지는 2가지 경우를 발견했습니다.
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-41e5cc7b6e9b3204f26e1c64e46f7057_l3.png)
연습 2
매개변수 값을 기준으로 다음 표의 범위를 구합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b28f21cc2e7211d9dae9b6685b541fc_l3.png)
행렬 A는 3×3 행렬이기 때문에 최대 순위 3을 갖습니다. 따라서 우리가 해야 할 첫 번째 일은 전체 행렬의 행렬식을 (Sarrus의 규칙을 사용하여) 풀어서 순위 3이 될 수 있는지 확인하는 것입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-30c8c16fea09001059a5d66727fc7be3_l3.png)
배열이 언제 랭크 2가 되고 언제 랭크 3이 되는지 확인하기 위해 결과를 0으로 설정합니다.
![]()
![]()
![]()
![]()
![]()
그러므로 언제
![]()
가 +1 및 -1과 다르면 3×3 행렬식은 0과 다르므로 행렬의 순위는 3이 됩니다.
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b95d408f076c4978c8605380a277cdf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcd50b9549925b5011a6c20943c326ee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03242296f208e07b9c4d634f0b7724cc_l3.png)
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2d16421400df26760d811229215ac83_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ecd0b86cd6c59a0911f0c39ca7599806_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-378e43f0ef61ccabf82dacb5ac70466f_l3.png)
![]()
따라서 우리는 매개변수가 취하는 값에 따라 행렬 A의 범위가 달라지는 3가지 경우를 발견했습니다.
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bf1904cee51914e041d94f588fed84d_l3.png)
연습 3
매개변수 값을 기준으로 다음 표의 범위를 계산합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-090a99d3b4111785433e5c769589eb01_l3.png)
행렬 A는 3×3 행렬이기 때문에 최대 순위 3을 갖습니다. 따라서 우리가 해야 할 첫 번째 일은 전체 행렬의 행렬식을 (Sarrus의 규칙을 사용하여) 풀어서 순위 3이 될 수 있는지 확인하는 것입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fec1cb52bb87fa2bccb40b70e1f21c7c_l3.png)
배열이 언제 랭크 2가 되고 언제 랭크 3이 되는지 확인하기 위해 결과를 0으로 설정합니다.
![]()
이것은 불완전한 이차 방정식이므로 공통 인수를 추출합니다.
![]()
그리고 각 항을 0으로 설정합니다.
![Rendered by QuickLaTeX.com \displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43b38da320da538e46c6b4515de48568_l3.png)
우리는 해로 0과 -4를 얻었습니다. 그러므로 언제
![]()
가 0과 -4와 다르면 3×3 행렬식은 0과 다르므로 행렬의 순위는 3이 됩니다.
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d97b25f01cb00d4677da0de5b4340ddb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0f3c315588dff8274873001f727a69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c132b22650c707d9f410c3d9c1e8da35_l3.png)
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ce7e40d9d78ecddc5ee81fc799c8767_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-52d15d0bceeb1dbbc415fb4825ce9a05_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d45971f1dbda32405246de38bb68bd92_l3.png)
![]()
따라서 우리는 매개변수가 취하는 값에 따라 행렬 A의 범위가 달라지는 3가지 경우를 발견했습니다.
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-844f152985a2d84be1456501dfdc16e4_l3.png)
연습 4
매개변수의 값에 따라 다음 3×4 차원 행렬의 범위를 구합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4da7907bd0e8f80006ea47d2437b3f3d_l3.png)
행렬 A는 4×4 행렬식을 계산할 수 없기 때문에 최대 순위 3에 있습니다. 따라서 우리가 해야 할 첫 번째 일은 차수 3의 가능한 모든 행렬식(Sarrus의 규칙 사용)을 풀어 차수 3이 될 수 있는지 확인하는 것입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2db025b8ecf4323d4a912d84a215d8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e40592bf6f8bfd13cb68a1fd0393cebb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce1c28ae4120f0b37059b763e576d2eb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-668e9096b00b90ee4cc48d272b17e7bd_l3.png)
3차의 가능한 모든 행렬식의 결과는 값에 관계없이 0입니다.
![]()
. 따라서 행렬은 어떤 값을 취하는지는 중요하지 않기 때문에 결코 랭크 3이 될 수 없습니다.
![]()
0이 아닌 3×3 행렬식은 절대 존재하지 않습니다.
이제 우리는 차원 2 × 2의 행렬식을 시도합니다. 그러나 차수 2의 모든 행렬식도 다음을 제외하고 0을 제공합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4408f1ccf562196943209356e50e892_l3.png)
이제 결과를 0으로 설정하고 방정식을 풉니다.
![]()
![]()
![]()
그러므로 언제
![]()
가 -2와 다르면 행렬식 2×2는 0과 다르므로 행렬의 순위는 2가 됩니다.
![]()
이제 언제 무슨 일이 일어나는지 봅시다.
![]()
![Rendered by QuickLaTeX.com \displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ecbf63b188b46c05e67741cee83d7a2_l3.png)
이전에 살펴보았듯이, 언제
![]()
가 -2이면 2차 행렬식은 모두 0입니다. 따라서 순위 2가 될 수 없습니다. 그리고 0과 다른 1×1 행렬식이 하나 이상 존재하므로 이 경우 행렬의 순위는 1입니다.
![]()
따라서 우리는 행렬 A의 범위가 매개변수가 취하는 값에 따라 달라지는 2가지 경우를 발견했습니다.
![Rendered by QuickLaTeX.com \displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-2bdfb67894431a4a08a3e791dcda0313_l3.png)