이 기사에서는 Weierstrass 정리의 정의를 찾을 수 있습니다. 또한, Weierstrass 정리를 단계별로 풀어내는 여러 연습문제를 통해 실습을 통해 완벽하게 이해할 수 있게 됩니다.
Weierstrass의 정리에 대한 설명
Weierstrass의 정리에 따르면 함수가 닫힌 구간에서 연속인 경우 해당 함수는 해당 구간에서 절대 최대값과 절대 최소값을 갖습니다.
➤ 참고: 연속함수란 무엇입니까?
Weierstrass의 정리는 최대값과 최소값이 있다는 것만 명시하고 이러한 점의 값을 계산하는 것은 유용하지 않습니다.
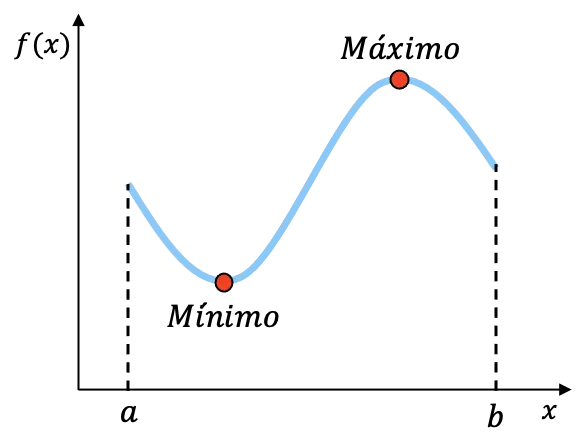
예를 들어, 위에 그래프로 표시된 함수는 구간 [a,b]에서 연속이고 이 구간에서 최소값과 최대값을 갖습니다. 이 두 점의 정확한 좌표를 알 수는 없지만 함수의 구간에 이 두 끝점이 있다는 것을 알고 있습니다.
➤ 참조: 함수의 최대값과 최소값을 계산하는 방법
함수가 전체 간격에 걸쳐 연속적이므로 동일한 간격에 걸쳐 절대 최소값과 절대 최대값 사이의 가능한 모든 값도 취하게 됩니다.
또한 Weierstrass 정리의 결과로 닫힌 구간의 모든 연속 함수는 위와 아래의 경계를 가지며 함수의 상한과 하한은 각각 절대 최대값과 최소값임을 추론할 수 있습니다.
수학적으로 Weierstrass의 정리는 다음과 같이 표현될 수 있습니다.
![]()
금
![]()
그리고
![]()
닫힌 구간에 포함된 두 점(각각 절대 최소값과 절대 최대값)입니다.
![]()
함수가 정의되어 있는 곳입니다.
Weierstrass 정리의 증명은 상당히 복잡하고 개념에 많은 기여를 하지 않으므로 이 기사에서는 설명하지 않습니다. 중요한 것은 Weierstrass 정리가 무엇인지, 그리고 그것이 어디에 사용되는지 이해하는 것입니다.
Weierstrass 정리로 문제 해결
연습 1
다음 함수가 제안된 구간에 제한되어 있는지 확인합니다.
![]()
➤ 참고: 로그 함수의 영역
Weierstrass 정리를 적용하여 함수가 구간 [5,10]에 국한되어 있는지 확인할 수 있습니다. 따라서 우리는 함수가 이 구간에서 연속인지 알아야 합니다. 이를 위해 로그 함수의 영역을 계산합니다.
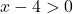
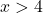
![]()
이 함수는 x=4보다 큰 모든 값에 대해 연속이므로 구간 [5,10]에서 연속입니다.
따라서 함수는 구간 [5,10]에서 Weierstrass의 정리를 만족합니다. 즉, 이 구간에서 위와 아래에 경계가 있음을 의미합니다.
연습 2
다음 함수가 제안된 간격에 걸쳐 최대값 및/또는 최소값을 갖는지 확인합니다.
![]()
➤ 참고: 유리함수의 영역
먼저 유리 함수의 연속성을 분석합니다.
![]()
![]()
![]()
![]()
그러나 이 함수는 x=2에서 불연속성을 나타내며, 이는 구간 [-3,3]에서 연속되지 않음을 의미합니다.
즉, 함수는 Weierstrass의 정리를 만족하지 않으므로 이 구간에서 최소값 또는 최대값을 갖는지 여부를 말할 수 없습니다.
연습 3
다음 함수가 제안된 구간에서 최대값 및/또는 최소값을 갖는지 확인하고 다음 점을 계산합니다.
![]()
➤ 참조: 이차 함수의 특성
모든 이차 함수의 정의역은 모두 실수입니다:
![]()
따라서 함수는 구간 [0,4]에서 연속이고 Weierstrass 정리를 충족합니다. 따라서 함수는 이 구간에서 절대 최소값과 절대 최대값을 갖습니다.
또한 이 포물선의 꼭지점은 정확히 x=0에 있으므로 함수는 간격 [0,4]에서 엄격하게 증가하며 결과적으로 최소값은 x=0에 있고 최대값은 x= 4에 있습니다.
![]()
![]()
칼 바이어슈트라스
Weierstrass 정리가 무엇을 의미하는지 확인한 후에는 이 정리의 목록이 누구인지 간략하게 설명하겠습니다.
카를 테오도르 빌헬름 바이어스트라스(Karl Theodor Wilhelm Weierstrass) 는 19세기 독일의 매우 중요한 수학자였습니다. 보다 정확하게는 1815년 10월 31일 오스텐펠데에서 태어나 1897년 2월 19일 베를린에서 사망했습니다.
Weierstrass의 정리 외에도 그는 수학에 대한 다른 공헌으로도 유명합니다. 그 중에서 그는 함수의 세 가지 매우 중요한 개념인 연속성, 극한, 미분의 정의를 제시했습니다.
마찬가지로 그는 Bolzano-Weierstrass 정리, 평균값 정리 또는 Heine-Borel 정리와 같이 당시 아직 수학적으로 검증되지 않은 특정 정리를 입증했습니다.
호기심으로 달 분화구와 그를 기리기 위해 바이어슈트라스의 이름을 딴 소행성이 있습니다.