대칭행렬 - 수학

이 페이지에서는 대칭 행렬이 무엇인지 설명합니다. 또한 의심의 여지가 없도록 몇 가지 예와 함께 행렬이 대칭인 경우를 빠르게 식별하는 방법을 보여줍니다. 또한 대칭 행렬의 모든 속성을 찾을 수 있습니다. 그리고 마지막으로 모든 정사각 행렬이 갖는 특별한 특징을 설명합니다. 즉, 대칭 행렬과 반대칭 행렬의 합으로 분해될 수 있습니다.

대칭 행렬이란 무엇입니까?

대칭행렬의 정의는 다음과 같습니다.

대칭 행렬은 전치가 행렬 자체와 동일한 정사각 행렬입니다.

$A^t = A$

금

$A^t$

전치된 행렬을 나타냅니다.

$A$

대칭 행렬의 개념을 알게 되면 대칭 행렬을 어떻게 쉽게 식별할 수 있는지 살펴보겠습니다.

행렬이 대칭인 경우는 언제입니까?

대칭 행렬의 구조를 인식하는 것은 매우 간단합니다. i 행과 j 열의 요소는 j 행과 i 열의 요소와 동일해야 합니다. 그리고 행렬의 주대각선 값은 무엇이든 될 수 있습니다.

대칭 행렬의 예

다음은 이해를 돕기 위한 대칭 행렬의 몇 가지 예입니다.

2 × 2 차 대칭 행렬의 예

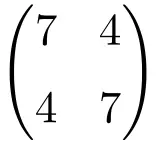
차원 3×3의 대칭 행렬의 예

크기가 4×4인 대칭 행렬의 예

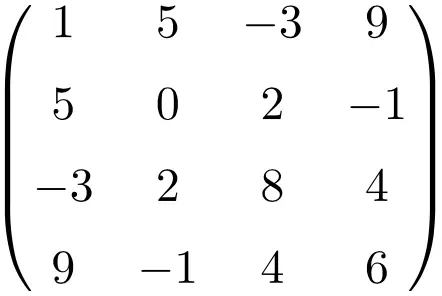
이 세 가지 행렬을 전치함으로써 우리는 이들이 대칭임을 확인합니다. 왜냐하면 전치된 행렬이 각각의 원래 행렬과 동일하기 때문입니다.

왜 대칭행렬이라고 불리는가?

이전 예를 자세히 살펴보면 대칭행렬의 주대각선은 대칭축, 즉 대각선 위의 숫자와 아래의 숫자 사이의 거울 역할을 합니다. 이러한 이유로 이러한 유형의 행렬을 대칭 행렬이라고 합니다.

대칭 행렬의 속성

대칭행렬의 특징은 다음과 같습니다.

두 개의 대칭 행렬을 더하거나 빼면 또 다른 대칭 행렬이 생성됩니다. 두 개의 더해진(또는 뺀) 행렬을 전치하는 것은 각 행렬을 개별적으로 전치하는 것과 동일하므로:

$\displaystyle \left(A+B\right)^t = A^t+B^t = A+B$

스칼라를 곱한 대칭 행렬은 또 다른 대칭 행렬을 생성합니다.

마찬가지로, 두 대칭 행렬 사이의 행렬 곱은 두 행렬이 교환될 수 있는 경우에만 다른 대칭 행렬과 항상 동일하지는 않습니다. 이 조건은 전치 행렬 곱셈 속성을 사용하여 증명할 수 있습니다.

$\displaystyle \left(A\cdot B\right)^t = B^t\cdot A^t = BA=AB$

지수가 정수인 한 대칭 행렬의 거듭제곱은 또 다른 대칭 행렬을 발생시킵니다.

분명히 유니터리 행렬 과 제로 행렬은 대칭 행렬의 예입니다.

대칭행렬과 합동인 행렬은 또한 대칭행렬이어야 합니다.

대칭 행렬이 정칙이거나 가역적이면 역행렬도 대칭입니다.

이는 대칭 행렬의 수반 행렬과 동일합니다. 대칭 행렬의 수반 행렬은 해법으로 또 다른 대칭 행렬을 제공합니다.

진정한 대칭행렬은 정규행렬이기도 합니다.

대칭 행렬은 에르미트 행렬의 특별한 경우이므로 대칭 행렬의 고유값(또는 고유값)은 모두 실수입니다.

스펙트럼 정리는 요소가 실수인 모든 행렬이 대각화 가능한 행렬이며, 또한 대각화는 직교 행렬을 통해 수행된다는 것을 알려줍니다. 따라서 모든 실수 대칭 행렬은 직교 대각선화됩니다.

반면, 복소수를 갖는 대칭 행렬은 단일 행렬을 통해 대각화될 수 있습니다.

헤세 행렬은 항상 대칭입니다.

정사각 행렬을 대칭 행렬과 반대칭 행렬로 분해

정사각 행렬의 특별한 특징은 대칭 행렬과 반대칭 행렬의 합으로 분해될 수 있다는 것입니다.

이를 가능하게 하는 공식은 다음과 같습니다.

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

여기서 C는 분해하려는 정사각 행렬이고, C ^는 전치 행렬이며, 마지막으로 S와 A는 각각 행렬 C가 분해되는 대칭 행렬과 반대칭 행렬입니다.

아래에는 이것이 어떻게 수행되는지 확인하기 위한 해결된 연습이 있습니다. 다음 행렬을 분해해 보겠습니다.

$\displaystyle C=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

다음 공식을 사용하여 대칭 및 반대칭 행렬을 계산합니다.

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}$

그리고 두 행렬을 추가하여 방정식이 충족되는지 확인할 수 있습니다.

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 2& 1 \\[1.1ex] 1 &0\end{pmatrix}+\begin{pmatrix} 0& -2 \\[1.1ex] 2 &0\end{pmatrix}=\begin{pmatrix} 2& -1 \\[1.1ex] 3 &0\end{pmatrix}$

$\displaystyle C=S+A$

✅