이 페이지에서는 널 행렬이라고도 불리는 제로 행렬에 대한 설명을 찾을 수 있습니다. 또한 해당 요소의 값이 행렬의 차원과 무관하다는 것을 예제를 통해 확인할 수 있으며 마지막으로 이러한 유형의 행렬의 모든 속성을 찾을 수 있습니다.
널 행렬이란 무엇입니까?
널 행렬 (또는 널 행렬)은 요소가 모두 0인 행렬입니다.
따라서 영행렬의 정의에 따르면 이 행렬은 모든 숫자가 0인 한 가능한 모든 차원을 가질 수 있습니다. 다음 예를 살펴보십시오.
널 행렬의 예
2 × 2 널 행렬의 예
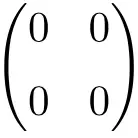
3 × 3 널 행렬의 예
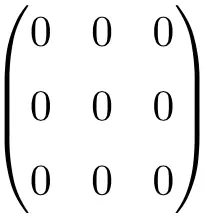
4 × 4 널 행렬의 예
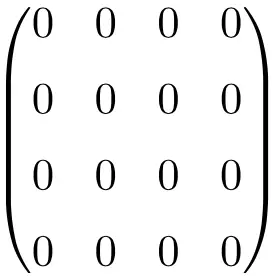
이제 이 특별한 행렬은 단순히 0으로 가득 찬 행렬이기 때문에 중요하지 않은 것처럼 보일 수 있습니다. 그러나 수학, 특히 선형 대수학 분야에서는 계산을 훨씬 쉽게 만들어주기 때문에 매우 유용한 행렬입니다.
널 행렬의 속성
Null(또는 Null) 행렬에는 다음과 같은 특징이 있습니다.
- 제로 행렬은 행렬 추가 연산의 중립 요소이므로 다음과 같습니다.
![]()
- 행렬 곱셈은 0의 곱셈 속성을 갖습니다. 즉, 0 행렬에 행렬을 곱한 결과는 0과 같습니다.
![]()
- 행렬이 정사각형인 경우 영행렬은 대칭 및 반대칭을 모두 갖습니다.
- 제로 행렬은 순위가 0인 유일한 행렬입니다.
- 영행렬의 행렬식은 항상 0으로 평가되므로 이 유형의 행렬에는 역행렬이 없습니다(단일 행렬임).
- 분명히 영행렬은 무능행렬의 한 예 이다.