이 글에서 우리는 함수의 경사 점근선이 무엇인지 설명합니다. 함수에 경사 점근선이 있는 경우와 이를 계산하는 방법을 알아봅니다. 그리고 추가적으로 경사 점근선의 예를 볼 수 있고, 단계별로 풀어가는 연습문제를 통해 연습할 수 있습니다.
경사 점근선이란 무엇입니까?
함수의 경사 점근선은 그래프가 교차하지 않고 무한정 접근하는 경사선입니다. 결과적으로, 모든 경사 점근선은 방정식 y=mx+n 을 갖는 선입니다.
경사 점근선의 기울기와 원점은 다음 공식을 사용하여 계산됩니다.
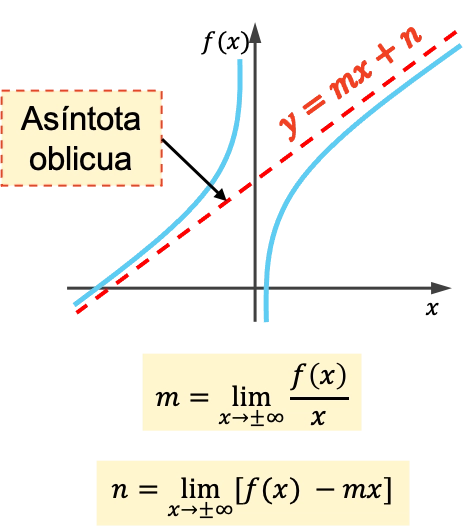
함수의 경사 점근선을 계산하는 방법
함수의 경사 점근선을 계산하려면 다음 단계를 수행해야 합니다:
- x로 나눈 함수의 무한대 극한을 계산합니다.
- 위의 극한으로 인해 0이 아닌 실수가 발생하는 경우 이는 함수에 경사 점근선이 있음을 의미합니다. 그리고, 상기 경사 점근선의 기울기는 극한에서 구해지는 값이 됩니다.
- 이 경우, 남은 것은 다음 극한을 풀어 경사 점근선의 절편을 계산하는 것뿐입니다.
![]()
![]()
참고: 극한은 플러스 및 마이너스 무한대에서 계산되어야 하지만 일반적으로 동일한 결과를 제공하므로 ±무한대를 넣어 단순화합니다. 그러나 플러스와 마이너스 무한대의 극한이 다른 경우 왼쪽 경사 점근선과 오른쪽 경사 점근선은 별도로 계산되어야 합니다.
경사 점근선 예
다음으로, 이것이 어떻게 수행되는지에 대한 예를 볼 수 있도록 다음 유리 함수의 경사 점근선을 취하겠습니다.
![]()
경사 점근선은 다음 유형입니다.
![]()
먼저 선의 기울기를 계산합니다.
![]()
해당 공식을 사용하면 다음과 같습니다.
![]()
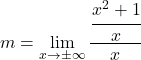
이 한계를 해결하려면 분수의 속성을 적용해야 합니다.
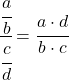
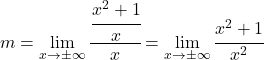
이제 한계를 계산합니다.
![]()
이 경우, 무한대 사이의 무한대의 불확정성의 결과는 분자와 분모가 동일한 차수이기 때문에 가장 높은 x의 계수를 나누는 것입니다.
위의 극한은 0이 아닌 실수를 제공하므로 함수는 경사 점근선을 갖습니다. 이제 y절편을 계산해 보겠습니다.
![]()
해당 공식을 사용하여 점근선을 계산합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9197669cc0e41aa22224b552b21b31ed_l3.png)
우리는 한계를 계산하려고 합니다:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d7fa012eace37e82c243012c91f1a5c_l3.png)
그러나 우리는 불확정성 무한대 마이너스 무한대를 얻습니다. 따라서 용어를 공통 분모로 줄이는 것이 필요합니다. 이를 위해 x를 분수의 분모로 곱하고 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2355ed9411470b9fd20a50ebbd48726_l3.png)
이제 두 용어의 분모가 동일하므로 그룹화할 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f932ebc8728669c7c6b57e115c444fc7_l3.png)
우리는 분자에 대해 작업합니다:
![]()
마지막으로 한계를 해결합니다.
![]()
따라서 n =0입니다. 따라서 경사 점근선은 선형 함수입니다.
![]()
![]()
![]()
연구된 함수는 아래 그래프에 표시됩니다. 보시다시피, 함수는 y=x 선에 매우 가깝지만 경사 점근선이기 때문에 절대 건드리지 않습니다:

경사 점근선에 대한 해결된 연습
연습 1
다음 유리 함수의 경사 점근선을 구합니다:
![]()
경사 점근선의 형식은 다음과 같습니다.
![]()
따라서 매개변수 m 과 n 을 계산해야 합니다. 먼저 다음 공식을 적용하여 m을 계산합니다.
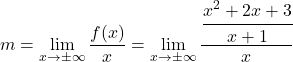
분수의 속성을 적용하여 분수를 단순화합니다.
![]()
![]()
그리고 우리는 한계를 해결합니다:
![]()
그래서 m =1입니다. 이제 공식을 적용하여 경사 점근선의 절편을 계산해 보겠습니다.
![]()
우리는 한계를 계산하려고 합니다:
![]()
그러나 우리는 무한대에서 무한대를 뺀 부정확한 형태를 얻습니다. 따라서 용어를 공통 분모로 축소한 다음 그룹화해야 합니다.
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0712d34ed442d9e12ef2490f04df078a_l3.png)
마지막으로 한계를 해결합니다.
![]()
간단히 말해서, 함수의 경사 점근선은 다음과 같습니다:
![]()
![]()
![]()
연습 2
다음 유리 함수의 경사 점근선을 모두 찾습니다.
![]()
먼저, 경사 점근선의 기울기 공식을 사용합니다:
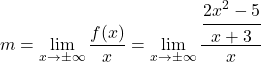
분수의 속성을 적용하여 분수를 단순화합니다.
![]()
![]()
그리고 우리는 한계를 결정합니다.
![]()
극한은 0이 아닌 실수를 제공하므로 기울기가 2인 경사 점근선을 갖는 유리 함수입니다.
이제 해당 공식을 적용하여 절편을 계산해 보겠습니다.
![]()
우리는 한계를 계산하려고 합니다:
![]()
그러나 우리는 무한대의 차이 불확정성을 얻습니다. 따라서 용어를 공통 분모로 축소한 후 다음과 같이 작동합니다.
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4920e8b21b180c4f2740ce712d9f30d0_l3.png)
마지막으로 한계를 해결합니다.
![]()
요약하면, 분수 함수의 경사 점근선은 다음과 같습니다.
![]()
![]()