역행렬을 계산하는 방법 -

이 페이지에서는 행렬식이 무엇인지, 행렬식(또는 수반 행렬) 방법과 가우스 방법을 사용하여 행렬의 역행렬을 계산하는 방법을 배웁니다. 또한 역행렬의 모든 속성을 볼 수 있으며, 완전히 이해할 수 있도록 각 방법에 대한 단계별 풀이 예제와 연습도 제공됩니다. 마지막으로, 2×2 행렬을 빠르게 반전시키는 공식과 이 행렬 연산의 가장 큰 유용성인 선형 방정식 시스템을 푸는 공식에 대해 설명합니다.

행렬의 역행렬은 무엇입니까?

$A$

정사각형 행렬. 역행렬

$A$

그것은 쓰여있다

$A^{-1}$

, 그리고 다음을 만족하는 것은 이 행렬입니다:

$A \cdot A^{-1} = I$

$A^{-1}\cdot A = I$

금

$I$

항등 행렬입니다.

언제 행렬을 반전할 수 있고 언제 반전할 수 없나요?

행렬의 가역성을 결정하는 가장 간단한 방법은 행렬식을 사용하는 것입니다.

문제의 행렬의 행렬식이 0과 다르다면, 이는 행렬이 가역적이라는 것을 의미합니다. 이 경우 우리는 그것이 정규 행렬이라고 말합니다. 또한 이는 행렬이 최대 순위임을 의미합니다.

반면에 행렬식의 값이 0이면 행렬을 반전시킬 수 없습니다. 그리고 이 경우에 우리는 그것이 특이행렬(Singular Matrix) 또는 퇴화행렬(Degenerate Matrix)이라고 말합니다.

주로 행렬을 반전시키는 방법에는 행렬식이나 수반행렬의 방법과 가우스 방법의 두 가지가 있습니다. 아래에는 첫 번째 설명이 있지만 가우스 방법을 사용하여 행렬을 반전시키는 방법도 아래에서 참조할 수 있습니다.

행렬식 방법을 사용하여(또는 인접 행렬을 사용하여) 행렬 반전

행렬의 역행렬을 계산하려면,

$\displaystyle A^{-1}$

, 다음 공식을 적용해야 합니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

금:

$\displaystyle \begin{vmatrix} A \end{vmatrix}$

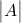
는 행렬의 행렬식이다

$A$
$\text{Adj}(A)$

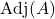
는 다음의 수반행렬이다:

$A$
전시자
$\bm{t}$

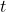
행렬 전치를 나타냅니다. 즉, 첨부된 행렬이 전치되어야 함을 나타냅니다.

설명: 일부 책에서는 약간 다른 역행렬 공식을 사용합니다. 먼저 수반 행렬을 계산한 다음 전치하는 대신 행렬 A를 전치한 다음 수행 행렬을 계산합니다. 실제로는 결과가 완전히 동일하기 때문에 순서는 중요하지 않습니다. 여기서는 수정된 행렬을 사용하려는 경우를 대비해 수정된 행렬을 반전시키는 공식을 남겨둡니다.

그런 다음 예제로 연습 문제를 풀어 역행렬을 찾는 방법을 살펴보겠습니다.

행렬식 방법(또는 수반 행렬)을 사용하여 역행렬을 계산하는 예:

다음 행렬의 역함수를 계산합니다.

$\displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}$

역행렬을 결정하려면 다음 공식을 적용해야 합니다.

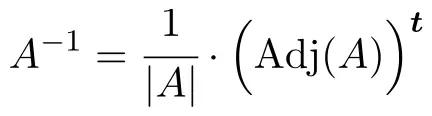
그러나 행렬식의 행렬식이 0이라면 이는 행렬이 가역적이지 않음을 의미합니다. 따라서 가장 먼저 해야 할 일은 행렬의 행렬식을 계산하고 그것이 0과 다른지 확인하는 것입니다.

$\displaystyle \lvert A \rvert = \begin{vmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{vmatrix} = -4- (-6) = 2$

행렬식은 0이 아니므 로 역행렬이 됩니다 .

따라서 행렬식의 값을 공식에 대입하면 행렬의 역행렬은 다음과 같습니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

$\displaystyle A^{-1} = \cfrac{1}{2} \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

이제 A의 부행렬을 계산해야 합니다. 이를 위해서는 행렬 A의 각 요소를 부행렬로 대체해야 합니다.

첨부 파일 을 계산하려면 다음을 기억하십시오.

$a_{ij}$

, 즉 행 요소에 대한 것입니다.

$i$

그리고 열

$j$

, 다음 공식을 적용해야 합니다.

$\text{Adjunto de } a_{ij} = (-1)^{i+j} \bm{\cdot} \text{Menor complementario de } a_{ij}$

보완적인 부전공

$a_{ij}$

행을 제거하는 행렬의 행렬식입니다.

$i$

그리고 열

$j$

따라서 행렬 A 요소의 대리인은 다음과 같습니다.

$\displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}$

$\text{Adjunto de 4} =\displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} -1 \end{vmatrix} = 1 \cdot (-1) = \bm{-1}$

$\text{Adjunto de -2} =\displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix} 3 \end{vmatrix} = -1 \cdot 3 = \bm{-3}$

$\text{Adjunto de 3} =\displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} -2 \end{vmatrix} = -1 \cdot (-2) = \bm{2}$

$\text{Adjunto de -1} =\displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 4 \end{vmatrix} = 1 \cdot 4 = \bm{4}$

설명: 행렬식 1×1을 절대값과 혼동하지 마십시오. 왜냐하면 행렬식 1×1에서는 숫자가 양수로 변환되지 않기 때문입니다.

대리인이 계산되면 A의 대리인 행렬을 찾기 위해 A의 요소를 대리인으로 대체하면 됩니다.

$\displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix}$

설명: 특정 위치에서 수반 행렬은 여기서 정의한 수반 행렬의 전치입니다.

따라서 첨부된 행렬을 역행렬 공식에 대체하면 다음과 같이 됩니다.

$\displaystyle A^{-1} = \cfrac{1}{2} \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

$\displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix} ^{\bm{t}}$

전시자

$\bm{t}$

이는 우리가 행렬을 전치 해야 함을 알려줍니다. 그리고 행렬을 전치하려면 행을 열로 변경 해야 합니다. 즉, 행렬의 첫 번째 행이 행렬의 첫 번째 열이 되고 두 번째 행이 두 번째 열이 됩니다.

$\displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & 2 \\[1.1ex] -3 & 4 \end{pmatrix}$

그리고 마지막으로 행렬의 각 항에 다음을 곱합니다.

$\cfrac{1}{2} :$

$\displaystyle A^{-1} = \begin{pmatrix} \sfrac{-1}{2} & \sfrac{2}{2} \\[1.1ex] \sfrac{-3}{2} & \sfrac{4}{2} \end{pmatrix}$

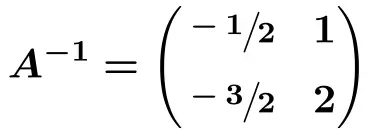
행렬식(또는 인접한 행렬) 방법을 사용하여 역행렬에 대한 연습 문제 해결

연습 1

수반 행렬 방법을 사용하여 다음과 같은 2×2 차원 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{pmatrix}$

솔루션 보기

역행렬 공식은 다음과 같습니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

먼저 행렬의 행렬식을 계산합니다.

$\displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{vmatrix} = 7-6 = 1$

행렬식은 0이 아니므로 행렬을 반전시킬 수 있습니다.

이제 A의 수반 행렬을 계산해 보겠습니다.

$\text{Adjunto de 1} =\displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 7 \end{vmatrix} = 1 \cdot 7 = \bm{7}$

$\text{Adjunto de 3} =\displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix} 2\end{vmatrix} = -1 \cdot 2 = \bm{-2}$

$\text{Adjunto de 2} =\displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3 \end{vmatrix} = -1 \cdot 3 = \bm{-3}$

$\text{Adjunto de 7} =\displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 \end{vmatrix} = 1 \cdot 1 = \bm{1}$

$\displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}$

행렬의 행렬식과 수반자가 계산되면 해당 값을 공식에 대체합니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

$\displaystyle A^{-1} = \cfrac{1}{1} \cdot \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}^{\bm{t}}$

첨부된 행렬을 전치합니다:

$\displaystyle A^{-1} = 1 \cdot \begin{pmatrix} 7 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}$

따라서 A의 역행렬은 다음과 같습니다.

$\displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{7} & \bm{-3} \\[1.1ex] \bm{-2} & \bm{1} \end{pmatrix}$

연습 2

행렬식 방법을 사용하여 다음 정사각 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} -3 & -2 \\[1.1ex] 5 & 4 \end{pmatrix}$

솔루션 보기

역행렬 공식은 다음과 같습니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

먼저 행렬의 행렬식을 계산합니다.

$\displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} -3 & -2 \\[1.1ex] 5 & 4\end{vmatrix} = -12+10 = -2$

행렬식은 0이 아니므로 행렬을 반전시킬 수 있습니다.

이제 A의 수반 행렬을 계산해 보겠습니다.

$\text{Adjunto de -3} =\displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4 \end{vmatrix} = 1 \cdot 4 = \bm{4}$

$\text{Adjunto de -2} =\displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix} 5\end{vmatrix} = -1 \cdot 5 = \bm{-5}$

$\text{Adjunto de 5} =\displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} -2 \end{vmatrix} = -1 \cdot (-2) = \bm{2}$

$\text{Adjunto de 4} =\displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} -3 \end{vmatrix} = 1 \cdot (-3) = \bm{-3}$

$\displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}$

행렬의 행렬식과 수반자를 찾으면 해당 값을 공식에 대체합니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

$\displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}^{\bm{t}}$

첨부된 행렬을 전치합니다:

$\displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] -5 & -3 \end{pmatrix}$

각 요소에 다음을 곱합니다.

$\cfrac{1}{-2} :$

$\displaystyle A^{-1} = \begin{pmatrix} \cfrac{4}{-2} & \cfrac{2}{-2} \\[3ex] \cfrac{-5}{-2} & \cfrac{-3}{-2} \end{pmatrix}$

따라서 A의 역행렬은 다음과 같습니다.

$\displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{-2} & \bm{-1} \\[2ex] \cfrac{\bm{5}}{\bm{2}} & \cfrac{\bm{3}}{\bm{2}} \end{pmatrix}$

연습 3

수반 행렬 방법을 사용하여 다음과 같은 3×3 차원 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}$

솔루션 보기

역행렬 공식은 다음과 같습니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

먼저 Sarrus 규칙을 사용하여 행렬의 행렬식을 해결합니다.

$\displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3 \end{vmatrix} = -24+6-2+16-2+9 = 3$

행렬식은 0이 아니므로 행렬을 반전시킬 수 있습니다.

행렬식을 풀면 A의 수반행렬을 찾을 수 있습니다.

$\text{Adjunto de 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}$

$\text{Adjunto de 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}$

$\text{Adjunto de -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}$

$\text{Adjunto de 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}$

$\text{Adjunto de 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}$

$\text{Adjunto de 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}$

$\text{Adjunto de 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}$

$\text{Adjunto de 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}$

$\text{Adjunto de -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}$

$\displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}$

행렬과 수반 행렬의 행렬식을 계산한 후 해당 값을 공식에 대체합니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

$\displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}^{\bm{t}}$

첨부된 행렬을 전치합니다:

$\displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}$

그리고 역행렬 A는 다음과 같습니다.

$\displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}$

연습 4

수반 행렬 방법을 사용하여 다음 차수 3 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}$

솔루션 보기

역행렬 공식은 다음과 같습니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

행렬식을 먼저 계산해야 합니다. 행렬식이 0이면 행렬에 역행렬이 없다는 의미이기 때문입니다.

$\displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1 \end{vmatrix} = 12+30+8+9-64+5 = \bm{0}$

A의 행렬식은 0이므로 행렬을 뒤집을 수 없습니다.

연습 5

다음 3 × 3 정방행렬을 행렬식 방법으로 반전시킵니다.

$\displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}$

솔루션 보기

역행렬 공식은 다음과 같습니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

먼저 우리는 Sarrus 규칙을 사용하여 행렬의 행렬식을 해결합니다.

$\displaystyle \lvert A \rvert = \begin{vmatrix} 1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2 \end{vmatrix} = 2+0-12-3-0+16 = 3$

행렬식은 0이 아니므로 행렬을 반전시킬 수 있습니다.

행렬식을 풀면 A의 수반행렬을 찾을 수 있습니다.

$\displaystyle \text{Adjunto de 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}$

$\displaystyle \text{Adjunto de 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}$

$\displaystyle \text{Adjunto de -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}$

$\displaystyle \text{Adjunto de -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}$

$\displaystyle \text{Adjunto de 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}$

$\displaystyle \text{Adjunto de 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}$

$\displaystyle \text{Adjunto de -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}$

$\displaystyle \text{Adjunto de -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}$

$\displaystyle \text{Adjunto de 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}$

$\displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}$

행렬과 수반 행렬의 행렬식을 계산한 후 해당 값을 공식에 대체합니다.

$\displaystyle A^{-1} = \cfrac{1}{\vert A \vert } \cdot \Bigl( \text{Adj}(A)\Bigr)^{\bm{t}}$

$\displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9\end{pmatrix}^{\bm{t}}$

첨부된 행렬을 전치합니다:

$\displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}$

그리고 마지막으로 우리는 다음을 운영합니다.

$\displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}$

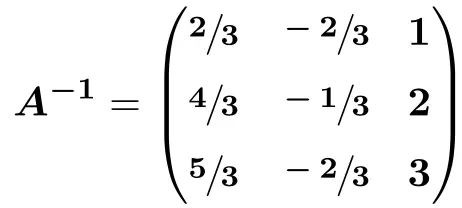
Gauss 방법을 사용하여 행렬을 반전시킵니다.

가우스 방법으로 행렬의 역함수를 계산 하려면 행렬의 행에 대해 연산을 수행해야 합니다 (이 내용은 나중에 살펴보겠습니다). 따라서 가우스 방법을 사용하는 방법을 알아보기 전에 행렬 행에서 수행할 수 있는 모든 작업을 아는 것이 중요합니다.

가우스 방법에서 허용되는 선 변환

행렬의 행 순서를 변경합니다 .

예를 들어, 행렬의 라인 2와 3의 순서를 변경할 수 있습니다.

$\left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] -2 & 4 & -1 \\[2ex] 6 & 1 & -3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] 6 & 1 & -3 \\[2ex] -2 & 4 & -1 \end{array} \right)$

행의 모든 항에 0이 아닌 숫자를 곱하거나 나눕니다 .

예를 들어, 라인 1을 4로 곱하고 라인 3을 2로 나눌 수 있습니다.

$\left( \begin{array}{ccc} 1 & -2 & 3 \\[2ex] 3 & -1 & 5 \\[2ex] 2 & -4 & -2 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc} 4 & -8 & 12 \\[2ex] 3 & -1 & 5 \\[2ex] 1 & -2 & -1 \end{array} \right)$

행을 동일한 행과 다른 행의 합에 숫자를 곱한 값으로 바꿉니다 .

예를 들어, 다음 행렬에서는 행 3에 1을 곱한 값을 행 2에 추가합니다.

$\left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 2 & 4 & 1 \\[2ex] 1 & -2 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1\cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 3 & 2 & 4 \\[2ex] 1 & -2 & 3 \end{array} \right)$

Gauss 방법을 사용하여 역행렬을 계산하는 예:

행렬을 반전시키기 위해 Gauss 방법을 적용하는 방법을 예를 통해 살펴보겠습니다.

다음 행렬의 역함수를 계산합니다.

$\displaystyle A = \left( \begin{array}{ccc} 1 & 0 & 1 \\[2ex] 0 & 2 & 1 \\[2ex] 1 & 5 & 4 \end{array} \right)$

가장 먼저 해야 할 일은 A 행렬과 단위 행렬을 하나의 행렬로 결합하는 것입니다. 왼쪽의 A 행렬과 오른쪽의 항등 행렬:

$\displaystyle \bigl( A \ \lvert \ I \bigr)$

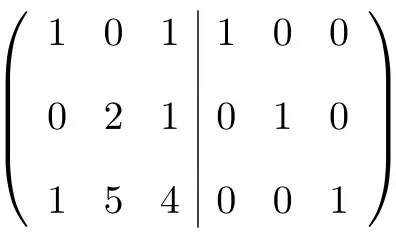
역행렬을 계산하려면 왼쪽 행렬을 단위 행렬로 변환해야 합니다. 그리고 그렇게 하려면 거기에 도달할 때까지 행에 변환을 적용해야 합니다.

즉, 행에 대한 작업을 수행하여 먼저 첫 번째 열의 숫자를 변환한 다음 두 번째 열의 숫자, 마지막으로 세 번째 열의 숫자를 변환합니다.

첫 번째 열의 1과 0은 이미 적합합니다. 단위 행렬의 위치에도 1과 0이 있기 때문입니다. 따라서 지금은 이러한 행에 변환을 적용할 필요가 없습니다.

$\left( \begin{array}{ccc|ccc} \color{blue}\boxed{\color{black}1} & 0 & 1 & 1 & 0 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right)$

그러나 단위 행렬의 첫 번째 열의 마지막 요소에는 0이 있고 이제 1이 있습니다. 따라서 1을 0으로 변환해야 합니다. 이렇게 하려면 행 1에 –를 곱한 값을 행 3.1에 추가합니다.

$\begin{array}{lrrr|rrr} & 1 & 5 & 4 &0 & 0 & 1 \\ + & -1 & 0 & -1 & -1 & 0 & 0 \\ \hline & 0 & 5 & 3 & -1 & 0 & 1 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_3} \\ \color{blue}\bm{\leftarrow -f_1} \\ \phantom{hline} \\ \end{array}$

따라서 이 합을 계산하면 다음 행렬이 됩니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 5 & 3 & -1 & 0 & 1 \end{array} \right)$

이로써 1을 0으로 바꾸는 데 성공했습니다.

이제 왼쪽 행렬의 두 번째 열로 이동하겠습니다. 첫 번째 요소는 0입니다. 이는 단위 행렬의 동일한 위치에 0이 있기 때문에 좋습니다. 그러나 2 대신 1이 있어야 하므로 두 번째 줄을 2로 나눕니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/2}\\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}1} & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right)$

또한 두 번째 열에서는 5를 0으로 바꿔야 합니다. 5는 두 번째 행의 1보다 5배 크기 때문에 행 2에 -5를 곱한 값을 행 3에 추가합니다.

$\begin{array}{lrrr|rrr} & 0 & 5 & 3 & -1 & 0 & 1 \\ + & 0 & -5 & \sfrac{-5}{2} & 0 & \vphantom{\Bigl(}\sfrac{-5}{2} & 0 \\ \hline & 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} \vphantom{\Bigl(} & 1 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_3} \\ \color{blue}\bm{\leftarrow -5f_2}\vphantom{\Bigl(} \\ \phantom{hline} \vphantom{\Bigl(} \end{array}$

따라서 이 작업을 수행하면 두 번째 열의 마지막 요소에 0이 있는 행렬이 생성됩니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 5f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)$

마지막으로 행렬의 마지막 열을 왼쪽으로 변환하지만 이번에는 아래쪽부터 시작해야 합니다. 그러므로 변환이 필요하다.

$\sfrac{1}{2}$

1로 바꿉니다. 따라서 마지막 줄에 2를 곱합니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \color{blue}\boxed{\color{black}1} & -2 & -5 & 2 \end{array} \right)$

이제 우리는 변화해야 한다.

$\sfrac{1}{2}$

마지막 열의 나머지 부분은 0입니다. 그러나 이번에는 행에 2를 곱할 수 없습니다. 왜냐하면 1을 2로 변환하기 때문입니다(단위 행렬의 해당 위치에 1이 있는 경우). 따라서 라인 3을 -2로 나눈 값을 라인 2에 추가합니다.

$\begin{array}{lrrr|rcr} & 0 & 1 & \vphantom{\Bigl(} \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\ + & 0 & 0 &\vphantom{\Bigl(} -\sfrac{1}{2} & 1 & \sfrac{5}{2} & -1 \\ \hline & 0 & 1 & 0\phantom{0} & 1 & 3 \vphantom{\Bigl(} & -1 \end{array} \begin{array}{l}\vphantom{\Bigl(} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_3/(-2)}\vphantom{\Bigl(} \\ \phantom{hline} \vphantom{\Bigl(} \end{array}$

따라서 이 작업을 수행함으로써 우리는

$\sfrac{1}{2}$

0에서:

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \color{blue}\boxed{\color{black}0} & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)$

마지막으로 세 번째 열의 첫 번째 행에 있는 1을 0으로 변환하면 됩니다. 세 번째 행에도 동일한 열에 1이 있으므로 행 3에 -1을 곱한 값을 행 1에 추가합니다.

$\begin{array}{lrrr|rcr} & 1 & 0 & 1 & 1 & 0 & 0 \\ + & 0 & 0 & -1 & 2 & 5 & -2 \\ \hline & 1 & 0 & 0 & 3 & 5 & -2 \end{array} \begin{array}{l}\color{blue}\bm{\leftarrow f_1} \\ \color{blue}\bm{\leftarrow -f_3}\\ \phantom{hline} \end{array}$

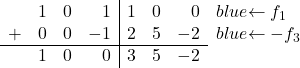
그리고 이 작업을 수행하여 1을 0으로 변환합니다.

$\ \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 &0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & \color{blue}\boxed{\color{black}0} & 3 & 5 & -2 \\[2ex] 0 & 1 & 0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)$

왼쪽 행렬을 단위 행렬로 성공적으로 변환하면 역행렬도 알게 됩니다. 역행렬은 왼쪽 행렬을 단위 행렬로 변환하여 오른쪽에서 얻는 행렬이기 때문입니다. 따라서 행렬의 역함수는 다음과 같습니다.

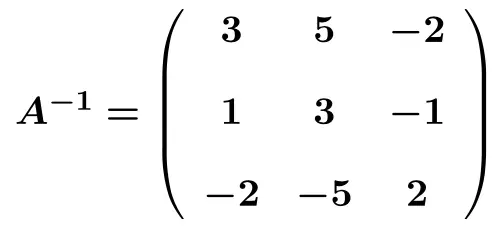
가우스 방법을 사용한 역행렬 연습 문제 해결

연습 1

Gauss 방법을 통해 다음 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] 1 & 3 \end{pmatrix}$

솔루션 보기

가장 먼저 해야 할 일은 A 행렬과 단위 행렬을 하나의 행렬로 결합하는 것입니다. 왼쪽의 A 행렬과 오른쪽의 단위 행렬:

$\displaystyle \left( A \ | \ I \right)$

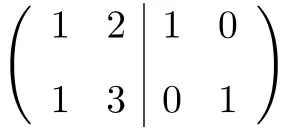
이제 역행렬을 계산하려면 왼쪽 행렬을 단위 행렬로 변환해야 합니다. 그리고 그렇게 하려면 거기에 도달할 때까지 행에 변환을 적용해야 합니다.

첫 번째 항인 1은 이미 단위 행렬과 동일합니다. 따라서 지금은 첫 번째 행에 변환을 적용할 필요가 없습니다.

그러나 단위 행렬의 첫 번째 열의 마지막 요소에는 0이 있고 이제 1이 있습니다. 따라서 1을 0으로 변환해야 합니다. 이렇게 하려면 행 2에서 행 1을 뺍니다.

$\left( \begin{array}{cc|cc}1 & 2 & 1 & 0 \\[1.5ex] 1 & 3 & 0 & 1\end{array} \right) \begin{array}{c} \\[1.5ex] \xrightarrow{f_2 - f_1} \end{array} \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1\end{array} \right)$

두 번째 열로 넘어갑니다. 아래 1이 좋습니다. 그러나 단위 행렬의 해당 위치에는 0이 있으므로 위의 2는 아닙니다. 따라서 2를 0으로 변환하려면 라인 1에서 라인 2와 2를 곱한 값을 뺍니다.

$\left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - 2f_2} \\[1.5ex] & \end{array} \left( \begin{array}{cc|cc} 1 & 0 & 3 & -2 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right)$

역행렬은 왼쪽 행렬을 단위행렬로 변환한 후 오른쪽에서 얻는 행렬입니다. 이제 우리는 왼쪽에 항등행렬을 얻었습니다. 따라서 역행렬은 다음과 같습니다.

$\bm{A^{-1}= \left(} \begin{array}{cc} \bm{3} & \bm{-2} \\[1.5ex] \bm{-1} & \bm{1} \end{array}\bm{ \right)}$

연습 2

가우스 절차를 사용하여 다음 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 1 & 1 & -4 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 0 & 1 & 1 \end{pmatrix}$

솔루션 보기

먼저 A 행렬과 단위 행렬을 단일 행렬에 넣습니다.

$\displaystyle \left( A \ | \ I \right)$

$\left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)$

이제 왼쪽 행렬을 단위 행렬로 변환할 때까지 행을 변환해야 합니다.

왼쪽 행렬의 첫 번째 열은 이미 단위 행렬의 첫 번째 열과 동일합니다. 따라서 해당 번호를 수정할 필요가 없습니다.

그러나 단위 행렬의 두 번째 열의 두 번째 요소에는 1이 있고 이제 3이 있습니다. 따라서 3을 1로 변환해야 합니다. 이렇게 하려면 라인 2에서 라인 3에 2를 곱한 값을 뺍니다.

$\left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & 4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)$

단위 행렬의 두 번째 열의 마지막 요소에는 0이 있고 이제 1이 있습니다. 따라서 1을 0으로 변환해야 합니다. 이를 위해 라인 3에서 라인 2를 뺍니다.

$\left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)$

단위 행렬의 두 번째 열의 첫 번째 요소에는 0이 있고 이제 1이 있습니다. 따라서 1을 0으로 변환해야 합니다. 이를 위해 라인 1에서 라인 2를 뺍니다.

$\left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)$

이제 우리가 해야 할 일은 -4를 0으로 변환하는 것뿐입니다. 이를 위해 라인 3에 4를 곱한 값을 라인 1에 추가합니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3\end{array} \right) \begin{array}{c} \xrightarrow{f_1 + 4f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -5 & 14 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)$

우리는 이미 왼쪽 변에서 단위 행렬을 얻었습니다. 따라서 역행렬은 다음과 같습니다.

$\bm{A^{-1}= \left( } \begin{array}{ccc} \bm{1} & \bm{-5} & \bm{14} \\[2ex] \bm{0} & \bm{1} & \bm{-2} \\[2ex] \bm{0} & \bm{-1 }& \bm{3} \end{array} \bm{ \right)}$

연습 3

가우스 방법을 사용하여 다음 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 1 & 2 & 1 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 2 & 0 & 3 \end{pmatrix}$

솔루션 보기

작업을 시작하기 전에 A 행렬과 단위 행렬을 단일 행렬에 넣어야 합니다.

$\displaystyle \left( A \ | \ I \right)$

$\left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right)$

이제 행에 대한 연산을 통해 왼쪽 행렬을 단위 행렬로 변환해야 합니다.

첫 번째 열의 처음 두 요소는 이미 단위 행렬의 요소와 동일합니다. 따라서 이 수치를 수정할 필요는 없습니다.

그러나 단위 행렬의 첫 번째 열의 세 번째 요소에는 0이 있고 이제 2가 있습니다. 따라서 2를 0으로 변환해야 합니다. 이렇게 하려면 3행에서 1행과 2를 곱한 값을 뺍니다.

$\left( \begin{array}{ccc|ccc}1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 2f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)$

단위 행렬의 두 번째 열의 첫 번째 요소에는 0이 있고 이제 2가 있습니다. 따라서 2를 0으로 변환해야 합니다. 이렇게 하려면 라인 1에서 라인 2에 2를 곱한 값을 뺍니다.

$\left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 -2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)$

단위 행렬의 두 번째 열의 마지막 요소에는 0이 있고 이제 -4가 있습니다. 따라서 -4를 0으로 변환해야 합니다. 이렇게 하려면 행 2에 4를 곱한 값을 행 3에 추가합니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 +4f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)$

이제 우리가 해야 할 일은 세 번째 열의 첫 번째 요소를 0으로 변환하는 것입니다. 이를 위해 라인 3에 -1을 곱한 값을 라인 1에 추가합니다.

$\left( \begin{array}{ccc|ccc}1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 3 & -6 & -1\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)$

우리는 왼쪽의 행렬이 단위 행렬이라는 것을 이미 깨달았습니다. 그래서 행렬의 역행렬은

$A$

동쪽:

$\bm{A^{-1}= \left( } \begin{array}{ccc} \bm{3} & \bm{-6} & \bm{-1} \\[2ex] \bm{0} & \bm{1} & \bm{0} \\[2ex] \bm{-2} & \bm{4}& \bm{1} \end{array} \bm{ \right)}$

연습 4

가우스 방법을 사용하여 다음 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 1 & -2 & 0 \\[1.1ex] 1 & 2 & 2 \\[1.1ex] 0 & 3 & 2 \end{pmatrix}$

솔루션 보기

가장 먼저 해야 할 일은 A 행렬과 항등 행렬을 단일 행렬로 결합하는 것입니다.

$\displaystyle \left( A \ | \ I \right)$

$\left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)$

이제 행 연산을 적용하여 왼쪽 행렬을 단위 행렬로 변환해야 합니다.

첫 번째 열의 첫 번째 요소는 이미 단위 행렬의 요소와 동일합니다. 따라서 이를 변경할 필요는 없습니다.

그러나 단위 행렬의 첫 번째 열의 두 번째 요소에는 0이 있고 이제 1이 있습니다. 따라서 1을 0으로 변환해야 합니다. 이렇게 하려면 라인 2에서 라인 1을 뺍니다.

$\left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)$

두 번째 열로 이동합니다. 먼저 두 번째 행을 4로 나누어 4를 1로 변환합니다.

$\left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/4} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)$

단위 행렬의 두 번째 열의 첫 번째 요소에는 0이 있고 이제 -2가 있습니다. 따라서 -2를 0으로 변환해야 합니다. 이를 위해 라인 2에 2를 곱한 라인 1을 추가합니다.

$\begin{array}{lrrr|rcr} & 1 & -2 & 0 & 1 & 0 & 0 \\ + & 0 & 2 & 1 & \vphantom{\Bigl(}\sfrac{-2}{4} & \sfrac{2}{4} & 0 \\ \hline & 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} \vphantom{\Bigl(}& 0 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_1} \\ \color{blue}\bm{\leftarrow 2f_2}\vphantom{\Bigl(} \\ \phantom{hline} \vphantom{\Bigl(} \end{array}$

$\left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \xrightarrow{f_1 +2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)$

단위 행렬의 두 번째 열의 마지막 요소에는 0이 있고 이제 3이 있습니다. 따라서 3을 0으로 변환해야 합니다. 이렇게 하려면 3행에서 2행과 3을 곱한 값을 뺍니다.

$\begin{array}{lrrr|crr} & 0 & 3 & 2 & 0 & 0\phantom{0} & 1 \\ + & 0 & -3 & \vphantom{\Bigl(}\sfrac{-6}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 0 \\ \hline & 0 & 0 & \vphantom{\Bigl(}\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_3} \\ \color{blue}\bm{\leftarrow -3f_2}\vphantom{\Bigl(} \\ \phantom{hline} \vphantom{\Bigl(} \end{array}$

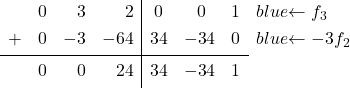
$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right)$

세 번째 열로 넘어갑니다. 마지막 열을 변환해야 합니다.

$\sfrac{2}{4}$

1로 바꿉니다. 이를 위해 세 번째 줄에 2를 곱합니다.

$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3 } \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)$

단위 행렬의 마지막 열의 두 번째 요소에는 0이 있습니다. 그러므로 변환이 필요하다.

$\sfrac{2}{4}$

0으로 변환합니다. 이렇게 하려면 2행에서 3행을 2로 나눈 값을 뺍니다.

$\begin{array}{lrrr|ccr} & 0 & 1 & \vphantom{\Bigl(} \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\ + & 0 & 0 & \vphantom{\Bigl(} \sfrac{-1}{2} & \sfrac{-6}{8} & \sfrac{6}{8} & -1 \\ \hline & 0 & 1 & 0\phantom{0} & -1 & 1 & -1\vphantom{\Bigl(} \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2}\vphantom{\Bigl(} \\ \color{blue}\bm{\leftarrow -f_3/2}\vphantom{\Bigl(} \\ \phantom{hline} \vphantom{\Bigl(} \end{array}$

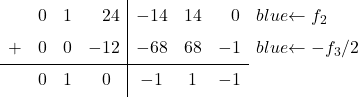
$\left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2 } \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)$

이제 우리가 해야 할 일은 세 번째 열의 첫 번째 요소를 0으로 변환하는 것입니다. 이를 위해 행 1에서 행 3을 뺍니다.

$\begin{array}{lrrr|rcr} & 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \vphantom{\Bigl(} \\ + & 0 & 0 & -1 & \sfrac{-6}{4} & \sfrac{6}{4} & -2 \vphantom{\Bigl(} \\ \hline & 1 & 0 & 0 & -1 & 2 & -2 \vphantom{\Bigl(} \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_1}\vphantom{\Bigl(} \\ \color{blue}\bm{\leftarrow -f_3}\vphantom{\Bigl(} \\ \phantom{hline} \vphantom{\Bigl(} \end{array}$

$\left( \begin{array}{ccc|ccc}1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3 } \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -1 & 2 & -2 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)$

따라서 역행렬은 다음과 같습니다.

$A^{-1}= \left( \begin{array}{ccc} -1 & 2 & -2 \\[2ex] -1 & 1 & -1 \\[2ex] \sfrac{6}{4} &\sfrac{-6}{4} & 2 \end{array} \bm{ \right)}$

마지막으로 역행렬의 분수는 다음과 같이 단순화될 수 있습니다.

$\bm{A^{-1}= \left( } \begin{array}{ccc} \bm{-1} & \bm{2} & \bm{-2} \\[2ex] \bm{-1} & \bm{1} & \bm{-1} \\[2ex] \sfrac{\bm{3}}{\bm{2}} &\sfrac{\bm{-3}}{\bm{2}} & \bm{2} \end{array} \bm{ \right)}$

역행렬 속성

역행렬은 다음과 같은 특징을 가지고 있습니다.

행렬의 역행렬은 고유 합니다.

역행렬의 역행렬은 원래 행렬입니다.

$\left(A^{-1}\right)^{-1} = A$

두 행렬의 곱셈의 역은 행렬의 역의 곱과 동일하지만 순서가 다릅니다.

$\left(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}$

행렬을 전치한 다음 역행렬을 수행하는 것은 먼저 행렬을 역전시킨 다음 이를 전치하는 것과 같습니다.

$\left(A^t\right)^{-1} = \left(A^{-1}\right)^{t}$

행렬의 역행렬의 행렬식을 풀기 위해 우리는 행렬의 행렬식을 계산한 다음 그 역행렬을 수행할 수 있습니다. 두 연산이 동일한 결과를 제공하기 때문입니다.

$\displaystyle det\left(A^{-1}\right) =\bigl( det(A) \bigr) ^{-1} = \cfrac{1}{det(A)}$

2×2 행렬의 역행렬을 빠르게 계산하는 공식

우리가 본 것처럼 모든 행렬은 행렬식이나 가우스 방법을 사용하여 역전될 수 있습니다. 그러나 별도로 2×2 행렬의 역행렬을 매우 빠르게 찾는 공식 도 있습니다.

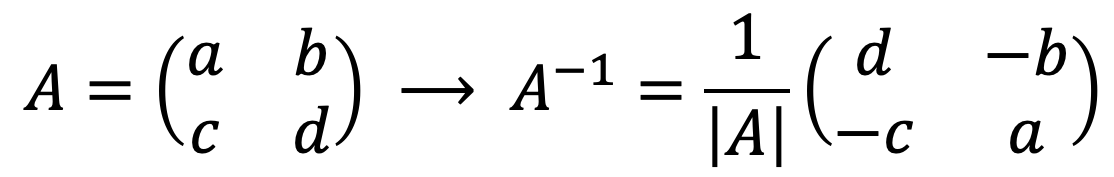
보시다시피, 2×2 행렬을 반전시키는 것은 간단합니다. 행렬식을 풀기만 하면 됩니다.

$(|A|)$

, 주대각선 요소의 위치를 교대로 바꾸고, 보조 대각선 요소의 부호를 변경합니다.

수식을 사용하여 2 × 2 역행렬을 얻는 방법의 예

다음 2 × 2 정사각 행렬의 역행렬을 계산합니다.

$\displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}$

행렬 A의 행렬식은 다음과 같습니다.

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}$

이제 역행렬 공식을 적용합니다.

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}$

그리고 행렬에 분수를 곱합니다.

$\displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}$

따라서 역행렬 A는 다음과 같습니다.

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}$

보시다시피, 이 공식을 사용하여 행렬을 반전시키는 것이 훨씬 빠르지만 2×2 차원의 행렬에만 사용할 수 있습니다.

공식을 사용하여 2×2 역행렬의 연습문제 해결

연습 1

2×2 차원의 다음 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}$

솔루션 보기

행렬 A의 행렬식은 다음과 같습니다.

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}$

이제 역행렬을 찾기 위해 공식을 적용합니다:

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}$

따라서 행렬 A의 역은 다음과 같습니다.

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}$

연습 2

다음 2차 행렬의 역행렬을 계산합니다.

$\displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}$

솔루션 보기

행렬 A의 행렬식은 다음과 같습니다.

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}$

이제 2×2 차원의 역행렬을 풀기 위해 공식을 적용합니다:

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}$

그리고 마지막으로 곱셈을 수행합니다.

$\displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}$

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}$

연습 3

다음 2×2 행렬을 반전시킵니다.

$\displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}$

솔루션 보기

행렬 A의 행렬식은 다음과 같습니다.

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}$

이제 2×2 차원의 역행렬을 계산하기 위해 공식을 적용합니다.

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}$

마지막으로 분수와 행렬 사이의 곱을 수행합니다.

$\displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}$

연습 4

다음 2차 행렬의 역행렬을 구합니다.

$\displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10 \end{pmatrix}$

솔루션 보기

행렬 A의 행렬식은 다음과 같습니다.

$\displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{vmatrix} & = (-2) \cdot 10- (-3) \cdot 5 \\ & = -20-(-15) \\[2ex] & =-20+15 \\[2ex] & =-5\end{aligned}$

이제 공식을 적용하여 2×2 차원의 역행렬을 생성합니다.

$\displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}$

$\displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{-5} \begin{pmatrix} 10 & -5 \\[1.1ex] 3 & -2 \end{pmatrix}$

그리고 마지막으로 곱셈을 수행합니다.

$\displaystyle A^{-1} = \begin{pmatrix} \cfrac{10}{-5} & \cfrac{-5}{-5} \\[3ex] \cfrac{3}{-5} & \cfrac{-2}{-5} \end{pmatrix}$

$\displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-2} & \bm{1} \\[2ex] \bm{-}\cfrac{\bm{3}}{\bm{5}} & \cfrac{\bm{2}}{\bm{5}} \ \end{pmatrix}$

역행렬을 사용하여 연립방정식 풀기

역행렬의 실제 적용을 평가하는 것은 어렵습니다. 사실, 아마도 궁금하실 겁니다… 역행렬은 어디에 사용되나요? 정말 어떤 용도로 사용되나요?

음, 역행렬의 용도 중 하나는 선형 방정식 시스템을 푸는 것 입니다. 그리고 그렇습니다. 비록 두 가지가 매우 다른 개념처럼 보일 수 있지만 행렬을 반전시켜 연립방정식에 대한 해를 찾는 것이 가능합니다.

이것이 어떻게 수행되는지 예를 통해 살펴보겠습니다.

역행렬을 사용하여 다음 방정식 시스템의 해를 계산합니다.

$\left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}$

우선, 방정식 시스템이 행렬의 형태로 표현될 수 있다는 점을 관찰해야 합니다.

$\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}$

우리는 시스템의 이 행렬 형식이 방정식을 사용한 표현식과 동일하다는 것을 확인할 수 있습니다. 행렬을 곱하면 시스템의 두 방정식을 얻는다는 것을 알 수 있습니다.

이제 다음 단계를 단순화하기 위해 다음을 호출하겠습니다.

$A$

미지수의 계수를 갖는 행렬에,

$X$

미지수가 있는 행렬 열에

$B$

독립항을 갖는 열 행렬로:

$\displaystyle AX=B$

그래서 매트릭스

$X$

는 행렬 방정식의 미지수입니다.

이 행렬 방정식을 풀려면 여기서는 자세히 설명하지 않는 절차를 따라야 합니다. 완전히 이해하고 싶다면 행렬로 방정식을 푸는 방법을 확인해 보세요. 여기에서 전체 과정을 단계별로 설명합니다.

이 절차는 역행렬의 속성을 기반으로 합니다. 즉, 역행렬을 곱한 행렬은 항등(또는 단위) 행렬과 같습니다. 따라서 미지의 행렬은 쉽게 풀 수 있다.

$X$

방정식의 양변에 행렬 A의 역함수를 곱하면 다음과 같습니다.

$\displaystyle AX=B$

$\displaystyle A^{-1}\cdot AX=A^{-1}\cdot B$

$\displaystyle IX=A^{-1}\cdot B$

$\displaystyle X=A^{-1}\cdot B$

그리고 매트릭스를 분리한 후에는

$X$

, 우리는

$A$

그리고 우리는 행렬의 곱을 푼다:

$\displaystyle X=\left.\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\right.^{-1}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}$

$\displaystyle X=\cfrac{1}{-2} \begin{pmatrix} 4 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}$

$\displaystyle X= \begin{pmatrix} -1 \\[1.1ex] 2 \end{pmatrix}$

따라서 연립방정식의 해는 다음과 같습니다.

$\displaystyle \bm{x=-1} \qquad \bm{y=2}$

행렬의 역행렬은 무엇입니까?

언제 행렬을 반전할 수 있고 언제 반전할 수 없나요?

행렬식 방법을 사용하여(또는 인접 행렬을 사용하여) 행렬 반전

행렬식 방법(또는 수반 행렬)을 사용하여 역행렬을 계산하는 예:

행렬식(또는 인접한 행렬) 방법을 사용하여 역행렬에 대한 연습 문제 해결

연습 1

연습 2

연습 3

연습 4

연습 5

Gauss 방법을 사용하여 행렬을 반전시킵니다.

가우스 방법에서 허용되는 선 변환

Gauss 방법을 사용하여 역행렬을 계산하는 예:

가우스 방법을 사용한 역행렬 연습 문제 해결

연습 1

연습 2

연습 3

연습 4

역행렬 속성

2×2 행렬의 역행렬을 빠르게 계산하는 공식

수식을 사용하여 2 × 2 역행렬을 얻는 방법의 예

공식을 사용하여 2×2 역행렬의 연습문제 해결

연습 1

연습 2

연습 3

연습 4

역행렬을 사용하여 연립방정식 풀기

댓글 달기 댓글 취소