여기서는 함수의 오목함과 볼록함이 무엇인지, 그리고 함수가 오목함인지 볼록함인지 구별하는 방법을 배웁니다. 또한 함수의 곡률에 대한 단계별 연습을 통해 연습할 수 있습니다.
함수의 오목함과 볼록함은 무엇입니까?
함수의 오목함과 볼록함은 함수 그래프의 곡률을 나타냅니다. 그래프가 산 모양인 함수를 오목 함수, 계곡 모양을 한 함수를 볼록 함수라고 합니다.
앞 문단에서는 이해의 편의를 위해 오목함수와 볼록함수를 비공식적으로 정의했지만, 오목함수와 볼록함수의 수학적 정의는 다음과 같습니다.
- 오목 함수(Concave function): 함수의 두 점을 연결하는 선분이 곡선 아래에 있는 경우.
- 볼록함수(Convex function): 함수의 두 점을 연결하는 선분이 곡선 위에 있는 경우.
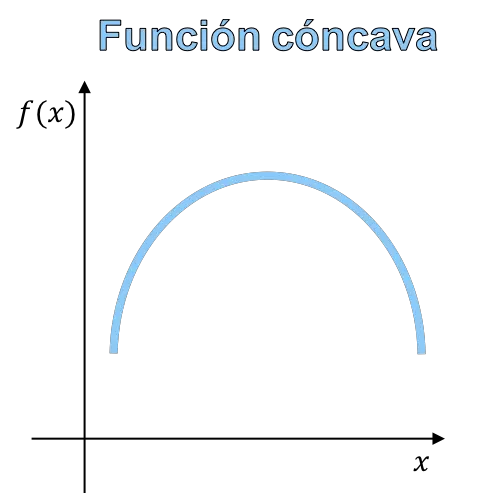

결국 오목함수와 볼록함수의 차이는 함수의 모양에 달려 있기 때문에 함수의 그래프를 보면 오목함수와 볼록함수를 구분할 수 있습니다.
그러나 함수가 반드시 전체 영역에 걸쳐 오목하거나 볼록할 필요는 없지만, 한 구간에서는 오목하고 다른 구간에서는 볼록할 수도 있습니다.
참고: 수학계에서는 여전히 완전히 동의하지 않기 때문에 일부 교수들은 그 반대라고 말합니다. 그들은 함수를 오목 함수라고 부릅니다.
![]()
, 그리고 다음과 같은 형태의 볼록 함수
![]()
. 어쨌든 중요한 것은 이름이 무엇이든 그 기능이 무엇인지 아는 것입니다.
함수의 곡률을 연구하는 방법
함수의 곡률을 연구한다는 것은 함수의 오목함과 볼록함을 찾는 것, 즉 함수가 오목한 간격과 함수가 볼록한 간격을 아는 것을 포함합니다.
따라서 함수의 곡률을 연구하려면 다음 단계를 수행해야 합니다.
- 함수의 정의역에 속하지 않는 점을 찾습니다.
- 함수의 1차 도함수와 2차 도함수를 계산합니다.
- 2차 도함수의 근을 구합니다. 즉, 다음을 풀어 2차 도함수를 상쇄하는 점을 계산합니다.
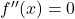
.
- 도함수의 근과 함수의 정의역에 속하지 않는 점으로 구간을 만듭니다.
- 각 구간의 한 지점에서 2차 도함수 값을 계산합니다.
- 따라서 2차 도함수의 부호는 이 구간에서 함수의 오목함이나 볼록함을 결정합니다.
- 함수의 2차 도함수가 양수이면 함수는 이 구간에서 볼록합니다 .
- 함수의 2차 도함수가 음수이면 함수는 이 구간에서 오목합니다 .
함수의 곡률을 찾는 방법의 예
다음으로, 함수의 오목 및 볼록 간격이 어떻게 계산되는지 확인할 수 있도록 단계별로 예제를 풀어보겠습니다.
- 다음 함수의 오목함과 볼록함을 연구합니다.
![]()
가장 먼저 해야 할 일은 함수의 정의 영역을 계산하는 것입니다. 이 경우 다항식 함수가 있으므로 함수의 정의역은 실수로 구성됩니다.
![]()
함수의 영역을 계산한 후에는 함수의 2차 도함수가 사라지는 지점을 조사해야 합니다.
따라서 우리는 함수의 1차 도함수를 계산합니다.
![]()
그런 다음 함수의 2차 도함수를 찾습니다.
![]()
이제 2차 도함수를 0으로 설정하고 방정식을 풉니다.
![]()
![]()
![]()
![]()
일단 함수의 도메인을 계산하고
![]()
, 우리는 선에서 발견된 모든 중요한 점을 나타냅니다. 이 경우 함수 정의 영역 계산에서 중요한 점을 찾지 못했지만 함수의 2차 도함수를 취소하는 점을 얻었습니다.
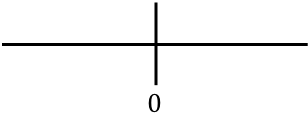
이제 각 간격에서 2차 도함수의 부호를 평가하여 함수가 오목인지 볼록인지 확인합니다. 따라서 우리는 각 간격(중요점이 아님)에서 점을 취하고 이 점에서 2차 도함수의 부호가 무엇인지 살펴봅니다.
![]()
![]()
![]()

마지막으로 함수의 오목함과 볼록함 간격을 추론합니다. 2차 도함수가 양수이면 함수가 볼록함을 의미합니다.
![]()
, 그리고 2차 도함수가 음수이면 이는 함수가 오목함을 의미합니다.
![]()
. 따라서 함수의 오목 및 볼록 간격은 다음과 같습니다.
볼록한
![]()
:
![]()
오목한
![]()
:
![]()
함수의 오목함과 볼록함에 대한 연습문제 해결
연습 1
다음 다항식 함수의 오목함과 볼록함 간격을 계산합니다.
![]()
연습의 함수는 다항식이므로 함수의 정의역은 실수로 구성됩니다.
![]()
함수의 영역을 결정한 후 이를 차별화합니다.
![]()
그런 다음 함수의 2차 도함수를 찾습니다.
![]()
이제 2차 도함수를 0으로 설정하고 방정식을 풉니다.
![]()
![]()
![]()
![]()
![]()
함수의 정의역을 계산하고 풀면
![]()
, 수직선에서 발견된 모든 특이점을 나타냅니다.

이제 각 간격에 속하는 점을 취하고 이 점에서 어떤 기호가 2차 도함수를 갖는지 살펴보겠습니다.
![]()
![]()

2차 도함수가 0보다 크면 함수가 볼록함을 의미합니다.
![]()
, 그러나 2차 도함수가 음수인 경우 이는 함수가 오목함을 의미합니다.
![]()
. 따라서 오목함과 볼록함의 간격은 다음과 같습니다.
볼록한
![]()
:
![]()
오목한
![]()
:
![]()
연습 2
다음 유리 함수의 곡률을 연구합니다.
![]()
먼저 함수의 정의역을 계산해야 합니다. 이것은 유리함수이므로 분모를 0으로 설정하여 어떤 숫자가 함수의 정의역에 속하지 않는지 확인합니다.
![]()
![]()
![]()
![]()
이는 x가 -2 또는 +2일 때 분모가 0이 된다는 것을 의미합니다. 따라서 함수는 존재하지 않습니다. 따라서 함수의 정의역은 x=-2와 x=+2를 제외한 모든 숫자로 구성됩니다.
![]()
둘째, 함수의 1차 도함수를 계산합니다.
![]()
![]()
그리고 나서 우리는 이차 도함수를 푼다:


모든 항에 다음을 곱합니다.
![]()
. 따라서 분수를 단순화할 수 있습니다.

![]()
![]()
![]()
![]()
이제 함수의 2차 도함수 근을 계산해 보겠습니다.
![]()
![]()
용어
![]()
여기에는 전체 왼쪽을 나누는 작업이 포함되므로 전체 오른쪽을 곱할 수 있습니다.
![]()
![]()
공통 요소를 추출합니다.
![]()
곱셈이 0이 되려면 곱셈의 두 요소 중 하나가 0이어야 합니다. 따라서 각 요소를 0으로 설정합니다.
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
실수에는 음의 근이 없기 때문에 해결책이 없습니다.
이제 얻은 모든 임계점, 즉 영역에 속하지 않는 점(x=-2 및 x=+2)과 2차 도함수를 취소하는 점(x=0)을 선에 나타냅니다.

그리고 각 간격에서 2차 도함수의 부호를 평가하여 함수가 오목인지 볼록인지 확인합니다. 따라서 우리는 각 구간의 한 점을 취하고 그 점에서 어떤 부호가 2차 도함수를 갖는지 살펴봅니다.
![]()
![]()
![]()
![]()

2차 도함수가 양수이면 함수가 볼록함을 의미합니다.
![]()
, 그리고 2차 도함수가 음수이면 이는 함수가 오목함을 의미합니다.
![]()
. 따라서 오목 및 볼록 간격은 다음과 같습니다.
볼록한
![]()
:
![]()
오목한
![]()
:
![]()
연습 3
기능
![]()
상대적으로 극단적인 면이 있다
![]()
. 게다가 함수는 볼록합니다.
![]()
이 시점에서. 상대적 극단값이 최소값인지 최대값인지 확인합니다.
➤ 참고: 함수의 최대값과 최소값 정의
볼록함수를 보자
![]()
~ 안에
![]()
이는 이 지점의 2차 도함수가 양수라는 것을 의미합니다. 즉
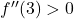 그러므로 상대적 극단은
그러므로 상대적 극단은
![]()
이는 최소값 이므로
![]()
긍정적입니다.