이 기사에서는 함수의 미분 가능성, 즉 함수가 미분 가능한지 여부를 연구하는 방법을 배우게 됩니다. 추가적으로, 우리는 함수의 미분성과 연속성 사이의 관계를 살펴볼 것입니다. 그리고 마지막으로, 조각별 함수의 미분가능성을 연구하겠습니다.
함수의 미분성과 연속성
한 점에서 함수의 연속성과 미분성은 다음과 같이 관련됩니다.
- 함수가 한 점에서 미분 가능하면 그 점에서 함수는 연속입니다.
- 함수가 한 점에서 연속적이지 않으면 그 점에서도 미분 가능하지 않습니다.
그러나 이 정리의 역은 거짓입니다. 함수가 한 점에서 연속이라고 해서 그 점에서 항상 미분 가능하다는 의미는 아닙니다.
또한 함수가 그래픽 표현의 한 지점에서 미분 가능한지 여부도 확인할 수 있습니다.
- 평활점 이라면 이 지점에서 함수가 미분 가능합니다.
- 각점 인 경우 함수는 연속이지만 이 지점에서는 미분할 수 없습니다.
x=0에서의 평활점 :
이 단계에서는 연속적이고 미분 가능한 함수입니다.
x=2의 각도점 :
함수는 연속이지만 이 단계에서는 미분할 수 없습니다.
조각별 함수의 미분성
함수의 연속성과 미분 가능성 사이의 관계를 알게 되면, 조각별로 정의된 함수의 미분 가능성을 연구하는 방법을 살펴보겠습니다.
해당 지점에서 측면 도함수를 계산하여 해당 지점에서 조각별 함수가 미분 가능한지 여부를 알 수 있습니다.
- 한 점의 측면 도함수가 동일하지 않으면 해당 점에서 함수를 미분할 수 없습니다.
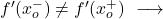
에서는 공제되지 않습니다.
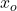
- 한 점에서 측면 도함수가 일치하면 함수는 해당 점에서 미분 가능합니다.
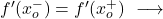
네, 구별 가능합니다
참고: 함수가 한 점에서 미분 가능하려면 함수가 해당 점에서 연속이어야 합니다. 따라서 측면 도함수를 계산하기 전에 함수가 해당 지점에서 연속인지 확인해야 합니다. 한 지점에서 연속성이 어떻게 연구되는지 모르는 경우 다음 링크에서 연속성이 어떻게 수행되는지 확인할 수 있습니다.
➤ 참조: 한 지점에서 함수의 연속성
이제 한 점에서 조각별로 정의된 함수의 도함수를 계산하는 방법의 예를 살펴보겠습니다.
- x=2 지점에서 조각별로 정의된 다음 함수의 연속성과 미분성을 연구합니다.
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
두 부분의 함수는 각각의 구간에서 연속이지만 임계점 x=2에서 함수가 연속인지 확인하는 것이 필요합니다. 이를 위해 다음 지점에서 함수의 측면 한계를 해결합니다.
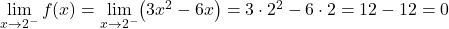
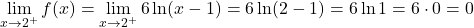
임계점의 측면 한계는 동일한 결과를 제공하므로 함수는 x=2 지점에서 연속입니다.
함수가 x=2에서 연속이라는 것을 알게 되면, 그 지점에서 함수의 미분 가능성을 연구할 것입니다. 이를 위해 조각으로 정의된 함수의 측면 도함수를 계산합니다 .
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
이제 임계점에서 각 측면 파생 상품을 평가합니다.
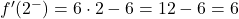
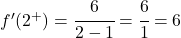
두 개의 측면 도함수는 동일한 결과를 제공하므로 함수는 x=2에서 미분 가능하고 도함수의 값은 6입니다.
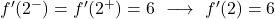
반면, 측면 도함수가 우리에게 다른 결과를 제공했다면 이는 함수가 x=2에서 미분 가능하지 않음을 의미합니다. 즉, 이 시점에서는 파생 상품이 존재하지 않습니다.
마지막으로, 절대값 함수는 조각별로 정의될 수 있으므로 이 절차는 절대값 함수의 미분 가능성을 연구하는 데에도 유효하다는 점을 기억하세요. 여기에서 절대값 함수를 청크로 변환하는 방법을 볼 수 있습니다.
➤ 참고: 절대값을 사용하여 함수를 조각별로 정의하는 방법
함수의 미분 가능성에 대한 해결 연습
연습 1
다음 조각별 함수의 연속성과 미분성을 연구합니다.
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
두 부분의 함수는 연속이지만 임계점 x=1에서 함수가 연속인지 확인해야 합니다. 이를 위해 우리는 해당 지점에서 함수의 측면 한계를 해결합니다.
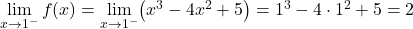
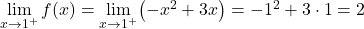
임계점의 두 측면 극한은 동일한 결과를 제공하므로 함수는 x=1에서 연속입니다.
함수가 임계점에서 연속이라는 것을 알게 되면, 같은 점에서 미분이 가능한지 연구해 보겠습니다. 따라서 우리는 측면 파생 상품을 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
그리고 우리는 x=1에서 두 개의 측면 도함수를 평가합니다.
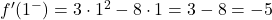
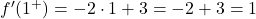
측면 도함수는 x=1 지점에서 일치하지 않으므로 이 지점에서는 함수를 미분할 수 없습니다.
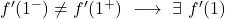
연습 2
섹션에 정의된 다음 함수의 미분성과 연속성을 분석합니다.
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
솔루션 보기
두 부분의 함수는 간격에 따라 연속적이지만 정의 x=1의 변화 임계점에서 함수가 연속적인지 여부도 알아야 합니다. 따라서 우리는 이 시점에서 함수의 측면 한계를 정의합니다.
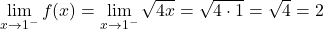
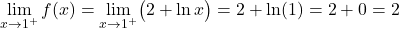
임계점의 두 측면 극한은 동일한 결과를 제공하므로 함수는 x=1에서 연속입니다.
이제 측면 도함수를 계산하여 이 시점에서 함수가 미분 가능한지 연구합니다.
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
x=1에서 두 개의 측면 도함수를 평가합니다.
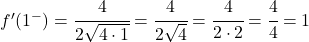
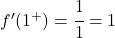
측면 도함수는 동일하므로 함수는 x=1에서 미분 가능하고 도함수 값은 1입니다.
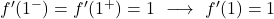
연습 3
다음 조각별 함수가 전체 영역에 걸쳐 연속적이고 미분 가능한지 여부를 확인합니다.
*** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+1 & \text{si} & x\leq -1 \\[2ex] 2x+2 & \text{ si} & -1<div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E6F9EF" role="button" tabindex="0" aria- expanded="false" data-otfm-spc="#E6F9EF" style="text-align:center"><div class="otfm-sp__title"> <strong>View solution</strong></div>< /div> The functions of all three parts are continuous, but we still need to check if the function is continuous at critical points. We therefore first check the continuity of the function at the point x=-1 by solving the lateral limits at this point:
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: ...="wp-block-otfm-box-spoiler-start otfm-sp__
Missing { inserted.
leading text: ...ox-spoiler-start otfm-sp__wrapper otfm-sp__
Missing { inserted.
leading text: ...m-sp__wrapper otfm-sp__box js-otfm-sp-box__
Missing { inserted.
leading text: ...fm-sp__box js-otfm-sp-box__closed otfm-sp__
You can't use `macro parameter character #' in math mode.
leading text: ...="0" aria-expanded="false" data-otfm-spc="#
Missing { inserted.
leading text: ...e="text-align:center"><div class="otfm-sp__
Please use \mathaccent for accents in math mode.
leading text: ...g></div></div> The functions of the three parts
Please use \mathaccent for accents in math mode.
leading text: ...are continuous, but we still need to see
\lim\limits_{x\to -1^-} f(x) = \lim\limits_{x\to -1^-} \bigl(x^2+2x+1\bigr) = (-1)^ 2+2(-1)+1 =0 \lim\limits_{x\to -1^+} f(x) = \lim\limits_{x\to -1^+} \bigl(2x+2\bigr ) = 2(-1)+2=0
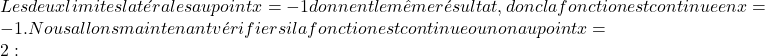
\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(2x+2\bigr) = 2\cdot 2+2=4+2= 6 \lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} \bigl( -x^2+8x\bigr) = -2^2+8\ cdot 2 = -4+16=12
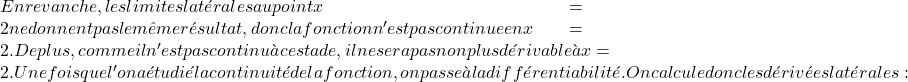
\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2x+2 & \text{si} & x\leq -1 \\[2ex] 2 & \text{si} & -1
우리는 함수가 x=2에서 미분 가능하지 않다는 것을 이미 알고 있으므로 x=-1에서 함수가 미분 가능한지 연구하면 됩니다. 이를 위해 우리는 해당 지점에서 두 개의 측면 파생 상품을 평가합니다.
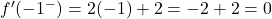
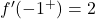
측면 도함수는 x=-1 지점에서 일치하지 않으므로 해당 지점에서 함수를 미분할 수 없습니다.
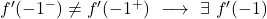
연습 4
다음 조각별 함수가 해당 영역 전체에서 연속적이고 미분 가능하도록 매개변수 a와 b의 값을 계산합니다.
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
미지수의 값이 무엇이든, 함수는 연속성과 미분 가능성을 확인해야 하는 x=3을 제외한 모든 지점에서 연속적이고 미분 가능합니다.
함수가 한 점에서 연속이 되려면 해당 점의 두 측면 극한이 일치해야 합니다. 따라서 우리는 임계점에서 측면 한계를 평가합니다.
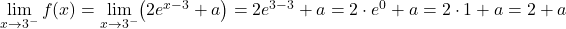
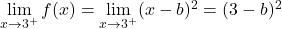
따라서 함수가 연속되려면 측면 한계에서 얻은 두 값이 동일해야 합니다.
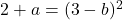
이제 x=3 지점에서 미분가능성을 분석하겠습니다. 우리는 측면 파생 상품을 찾습니다.
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)
그리고 우리는 임계점에서 두 개의 측면 파생 상품을 평가합니다.
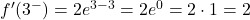
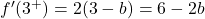
따라서 함수가 x=3에서 미분 가능하려면 측면 도함수에서 얻은 값이 동일해야 합니다.
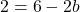
그리고 이 방정식을 풀면 b 값을 찾을 수 있습니다.
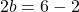
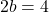
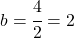
마지막으로 매개변수 b의 값을 알면 이전에 측면 한계에서 얻은 방정식을 풀어 매개변수 a의 값을 계산할 수 있습니다.
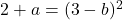
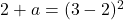
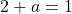
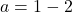
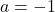


![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
![]()
![]()
![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
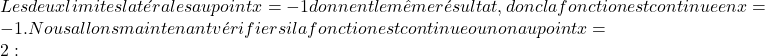
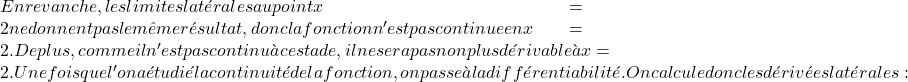
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)