쌍곡선 코탄젠트의 미분

여기에서는 함수의 쌍곡선 코탄젠트를 유도하는 방법을 설명합니다. 쌍곡선 코탄젠트의 도함수 예도 찾을 수 있습니다.

쌍곡선 코탄젠트의 도함수에 대한 공식

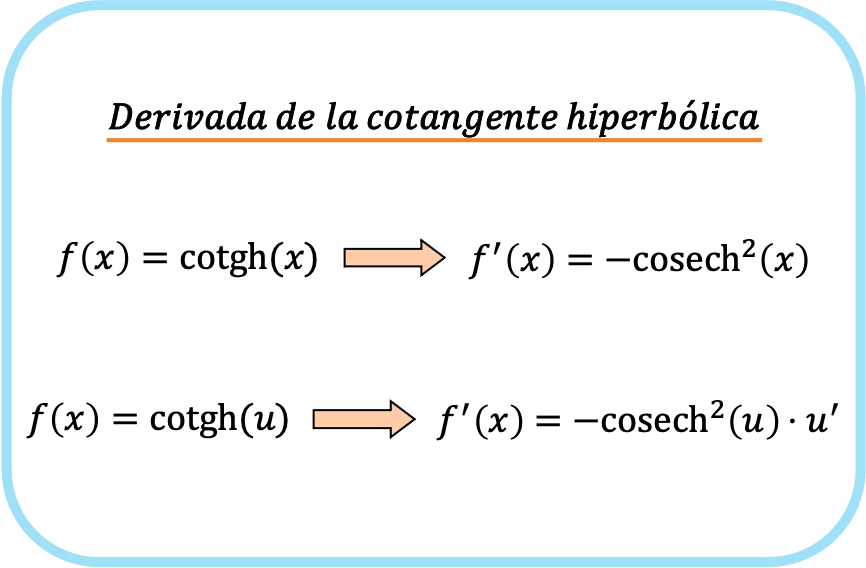
x의 쌍곡선 코탄젠트의 도함수는 x 제곱의 쌍곡선 코시컨트를 뺀 값과 같습니다.

$f(x)=\text{cotgh}(x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(x)$

그러므로, 함수의 쌍곡코탄젠트의 도함수는 함수의 쌍곡코시컨트를 빼고 그 함수의 도함수를 곱한 것입니다.

$f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'$

두 번째 수식에서는 체인 규칙이 적용되었으며 쌍곡선 코탄젠트 인수에 x 이외의 함수가 있을 때 이 수식이 사용된다는 점을 명심하세요.

일부 수학 서적에서는 코탄젠트의 도함수가 또 다른 것임을 알 수 있습니다. 다음 세 가지 표현은 동일하기 때문입니다.

$f'(x)=-\text{cosech}^2(x)=1-\text{cotgh}^2(x)=-\cfrac{1}{\text{senh}^2(x)}$

분명히, 쌍곡선 코탄젠트를 유도하기 위해 세 가지 중 원하는 표현을 사용할 수 있지만 가장 많이 사용되는 것은 쌍곡선 코시컨트 제곱입니다.

함수의 쌍곡선 코탄젠트 도함수 공식이 무엇인지 알게 되면 이러한 유형의 삼각함수 도함수에 대한 몇 가지 예를 풀 것입니다.

이 예에서 우리는 함수 2x의 쌍곡선 코탄젠트의 도함수가 무엇인지 볼 것입니다.

$f(x)=\text{cotgh}(2x)$

쌍곡선 코탄젠트 인수에는 x 이외의 함수가 있으므로 파생을 수행하려면 체인 규칙이 있는 공식을 사용해야 합니다.

$f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'$

2x는 1차 항이므로 그 도함수는 2입니다. 따라서 2x의 쌍곡선 코탄젠트의 도함수를 찾으려면 쌍곡코시컨트의 제곱 인수에 2x를 넣고 2를 곱하면 됩니다.

$f(x)=\text{cotgh}(2x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(2x)\cdot 2$

두 번째 예에서는 다항식 함수의 쌍곡코탄젠트 도함수 값을 결정합니다.

$f(x)=\text{cotgh}(3x^4-5x)$

위에서 본 것처럼, 함수의 쌍곡선 코탄젠트를 도출하는 규칙은 다음과 같습니다.

$f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'$

따라서 이 연습의 쌍곡선 코탄젠트의 미분은 다음과 같습니다.

$f(x)=\text{cotgh}(3x^4-5x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(3x^4-5x)\cdot(12x^3-5)$