여기에서 쌍곡선 아크사인(공식)의 파생물이 무엇인지 찾을 수 있습니다. 또한, 함수의 쌍곡선 아크사인 도함수에 대해 해결된 여러 연습 문제를 볼 수 있습니다. 마지막으로 이러한 유형의 삼각 함수의 미분 공식을 보여줍니다.
쌍곡선 아크사인 파생 공식
x의 쌍곡선 아크사인의 도함수는 x 제곱의 제곱근에 1을 더한 값입니다.
![]()
따라서 함수의 쌍곡선 아크사인의 도함수는 해당 함수의 도함수를 해당 함수의 제곱근에 1을 더한 값으로 나눈 몫과 같습니다.
![]()
두 번째 공식은 첫 번째 공식과 같지만 체인 규칙을 적용합니다. 즉, 첫 번째 공식을 사용하면 xy의 쌍곡선 아크사인만 유도할 수 있는 반면, 두 번째 공식을 사용하면 모든 함수의 쌍곡선 아크사인을 유도할 수 있습니다.

쌍곡선 아크사인은 쌍곡선 사인의 역함수이며, 그 파생 함수는 여기에서 볼 수 있습니다.
➤ 참조: 쌍곡사인의 도함수 공식
쌍곡선 아크사인 파생물의 예
실시예 1
![]()
아크사인 함수의 미분을 풀기 위해 위에 표시된 공식을 사용합니다.
![]()
3x의 도함수는 3이므로 분자에 3이 들어갑니다. 그리고 분모에는 3x 제곱 + 1의 제곱근을 넣으면 됩니다.
![]()
실시예 2
![]()
함수 x 세제곱의 쌍곡선 아크사인을 파생하려면 동일한 공식을 적용해야 합니다.
![]()
x 세제곱의 도함수는 3x 2 이므로 x를 3으로 올린 쌍곡선 아크사인의 도함수는 다음과 같습니다.
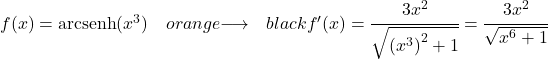
쌍곡선 아크사인 파생물의 증명
우리는 쌍곡선 아크사인의 미분에 대한 공식을 보여줄 것입니다:
![]()
먼저 쌍곡선 아크사인을 쌍곡선 사인으로 변환합니다.
![]()
우리는 평등의 양쪽 측면에서 추론합니다.
![]()
우리는 당신을 정리합니다:
![]()
그런 다음 쌍곡선 사인과 쌍곡선 코사인을 연결하는 삼각법 항등식을 적용합니다.
![]()
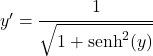
그러나 위에서 우리는 x가 y의 쌍곡사인에 해당한다고 추론했으므로 방정식은 그대로 유지됩니다.
![]()
보시다시피, 이러한 단계를 적용하여 쌍곡선 아크사인의 도함수에 대한 공식을 얻었으며 이것이 입증된 이유입니다.
유사한 항목
- 쌍곡선 시컨트의 도함수에 대한 공식
- Arcsecant 파생 공식
- 시컨트 미분 공식
- 아크사인 파생 공식
- 정현파 미분 공식