이 글에서는 함수의 아크사인을 유도하는 방법을 설명합니다. 함수의 아크사인 도함수의 예를 찾을 수 있으며 단계별로 연습문제를 풀어 연습할 수도 있습니다. 마지막으로 아크사인 파생 공식의 시연도 볼 수 있습니다.
아크사인의 미분은 무엇입니까?
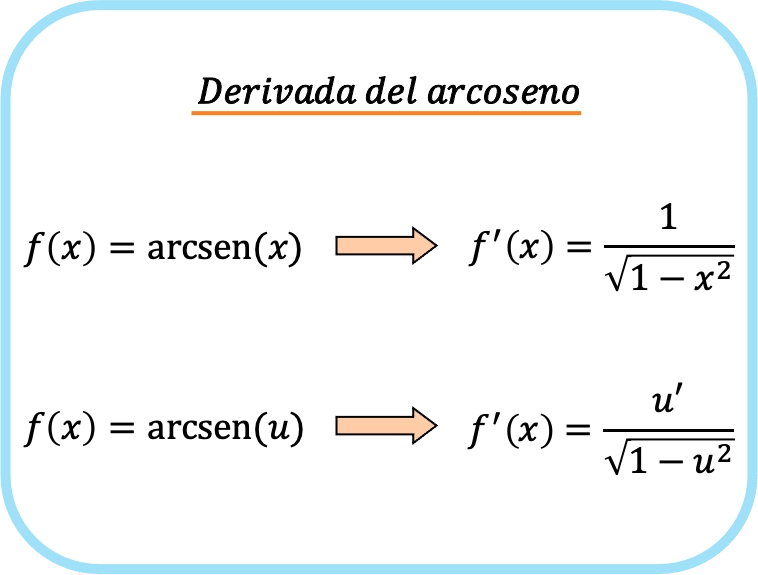
x의 아크사인 도함수는 1 – x 제곱의 제곱근 나누기 1입니다.
![]()
따라서 함수의 아크사인 도함수는 해당 함수의 도함수를 1의 제곱근에서 제곱 함수를 뺀 값으로 나눈 몫과 같습니다.
![]()
논리적으로 두 번째 공식은 첫 번째 공식에 연쇄 법칙을 적용하여 얻어집니다.
아크사인은 사인의 역함수이므로 역사인이라고도 합니다.
아크사인 파생물의 예
아크사인 도함수의 공식이 무엇인지 확인한 후 이러한 유형의 삼각 도함수에 대한 몇 가지 예를 설명하겠습니다. 이렇게 하면 함수의 아크사인이 어떻게 파생되는지 이해하는 것이 더 쉬울 것입니다.
예 1: 2x 아크사인의 파생
![]()
아크사인 함수의 미분을 찾으려면 해당 공식을 사용해야 합니다.
![]()
따라서 2x의 도함수는 2이므로 2x의 아크사인 도함수는 2를 1의 루트에서 2x 제곱을 뺀 값으로 나눈 값입니다.
![]()
예 2: x 제곱의 아크사인 파생
![]()
이를 도출하기 위해 아크사인 파생 공식을 사용합니다.
![]()
함수 x 2 는 2차이므로 그 도함수는 2x입니다. 따라서 x의 아크사인을 2제곱한 도함수는 다음과 같습니다.
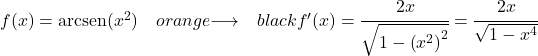
예 3: e x 아크사인의 파생
![]()
이 예의 함수는 복합 함수이므로 도함수를 풀기 위해 체인 규칙을 적용해야 합니다.
![]()
e x 의 도함수는 그 자체이므로 전체 함수의 도함수는 다음과 같습니다.
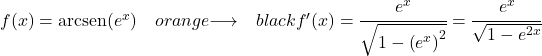
아크사인 파생 문제 해결
다음 아크사인 함수를 도출합니다.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
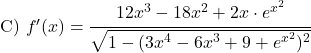
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a82c0fd18a8672100ed3b79525a1028_l3.png)
아크사인 파생 공식 증명
다음으로 아크사인 도함수 공식의 수학적 증명을 진행합니다.
![]()
먼저 아크사인을 사인으로 변환합니다.
![]()
이제 우리는 방정식의 양쪽을 구별합니다:
![]()
우리는 당신을 정리합니다:
![]()
다음으로 기본적인 삼각법적 항등식을 적용합니다.
![]()
![]()
그리고 위에서 x가 y의 사인과 동일하다고 추론한 것처럼 동일성은 그대로 유지됩니다.
![]()
보시다시피, 이 절차를 적용하여 아크사인 함수의 미분 공식을 얻었으므로 공식이 충족되는 것으로 나타났습니다.