이 기사에서는 함수의 측면 극한이 무엇인지 설명합니다(예제 포함). 또한 그래프와 수치를 통해 함수의 왼쪽 및 오른쪽 측면 한계를 계산하는 방법을 알려드립니다. 또한, 측면 한계를 단계별로 풀어가는 운동으로 트레이닝을 할 수 있습니다.
측면 한계는 무엇입니까?
한 지점에서 함수의 측면 한계는 해당 지점 주변의 함수 동작을 연구합니다. 왼쪽 측면 극한과 오른쪽 측면 극한이 있는데, 이는 고려되는 지점의 왼쪽과 오른쪽에 대한 함수 값을 각각 분석합니다.
왼쪽 및 오른쪽 측면 제한
측면 경계의 정의에서 살펴본 것처럼 왼쪽 측면 경계와 오른쪽 측면 경계의 두 가지 유형이 있습니다.
함수의 왼쪽 극한은 극한을 분석하는 지점에서 마이너스 기호로 표시되고, 오른쪽 극한은 플러스 기호로 표시됩니다.
왼쪽의 측면 제한
![]()
오른쪽의 측면 제한
![]()
측면 한계의 의미를 더 잘 이해하려면 다음 예를 살펴보십시오.
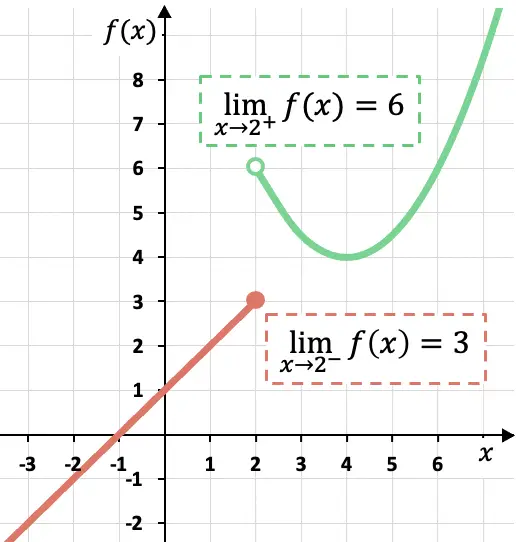
이 조각별 함수의 그래픽 표현에서 볼 수 있듯이 측면 한계는 계산되는 측면에 따라 달라집니다.
이 경우 함수는 x가 왼쪽에서 x=2에 가까워질수록 3에 가까운 값을 취하므로 x가 왼쪽에서 2에 가까워질수록 함수는 3에 가까워집니다.
반면 x=2에서 선으로 함수의 측면 극한은 6의 가치가 있습니다. 왜냐하면 선으로 x=2 지점에 접근하면 함수는 f(x)=에 점점 더 가까운 값을 취하기 때문입니다. 6.
반면, 측면 한계는 일반 한계와 동일한 속성을 갖는다는 것을 알아야 합니다. 다음 링크에서 경계 속성이 무엇인지 확인할 수 있습니다.
➤ 참고: 경계 속성
동등한 측면 한계
방금 함수의 측면 한계가 다른 예를 보았습니다. 하지만… 측면 한계가 동일하면 어떻게 될까요?
한 점에서 함수의 측면 극한이 모두 존재하고 같으면 함수의 극한은 해당 점에 존재하며 극한의 결과는 측면 극한의 값입니다.
즉, 한 점에서 함수의 극한이 존재하려면 다음 조건을 만족해야 합니다.
![]()
따라서 한 점에서 함수의 측면 극한이 다른 경우 해당 점에서 함수의 극한은 존재하지 않습니다.
또한, 한 점에서 함수의 극한이 존재한다는 것은 그것이 한 점에서 연속함수 이기 위한 필수조건이다.
측면 한계의 개념을 완전히 이해하기 위해 예를 풀어보겠습니다.

그래픽으로 표현된 함수의 x=-2 지점에서 측면 한계는 일치합니다. 왜냐하면 함수의 값은 왼쪽에서 x=-2에 접근하든 오른쪽에서 접근하든 관계없이 3을 향하는 경향이 있기 때문입니다. 따라서 x=-2에서 함수의 극한은 3과 같습니다.
![]()
반면, x=4 지점에서는 측면 한계가 다릅니다. 왜냐하면 왼쪽에서 함수는 f(x)=3에 접근하지만 오른쪽에서는 함수가 f(x)=2에 접근하기 때문입니다. 따라서 이 시점에서 기능의 한계는 존재하지 않습니다.
![]()
측면 한계 계산
측면 한계의 정의가 주어지면 다음 예를 풀어 수치적으로 계산하는 방법을 살펴보겠습니다.
![]()
평소대로 극한을 계산하면 실수를 0으로 나눈 불확정성을 얻습니다.
![]()
그러나 측면 한계를 계산할 때 불확정성은 발생하지 않습니다.
![]()
x=2에서 왼쪽부터 함수의 측면 극한을 계산하려면 x=2보다 작지만 x=1.999와 매우 가까운 숫자를 사용해야 합니다.
![]()
이 경우 분모는 매우 작은 값을 갖는 음수이지만 0도 아니며 일반적으로 분모 앞에 0과 빼기 기호가 표시됩니다.
![]()
따라서 측면 극한의 결과는 음의 무한대입니다. 0으로 나눈 모든 숫자는 무한대를 제공하고 양수를 음수로 나누면 음수를 제공하기 때문입니다.
![]()
왼쪽부터 x=2에 가까운 값을 갖는 함수의 이미지를 계산하여 함수가 음의 무한대에 가까워지는 것을 확인할 수 있습니다.
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1,9)=\cfrac{3}{1,9-2}=-30\\[2ex]f(1,99)=\cfrac{3}{1,99-2}=-300\\[2ex]f(1,999)=\cfrac{3}{1,999-2}=-3000\\[2ex]f(1,9999)=\cfrac{3}{1,9999-2}=-30000\\[2ex]f(1,99999)=\cfrac{3}{1,99999-2}=-300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^-)=-\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-97d799f09c2e0890cf3a856bf9c711a2_l3.png)
마찬가지로, 오른쪽의 x=2 지점에서 함수의 극한을 찾기 위해 동일한 추론을 적용할 수 있습니다. 즉, 2001과 같이 2보다 크지만 매우 가까운 값을 사용합니다.
![]()
같은 방법으로 오른쪽에서 x=2에 가까울수록 값이 가까운 함수의 이미지를 계산하여 함수가 무한대를 향하는 경향이 있음을 확인할 수 있습니다.
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(2,1)=\cfrac{3}{2,1-2}=30\\[2ex]f(2,01)=\cfrac{3}{2,01-2}=300\\[2ex]f(2,001)=\cfrac{3}{2,001-2}=3000\\[2ex]f(2,0001)=\cfrac{3}{2,0001-2}=30000\\[2ex]f(2,00001)=\cfrac{3}{2,00001-2}=300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^+)=+\infty\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6d448cdad3ac6ba82e749b30d2bcc11_l3.png)
다음 그래프에서 분석된 함수를 볼 수 있습니다. 보시다시피, 왼쪽 x=2 지점에서 함수의 측면 극한은 음의 무한대이고, 오른쪽 x=2 지점에서 함수의 측면 극한은 플러스 무한대입니다.

측면 경계 문제가 해결되었습니다.
연습 1
정의가 변경되는 지점(x=-2 및 x=4)에서 다음 조각별로 정의된 함수의 측면 극한을 찾습니다.

측면 한계는 x=-2 지점에서 일치하지 않습니다. 왼쪽에서 함수는 f(x)=5를 향하는 경향이 있고, 반면 오른쪽에서는 함수가 상수이고 값이 3입니다.
![]()
![]()
x가 4에 접근하면 측면 한계도 다릅니다. 조각별 함수는 왼쪽에서 3에 접근하지만 오른쪽에서 -2에 접근합니다.
![]()
![]()
연습 2
x가 다음 조각 함수의 3에 접근할 때 극한이 존재하는지 확인하고, 그렇다면 그 값은 무엇입니까?
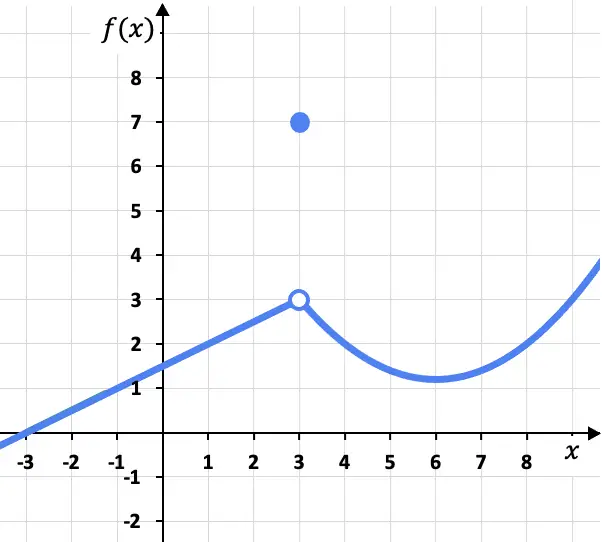
이 문제에서는 왼쪽과 오른쪽에서 점 x=3의 측면 한계가 동일합니다. 왜냐하면 함수는 왼쪽에서 접근하든 오른쪽에서 접근하든 동일한 값(f(x)=3)을 향하는 경향이 있기 때문입니다. . 그의 오른쪽:
![]()
![]()
따라서 극한의 수학적 정의에 따르면 x가 3으로 경향일 때 함수의 극한은 3과 같습니다. 왜냐하면 이 동일한 지점의 두 측면 극한이 이 값에서 일치하기 때문입니다.
![]()
x=3에서의 함수의 극한은 3이지만, 이 시점에서의 함수는 3이 아니라 f(3)=7이라는 점을 고려해야 합니다. 나중에 살펴보겠지만 이는 함수가 x=3에서 연속이 아니라 피할 수 있는 불연속성을 갖는다는 것을 의미합니다.
연습 3
x=4 지점에서 다음 유리 함수의 측면 한계를 계산합니다.
![]()
x가 왼쪽에서 4에 가까워질 때의 한계를 계산하려면 4보다 작지만 매우 가까운 값(예: 3,999)을 사용합니다.
![]()
따라서 x가 왼쪽에서 4에 접근할 때 측면 극한은 플러스 무한대입니다.
그리고 x가 오른쪽에서 4로 향할 때 극한을 해결하기 위해 4보다 크지만 이에 매우 가까운 값(예: 4,001)에서 함수를 평가합니다.
![]()
따라서 x가 오른쪽에서 4에 접근할 때 측면 극한은 음의 무한대입니다.
연습 4
x=2 지점에 정의된 다음 조각별 함수의 극한이 존재하는 경우 이를 구합니다.
![\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”75″ width=”235″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-40d5632016e70b9d9ab8e46e76e0102b_l3.png)