이 기사에서는 제한된(상위 및 하위) 함수가 무엇인지 설명합니다. 또한 함수가 한 지점에 묶여 있다는 것이 무엇을 의미하는지 보여주고 마지막으로 이러한 유형의 함수의 속성을 찾을 수 있습니다.
제한된 함수란 무엇입니까?
유계함수(bounded function) 는 그래프가 경계 내에 있는 함수입니다. 즉, K보다 큰 함수의 값(f(x)≤K)이 존재하지 않는 숫자 K가 존재하면 함수는 위에 제한되고, K보다 큰 숫자 K가 존재하면 함수는 아래에 제한됩니다. 함수의 모든 값(f(x)≥K)보다 작습니다. 따라서 유계함수는 위와 아래에 유계가 있는 함수입니다.
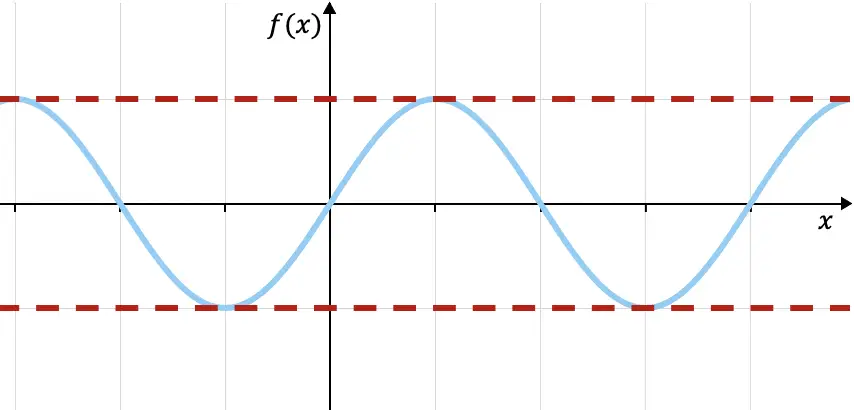
예를 들어, 위에 그래프로 표시된 삼각 사인 함수는 위쪽은 f(x)=1로 제한되고 아래쪽은 f(x)=-1(빨간색 점선)로 제한됩니다. 기능은 이 두 가지 제한 내에 있습니다. 다음 링크에서 이 함수의 추가 속성을 볼 수 있습니다.
➤ 참조: 사인 함수의 특성
위에 제한된 함수
그러나 모든 기능이 위와 아래로 제한되는 것은 아니며, 함수는 위나 아래로만 제한될 수 있습니다.
위의 제한된 함수는 특정 값을 초과하지 않는 함수, 즉 다음 조건을 충족하는 함수입니다.
![]()
여기서 K 값은 함수의 상한입니다.
예를 들어, 다음 포물선은 위쪽이 K=7로 제한되어 있지만 함수의 가지가 무한대로 확장되므로 함수의 아래쪽은 제한되지 않습니다.

논리적으로 함수가 K=7로 제한되면 K=8 이상의 값으로도 제한됩니다.
가장 작은 상한을 상한이라고 하며 sup(f) 로 표시합니다. 더욱이 함수가 해당 영역에서 상기 상한에 도달하면 이 지점이 함수의 절대 최대값 이라고 말할 것입니다.
➤ 참고: 함수의 최대값과 최소값은 무엇인가요?
우리의 경우 함수는 기하학적으로 K=7로 제한되어 있으므로 이는 함수의 상한 극값이자 절대 최대값입니다.
아래에 구분된 함수
아래에 구분된 함수는 특정 숫자보다 작은 값을 가지지 않는 함수, 즉 다음 수식을 만족하는 함수입니다.
![]()
여기서 K 값은 함수의 하한입니다.
아래에는 K=3으로 구분되는 지수 함수의 그래픽 표현이 있습니다.

분명히 함수는 K=3보다 작은 값으로 제한됩니다.
이전과 마찬가지로 가장 큰 하한을 하한이라고 하며 inf(f) 로 표시합니다. 더욱이 함수가 해당 영역에서 더 낮은 극단에 도달하면 이 지점이 함수의 절대 최소 점이라고 말할 것입니다.
이 경우 K=3은 함수의 절대 최소값이 아닙니다. 왜냐하면 함수가 무한대에서 이 값에 도달하고 따라서 해당 영역 외부에 있기 때문입니다. 즉, f(x)=3은 함수 의 수평 점근선 입니다.
그래픽 표현 없이 함수가 위쪽과 아래쪽에 제한되어 있는지 알 수 있는 정리가 있습니다. Weierstrass의 정리가 무엇인지 보려면 여기를 클릭하십시오.
➤ 참조: Weierstrass 정리
한 지점에 제한된 함수
우리는 방금 함수의 경계 개념을 전반적으로 연구했지만, 함수가 더 작은 이웃, 즉 함수의 일부에 경계가 있는지 여부를 분석하는 것도 가능합니다.
응
![]()
는 함수 영역의 한 점이고
![]()
어떤 값이든 함수는 해당 지점의 위/아래에 제한되어 있다고 말할 수 있습니다.
![]()
환경이 있다면
![]()
여기서 함수는 위/아래로 제한됩니다.
따라서 함수는 점에 국한됩니다.
![]()
동네의 위쪽과 아래쪽으로 구분되어 있는 경우
![]()
분명히, 함수가 일반적으로 유계라면 함수의 각 지점에서도 유계가 있을 것입니다. 그러나 그 반대는 거짓입니다. 즉, 함수는 각 점에서 제한될 수 있지만 전체 영역에 걸쳐 제한될 수는 없습니다.
예를 들어, 다음 아핀 함수는 각 점에서 부분적으로 유계이지만 유계 함수는 아닙니다.

제한된 함수의 속성
제한된 함수에는 다음과 같은 속성이 있습니다.
- 응

그리고

두 개의 경계 함수, 두 함수의 덧셈(또는 뺄셈)입니다.
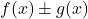
또한 제한된 함수입니다.
- 응

그리고

두 개의 경계 함수는 두 함수의 곱입니다.
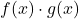
또한 제한된 함수이기도 합니다.
- 함수에 수직 점근선이 있으면 완전히 유계일 수 없습니다. 반면에 함수는 위 또는 아래로 제한될 수 있습니다.
- 구간의 모든 연속 및 유계 함수는 적분 가능합니다.