정규 또는 역행렬

이 페이지에서는 정규 또는 역행렬에 대한 설명과 행렬의 역전이 수행될 수 있는 시기와 수행되지 않는 시기를 아는 방법을 찾을 수 있습니다. 또한 개념을 완전히 이해하기 위해 정규 행렬의 몇 가지 예도 볼 수 있으며 마지막으로 이러한 유형의 행렬의 모든 속성을 보여줍니다.

정규 행렬이란 무엇입니까?

정규행렬의 정의는 다음과 같습니다.

정규 행렬은 역행렬이 가능한 정사각 행렬입니다. 즉, 해당 행렬의 역행렬을 계산할 수 있습니다. 따라서 행렬식은 0이 아닙니다.

정규 행렬은 가역 행렬, 비특이 행렬, 비퇴화 행렬 이라고도 합니다.

정규행렬의 반대행렬은 특이행렬 또는 축퇴행렬이다.

따라서 행렬이 정규행렬인지 특이행렬인지, 즉 행렬이 가역행렬인지 아닌지를 알기 위해서는 행렬의 행렬식을 풀면 충분합니다.

행렬의 행렬식이 0이 아닌 경우 행렬은 정규 또는 가역 행렬입니다.

행렬의 행렬식이 0이면 행렬은 특이 행렬이거나 역행렬이 아닙니다.

결론적으로 행렬의 행렬식을 계산하는 것은 행렬에 역행렬이 있는지 여부를 알 수 있는 가장 간단한 방법이므로 모든 행렬의 가역성을 결정하는 데 권장되는 방법입니다.

행렬을 반전시키는 방법을 알고 싶다면 행렬을 반전시키는 방법을 단계별로 설명하는 역행렬 공식을 확인하세요. 또한 연습할 수 있는 여러 예제와 해결된 연습문제도 찾을 수 있습니다.

정규 또는 역행렬의 예

정규 또는 역행렬의 의미를 확인한 후에는 다양한 차원의 정규 행렬의 몇 가지 예를 살펴보겠습니다.

일반 또는 반전 가능한 2×2 행렬의 예

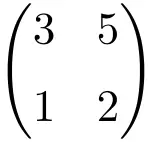
행렬식을 계산하여 정규 행렬임을 확인할 수 있습니다.

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

2차 행렬의 행렬식은 0과 다르기 때문에 정규행렬이다.

일반 또는 반전 가능한 3×3 행렬의 예

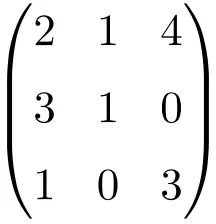
역행렬인지 확인하려면 행렬의 행렬식을 만들어야 합니다.

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

3차 행렬의 행렬식은 0이 아닌 결과를 나타내므로 정규 행렬입니다.

일반 또는 반전 가능한 4×4 행렬의 예

행렬의 행렬식을 취하면 이것이 정규 행렬임을 알 수 있습니다.

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

4차 행렬의 행렬식은 0이 아니므로 역행렬입니다.

경고: 행렬식 계산에 대해 의문이 있는 경우 행렬식 계산 방법 페이지를 참조할 수 있습니다.

일반 또는 가역 행렬의 속성

정규 또는 가역행렬은 선형대수학에서 매우 중요하며 이는 다음과 같은 특징 때문입니다.

A가 역행렬인 경우 전치 행렬 또는 전치 행렬도 마찬가지입니다. 또한 전치의 역행렬은 역행렬의 전치와 같습니다.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

정규 행렬의 범위는 항상 가능한 최대값입니다. 즉, 범위는 행렬의 차원과 동일합니다.

두 개의 가역 행렬 사이의 행렬 곱은 또 다른 정규 행렬을 생성합니다. 이 조건은 행렬식의 속성을 사용하여 쉽게 설명할 수 있습니다.

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

모든 직교행렬은 동시에 정규행렬이다.

A를 선형 방정식 시스템을 나타내는 행렬로 설정합니다.
$(Ax=b)$

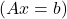
, A가 정규 행렬인 경우 시스템은 고유한 솔루션을 가지므로 SCD(호환 결정 시스템)입니다.

또한 시스템이 동종 시스템인 경우
$(Ax=0)$

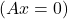
A가 반전될 수 있으면 시스템의 해는 간단합니다.

$x=0.$

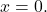
일반 행렬의 열과 행은 서로 선형 독립입니다.

정규 또는 역행렬의 모든 고유값(또는 고유값)은 0이 아닙니다.

일반 금 반전 매트릭스