여기에서는 차이(또는 빼기)의 제곱에 대한 주목할만한 항등 공식이 무엇인지 설명합니다. 즉, 표현식 (ab) 2 가 어떻게 해결되는지 보여줍니다. 또한 차이의 제곱에 맞춰 풀 수 있는 연습문제와 예시를 볼 수 있습니다. 그리고 마지막으로 이 놀라운 제품 유형의 공식 시연과 기하학적 해석을 보여줍니다.
차이(또는 빼기)의 제곱은 무엇입니까?
차이의 제곱 또는 빼기의 제곱은 주목할만한 항등식 (또는 주목할만한 곱) 중 하나입니다. 즉, 두 항이 있는 이항식의 구적법 계산을 용이하게 하는 수학적 규칙으로 구성됩니다. 다른 하나는 부정적입니다.
따라서 차이의 제곱에 대한 대수적 표현은 (ab) 2 입니다.
차이의 제곱(또는 빼기) 공식
이러한 유형의 놀라운 정체성에 대한 정의를 확인한 후에는 공식을 사용하여 차이의 제곱을 푸는 방법을 살펴보겠습니다.

따라서 차이의 제곱은 첫 번째 항의 제곱에서 첫 번째 항과 두 번째 항의 곱의 두 배를 빼고 두 번째 항의 제곱을 더한 것과 같습니다.
따라서 차이 또는 제곱 뺄셈을 계산하려면 각 항을 2로 올릴 뿐만 아니라 함께 곱하고 2를 곱해야 합니다.
제곱을 뺄 때 매우 흔히 저지르는 실수는 두 항 사이에 곱을 넣지 않고 감소의 제곱과 뺄셈의 뺄셈만 푸는 것이기 때문에 이를 기억하는 것이 중요합니다.

a와 b 사이의 제품을 잊지 마세요!
차이(또는 빼기) 제곱의 예
이제 차이의 제곱에 대한 공식을 알았으니 이를 이용해 계산을 할 수 있습니다. 이것이 어떻게 이루어지는지 볼 수 있도록 차이의 제곱(또는 빼기)에 대한 몇 가지 해결된 예를 준비했습니다.
실시예 1
- 다음 차이의 제곱을 풀어보세요.
![]()
제곱 빼기이므로 다음 공식을 적용해야 합니다.
![]()
따라서 우리는 미지의 값이 무엇인지 식별해야 합니다.
![]()
그리고
![]()
공식의. 이 경우,
![]()
변수입니다
![]()
그리고
![]()
숫자 3에 해당합니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
음수 기호는
![]()
하지만 공식을 올바르게 적용하려면 항상 부호 없이 숫자를 사용해야 합니다.
그러므로 우리는 이미 다음의 가치를 알고 있습니다.
![]()
그리고
![]()
따라서 이 값을 공식에 대입하면 됩니다.

실시예 2
- 제곱 빼기의 다음 이항식을 계산합니다.
![]()
차이의 제곱에 대한 공식은 다음과 같습니다.
![]()
그러므로 우리는 먼저 다음의 가치를 식별해야 합니다.
![]()
그리고
![]()
공식의. 이 문제에서는
![]()
단항식을 나타냅니다
![]()
그리고
![]()
이항식의 독립항, 즉 2와 동일합니다.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-868a41eb665f5bc94959448547c060d5_l3.png)
마지막으로 매개변수의 값을 알고 나면
![]()
그리고
![]()
, 우리는 단순히 제곱 빼기에 대한 이항 공식을 적용합니다:
![Rendered by QuickLaTeX.com \begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5e88231a654b23a306e53e17d175d25_l3.png)
차이의 제곱에 대한 공식 증명
그런 다음 뺄셈의 제곱 공식이 어디서 나오는지 추론해 보겠습니다. 비록 증명을 외울 필요는 없지만 그 이면의 수학을 이해하는 것은 여전히 좋습니다.
모든 뺄셈의 이항식 표현에서 시작하면:
![]()
분명히 이전 전력은 요인의 곱과 같습니다.
![]()
자체적으로 곱한 것 :
![]()
이제 분배 법칙을 적용하여 두 괄호를 곱합니다.
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
그리고 공식 증명을 완료하려면 유사한 용어를 그룹화하면 됩니다.
![]()
뺄셈의 제곱에 대한 공식을 수학적으로 증명하려면:
![]()
호기심으로 제곱 빼기의 이항식을 전개한 것을 완전제곱삼항식이라고도 합니다.
차이의 제곱에 대한 기하학적 해석
차이의 제곱 개념에 대한 이해를 마치기 위해 이 놀라운 동등성을 기하학적으로 해석하는 방법을 살펴보겠습니다.
변의 길이가 다른 정사각형을 보세요
![]()
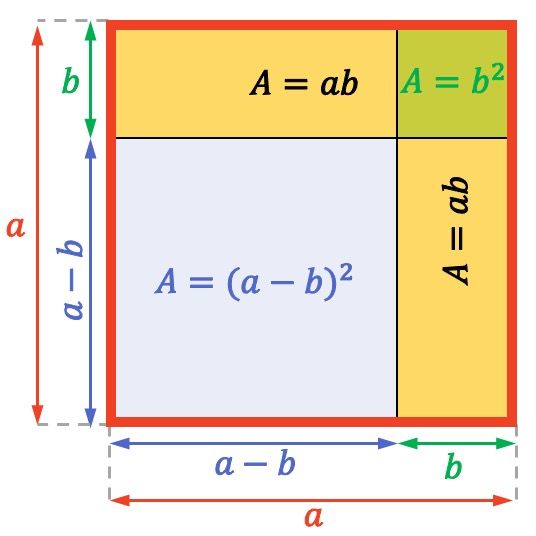
정사각형이나 직사각형의 면적(또는 표면적)은 인접한 변의 두 개를 곱하여 계산됩니다. 따라서 위의 전체 정수 정사각형의 면적은 다음과 같습니다.
![]()
마찬가지로 각 노란색 직사각형의 면적은 다음과 같습니다.
![]()
그리고 마지막으로 오른쪽 상단에 표시된 작은 사각형의 면적은
![]()
즉 한 변의 제곱은
![]()
그 표면은
![]()
1제곱제곱의 면적으로 분해될 수 있다
![]()
직사각형 치수의 2 배를 뺀 값
![]()
그리고
![]()
, 더하기 측면 사각형의 면적
![]()
간단히 말해서, 차이의 제곱에 대한 공식은 기하학적으로 검증될 수도 있습니다.
![]()
차이의 제곱(또는 빼기) 문제 해결
여러분이 연습할 수 있도록 차이의 제곱의 주목할만한 결과에 대해 단계별로 해결되는 몇 가지 연습 문제를 알려드립니다. 아래 댓글에 질문이 있으면 적어주세요.
연습 1
다음 뺄셈을 제곱하여 풀어보세요:
![]()
![]()
![]()
![]()
![]()
문제의 놀라운 정체성을 모두 찾으려면 차이의 제곱에 대한 공식을 적용하는 것으로 충분합니다.
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-138b359ce2e8f8b1012c6ecf1b7fb9b0_l3.png)
연습 2
공식을 적용하여 두 수량의 차이에 대한 다음 제곱을 결정합니다.
![]()
![]()
![]()
문제의 주목할만한 모든 곱을 결정하려면 제곱 빼기 공식을 사용해야 합니다.
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c73b9ba584f955a0cae5564a2226d465_l3.png)
섹션 B)를 풀려면 근을 제곱하면 단순화된다는 점을 기억해야 합니다.
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38cd9e9855f7f79f607247ccc731e297_l3.png)
마지막 제곱 뺄셈의 단항식은 분수 계수를 가지므로 이를 해결하려면 분수의 속성을 사용해야 합니다.
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46106420913cc7a370e2f5215af0f2a2_l3.png)