이 페이지에서는 매개변수를 사용하여 방정식 시스템을 논의하고 해결하는 방법을 살펴보겠습니다. 또한 연습할 수 있는 선형 방정식 시스템의 예제와 해결된 연습을 찾을 수 있습니다.
반면, 선형 방정식 시스템을 분석하려면 Cramer의 법칙이 무엇인지 , Rouché-Frobenius 정리가 무엇인지 아는 것이 중요합니다. 왜냐하면 우리는 이를 지속적으로 사용할 것이기 때문입니다.
매개변수가 있는 선형 방정식 시스템의 예
- 매개변수 m 을 기준으로 다음 방정식 시스템을 토론하고 풀어보세요.
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ab2286d15c20029b98a5ea4622033d4_l3.png)
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
이제 Sarrus의 규칙을 사용하여 A의 행렬식을 풀어 행렬의 순위를 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e823f83f25f798bd854612a7352680d4_l3.png)
따라서 A 행렬식의 결과는 m 값에 따라 달라집니다. 그러므로 우리는 행렬식이 사라지는 m 의 값을 볼 것입니다. 이를 위해 결과를 0으로 설정합니다 .
![]()
그리고 우리는 다음 공식을 사용하여 이차 방정식을 푼다.
![]()
![Rendered by QuickLaTeX.com \displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e863082ac1f9b43df4de9fe93f5eb305_l3.png)
따라서 m이 2 또는 3과 같을 때 A의 행렬식은 0이 됩니다. 그리고 m이 2와 다르고 3과 다를 때 A의 행렬식은 0과 달라집니다.
따라서 우리는 각 사례를 개별적으로 분석해야 합니다.
m≠3 및 m≠2:
방금 본 것처럼 매개변수 m이 2와 3과 다를 때 행렬 A의 행렬식은 0과 다릅니다. 따라서 A의 순위는 3입니다 .
![]()
더욱이, 행렬 A’의 순위도 3입니다 . 그 내부에는 행렬식이 0과 다른 3×3 부분행렬이 있기 때문입니다. 그리고 ‘4×4 행렬식을 만들 수 없기 때문에 순위 4가 될 수 없습니다.
![]()
그런 다음 행렬 A의 순위는 행렬 A’의 순위 및 시스템의 미지수 수(3)와 동일하므로 Rouché-Frobenius 정리 에 의해 SCD( 결정된 시스템 호환 )임을 알 수 있습니다. :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
시스템이 호환 가능 시스템(DCS)이라는 것을 알게 되면 이를 해결하기 위해 Cramer의 규칙을 적용합니다. 이를 수행하려면 행렬 A, 행렬식 및 행렬 A’가 다음과 같다는 점을 기억하십시오.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac47361358555f733a42cffecabdbe9_l3.png)
Cramer의 법칙으로 x를 계산하기 위해 행렬 A의 행렬식의 첫 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b17f49436fdadbb014011b5c461a4a56_l3.png)
Cramer의 법칙으로 y를 계산하기 위해 A의 행렬식의 두 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a2bf75bdabfb2c83870f1869ce19e3d_l3.png)
Cramer의 법칙으로 z를 계산하기 위해 A의 행렬식의 세 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eebb3c4d280afc8a9aed8877ddcd4ac5_l3.png)
따라서 m≠3 및 m≠2의 경우 방정식 시스템의 해는 다음과 같습니다.
![]()
보시다시피, 이 경우 연립방정식의 해는 m의 함수입니다.
m이 2와 3과 다를 때의 해를 구했다면, m이 2일 때의 해를 구해 보겠습니다.
m=2:
이제 매개변수 m 이 2일 때 시스템을 분석하겠습니다. 이 경우 행렬 A와 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f42ec4801f3e84cd44b4e0b2ae6351cf_l3.png)
이전에 보았듯이 m=2일 때 A의 행렬식은 0입니다. 따라서 행렬 A는 랭크 3이 아닙니다. 그러나 그 내부에는 0과 다른 2×2개의 행렬식이 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
따라서 이 경우 A의 순위는 2입니다 .
![]()
행렬 A의 순위를 알고 나면 A’의 순위를 계산합니다. 처음 3개 열의 행렬식은 0을 제공하므로 행렬 A’에서 다른 가능한 3×3 행렬식을 시도해 봅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c68c742cae37c52ad2566b7feec5301_l3.png)
3×3 차원의 가능한 모든 행렬식은 0입니다. 그러나 분명히 행렬 A’는 행렬 A와 동일한 2×2 비-0 행렬식을 갖습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
따라서 행렬 A’도 랭크 2입니다 .
![]()
따라서 행렬 A의 순위는 행렬 A’의 순위와 동일하지만 이 둘은 시스템(3)의 미지수 수보다 작기 때문에 Rouché-Frobenius 정리 에 의해 이것이 불확정적으로 호환 가능한 시스템 이라는 것을 알 수 있습니다. (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
ICS이기 때문에 이를 해결하려면 시스템 전환이 필요합니다. 이렇게 하려면 먼저 시스템에서 방정식을 제거해야 합니다. 이 경우 마지막 방정식을 삭제합니다.
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10c7facda35cb8894e6bbb236e4953f1_l3.png)
이제 변수 z를 λ로 변환해 보겠습니다.
![Rendered by QuickLaTeX.com \begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0155083595420da31a486927e953805c_l3.png)
그리고 우리는 독립된 항을 λ로 갖는 항을 넣습니다.
![Rendered by QuickLaTeX.com \begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8486baee4be39f417988ee12b5e67c7_l3.png)
따라서 시스템의 행렬 A와 행렬 A’는 다음과 같이 유지됩니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8591e8c21bce2f49998311bbb08f7dee_l3.png)
마지막으로 시스템을 변형한 후에 는 Cramer의 법칙을 적용합니다 . 이를 위해 먼저 A의 행렬식을 해결합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3](https://mathority.org/wp-content/ql-cache/quicklatex.com-c34669d7234c9736c350f793df337bd3_l3.png)
Cramer의 법칙으로 x를 계산하기 위해 A의 행렬식의 첫 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-987ebe052154332042afeb27535996f1_l3.png)
Cramer의 법칙으로 y를 계산하기 위해 A의 행렬식의 두 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a3c7b2cd7319f7f9db6df7df79abb50_l3.png)
따라서 m=2일 때 연립방정식의 해는 SCI이므로 무한한 해를 가지므로 λ의 함수입니다.
![]()
우리는 매개변수 m이 2와 3과 다르고 2와 같을 때 시스템의 해를 이미 분석했습니다. 따라서 우리는 마지막 경우만 필요합니다: m이 3의 값을 가질 때:
m=3:
이제 매개변수 m이 3일 때 어떤 일이 발생하는지 분석하겠습니다. 이 경우 행렬 A와 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49bbc0d7d36606aa59be050c2682de5_l3.png)
이전에 보았듯이 m=3일 때 A의 행렬식은 0입니다. 따라서 행렬 A는 랭크 3이 아닙니다. 그러나 그 내부에는 0과 다른 2×2개의 행렬식이 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d88ce42feb4bba9aa74aae98e1062c4a_l3.png)
따라서 이 경우 A의 순위는 2입니다 .
![]()
행렬 A의 순위를 알고 나면 A’의 순위를 계산합니다. 처음 3개 열의 행렬식은 0을 제공하므로 행렬 A’ 내부에 있는 또 다른 3×3 행렬식을 시도합니다(예: 마지막 3개 열의 행렬식).
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e6f1a5c155ca004c73e51bdcbe5ece9_l3.png)
반면, 행렬 A’에는 결과가 0과 다른 행렬식이 포함되어 있으므로 행렬 A’는 순위 3입니다 .
![]()
따라서 m = 3일 때 행렬 A의 순위는 행렬 A’의 순위보다 낮습니다. 따라서 Rouché-Frobenius 정리에서 우리는 시스템이 호환되지 않는 시스템 (IS)이라고 추론합니다 .
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3454f804b63f3cca9bcf08bc93815f90_l3.png)
따라서 연립방정식은 m = 3일 때 해를 갖지 않습니다.
예제 요약:
우리가 본 것처럼, 연립방정식의 해는 매개변수 m 의 값에 따라 달라집니다. 가능한 모든 사례를 요약하면 다음과 같습니다.
- m≠3 및 m≠2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf366a55bd307517f94fd8aa00cdf598_l3.png)
- m=2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94002d4f4d866569ed7d6993dd977b81_l3.png)
- m=3:
![]()
시스템에는 해결책이 없습니다.
여기에서는 Rouche의 정리와 Cramer의 법칙을 사용하여 전체 과정을 수행했지만 매개변수가 있는 방정식 시스템은 Gauss의 방법(연습 포함) 으로 논의하고 풀 수도 있습니다. 링크된 페이지에서 이 방법에 대해 자세히 알아볼 수 있으며, 여기에서 절차에 대한 자세한 설명은 물론 예제와 해결된 연습 문제를 단계별로 찾을 수 있습니다.
매개변수가 있는 선형 방정식 시스템의 토론 문제 해결
연습 1
다음과 같은 매개변수 의존 선형 방정식 시스템을 토론하고 풀어보세요.
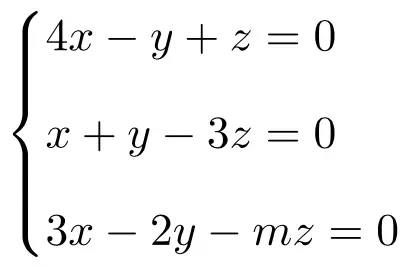
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b641845325965882d4aac899246cffb3_l3.png)
이제 행렬 A의 순위를 찾아야 합니다. 이를 위해 전체 행렬의 행렬식이 0과 다른지 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d36c7cffe0248a2f45cd5871abc6ed5_l3.png)
A의 행렬식의 결과는 m의 값에 따라 달라집니다. 그러므로 우리는 행렬식이 사라지는 m의 값을 볼 것입니다. 이를 위해 결과 결과를 0과 동일하게 하고 방정식을 풉니다.
![]()
![]()
![]()
따라서 m이 -4일 때 A의 행렬식은 0이 됩니다. 그리고 m이 -4와 다르면 A의 행렬식은 0과 다를 것입니다. 따라서 각 경우를 개별적으로 분석해야 합니다.
m≠-4:
방금 본 것처럼 매개변수 m이 -4와 다를 때 행렬 A의 행렬식은 0과 다릅니다. 따라서 A의 순위는 3입니다.
![]()
게다가 행렬 A’의 순위도 3입니다. 그 안에 행렬식이 0과 다른 3×3 부분행렬이 있기 때문입니다. 그리고 ‘4×4 행렬식을 만들 수 없으므로 순위 4가 될 수 없습니다.
![]()
따라서 Rouché-Frobenius 정리를 적용하면 A의 범위가 A’의 범위 및 미지수의 개수와 동일하므로 이것이 호환 가능한 결정계 (SCD)임을 알 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
시스템이 SCD라는 것을 알게 되면 이를 해결하기 위해 Cramer의 규칙을 적용합니다. 이를 수행하려면 행렬 A, 행렬식 및 행렬 A’가 다음과 같다는 점을 기억하십시오.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9e0bd352ad7713a03824ead1239041c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20](https://mathority.org/wp-content/ql-cache/quicklatex.com-530cb4576ee1a91d6246ed6cf9dd0fc8_l3.png)
xatex]를 Cramer의 법칙으로 계산하기 위해 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b076bbda8d086abedb459570d74c80a9_l3.png)
미지수를 계산하기 위해 Cramer의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f642a8cb2fd174e5c383a4df53e11a2e_l3.png)
Cramer의 법칙으로 z를 계산하기 위해 A의 행렬식의 세 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5020a9ba4995b9715d8d1fb4720952b1_l3.png)
따라서 m≠-4인 경우의 연립방정식의 해는 다음과 같습니다.
x=0 y=0 z=0
m=-4:
이제 매개변수 m이 -4일 때 시스템을 분석하겠습니다. 이 경우 행렬 A와 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e585e6465d27ea27ccc2c1a6ec1fe9ae_l3.png)
이전에 보았듯이 m=-4일 때 A의 행렬식은 0입니다. 따라서 행렬 A는 랭크 3이 아닙니다. 그러나 그 내부에는 0과 다른 2×2 행렬식이 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
행렬이 0과 다른 2차 행렬식을 가지므로 행렬 A는 랭크 2입니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 다른 가능한 3×3 행렬식을 시도해 봅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-39fc49c7a63920c8956703a4851ecfc0_l3.png)
행렬 A’의 모든 3×3 행렬식은 0이므로 행렬 A’도 순위 3이 아닙니다. 그러나 그 내부에는 0과 다른 차수 2의 결정자가 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
따라서 행렬 A’는 순위 2가 됩니다.
![]()
행렬 A의 범위는 행렬 A’의 범위와 동일하지만 이 두 개는 시스템(3)의 미지수 수보다 작습니다. 따라서 Rouché-Frobenius 정리에 따르면 c는 불확정 호환 시스템(ICS)입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f43fdf4978386c61d18f9bb5b5883881_l3.png)
ICS 시스템이므로 이를 해결하려면 시스템 전환이 필요합니다. 먼저 하나의 방정식을 제거합니다. 이 경우 마지막 방정식이 됩니다.
![Rendered by QuickLaTeX.com \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d5499fda37d3cbf56fbf6ecbfc6bfba_l3.png)
이제 변수 z를 λ로 변환해 보겠습니다.
![Rendered by QuickLaTeX.com \begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96ea68274b072531365282e01d926718_l3.png)
그리고 우리는 독립된 항을 λ로 갖는 항을 넣습니다.
![Rendered by QuickLaTeX.com \begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6192715e62cc8e3d3fe4c51da8629c70_l3.png)
시스템의 행렬 A와 행렬 A’는 다음과 같이 유지됩니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-99a91208ff1742f81e799aa5ab7f9097_l3.png)
마지막으로 시스템을 변형한 후에는 Cramer의 법칙을 적용합니다. 이를 위해 먼저 A의 행렬식을 해결합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5](https://mathority.org/wp-content/ql-cache/quicklatex.com-34832b783ddaf4af205302240d0feafb_l3.png)
Cramer의 법칙으로 x를 계산하기 위해 A의 행렬식의 첫 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-362167d2eaa02d7243dedd5c385d08b1_l3.png)
미지수를 계산하기 위해 Cramer의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ede5a3a87ac0bb9ceea4232ec7b381fd_l3.png)
따라서 m=-4일 때 연립방정식의 해는 SCI이고 따라서 무한한 해를 가지므로 λ의 함수입니다.
![]()
연습 2
다음과 같은 매개변수 의존 선형 방정식 시스템에 대한 해를 토론하고 찾아보세요.
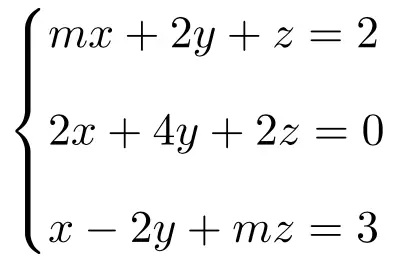
가장 먼저 해야 할 일은 시스템의 행렬 A와 확장 행렬 A’입니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
이제 행렬 A의 순위를 찾아야 합니다. 이를 위해 전체 행렬의 행렬식이 0과 다른지 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d0f8dbb7408ac6521e0144ac2f3a8a3_l3.png)
A의 행렬식의 결과는 m의 값에 따라 달라집니다. 그러므로 우리는 행렬식이 사라지는 m의 값을 볼 것입니다. 이를 위해 결과 결과를 0과 동일하게 하고 방정식을 풉니다.
![]()
![]()
![]()
![]()
![]()
따라서 m이 +1 또는 -1일 때 A의 행렬식은 0이 됩니다. 그리고 m이 +1 및 -1과 다를 때 A의 행렬식은 0과 다를 것입니다. 따라서 각 경우를 다음과 같이 분석해야 합니다.
m≠+1 및 m≠-1:
방금 본 것처럼 매개변수 m이 +1 및 -1과 다를 때 행렬 A의 행렬식은 0과 다릅니다. 따라서 A의 순위는 3입니다.
![]()
게다가 행렬 A’의 순위도 3입니다. 그 안에 행렬식이 0과 다른 3×3 부분행렬이 있기 때문입니다. 그리고 ‘4×4 행렬식을 만들 수 없으므로 순위 4가 될 수 없습니다.
![]()
따라서 Rouché-Frobenius 정리를 적용하면 A의 범위가 A’의 범위 및 미지수의 개수와 동일하므로 이것이 호환 가능한 결정계 (SCD)임을 알 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
시스템이 SCD라는 것을 알게 되면 이를 해결하기 위해 Cramer의 규칙을 적용합니다. 이를 수행하려면 행렬 A, 행렬식 및 행렬 A’가 다음과 같다는 점을 기억하십시오.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5114be5e37d2c91f02f22fba22edc42_l3.png)
Cramer의 법칙으로 x를 계산하기 위해 A의 행렬식의 첫 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b7402e02ee62bd78a6f880d3d122119_l3.png)
미지수를 계산하기 위해 Cramer의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-551c66a9530d0195a9a4ff64d42350c4_l3.png)
Cramer의 법칙으로 z를 계산하기 위해 A의 행렬식의 세 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-28375ce522b7644a745a9adea4c78ae7_l3.png)
따라서 m≠+1 및 m≠-1의 경우 방정식 시스템의 해는 다음과 같습니다.
![]()
m=+1:
이제 매개변수 m이 1일 때 시스템을 분석하겠습니다. 이 경우 행렬 A와 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6af272a99ed7c281ee8dd9199698686_l3.png)
이전에 보았듯이 m=+1일 때 A의 행렬식은 0입니다. 따라서 행렬 A는 랭크 3이 아닙니다. 그러나 그 내부에는 0과 다른 2×2개의 행렬식이 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ebedf6c9e4316844dc99ceca9472fac5_l3.png)
행렬이 0과 다른 2차 행렬식을 가지므로 행렬 A는 랭크 2입니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 이제 예를 들어 마지막 3개 열의 행렬식을 사용해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d0109b155be9f87a0cee337ddec5517_l3.png)
반면, 행렬 A’에는 결과가 0과 다른 3×3 행렬식이 포함되어 있으므로 행렬 A’는 순위 3입니다.
![]()
따라서 m=+1일 때 행렬 A의 순위는 행렬 A’의 순위보다 작습니다. 따라서 Rouché-Frobenius 정리로부터 우리는 시스템이 호환되지 않는 시스템(IS)이라고 추론합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
따라서 연립방정식은 m=+1 일 때 호환되지 않는 연립방정식이므로 해가 없습니다 .
m=-1:
이제 매개변수 m이 -1일 때 시스템을 분석하겠습니다. 이 경우 행렬 A와 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-46b0a00ef38d0e5a433b418de7eb1ec3_l3.png)
이전에 보았듯이 m=-1일 때 A의 행렬식은 0입니다. 따라서 행렬 A는 랭크 3이 아닙니다. 그러나 그 내부에는 0과 다른 2×2개의 행렬식이 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff5373c7e7901f253421efbbd52d192e_l3.png)
행렬이 0과 다른 2차 행렬식을 가지므로 행렬 A는 랭크 2입니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 이제 예를 들어 열 1, 3, 4의 행렬식을 사용해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20](https://mathority.org/wp-content/ql-cache/quicklatex.com-a95e30910bd64db920f3c2bcb5f2ff62_l3.png)
반면, 행렬 A’에는 결과가 0과 다른 3×3 행렬식이 포함되어 있으므로 행렬 A’는 순위 3입니다.
![]()
따라서 m = -1일 때 행렬 A의 순위는 행렬 A’의 순위보다 낮습니다. 따라서 Rouché-Frobenius 정리로부터 우리는 시스템이 호환되지 않는 시스템(IS)이라고 추론합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
따라서 연립방정식은 m=-1 일 때 호환되지 않는 연립방정식이므로 해가 없습니다 .