이 페이지에서는 Rouché Frobenius 정리가 무엇인지, 그리고 이를 사용하여 행렬의 순위를 계산하는 방법을 알아봅니다. 또한 Rouché-Frobenius 정리를 사용하여 단계별로 해결되는 예제와 연습 문제도 찾을 수 있습니다.
루셰-프로베니우스 정리란 무엇입니까?
Rouché-Frobenius 정리는 선형 방정식 시스템을 분류하는 방법입니다. 즉, Rouché-Frobenius 정리는 연립방정식을 풀 필요 없이 몇 개의 해가 있는지 알아내는 데 사용됩니다.
연립방정식에는 3가지 유형이 있습니다.
- SCD(시스템 호환 여부 결정): 시스템에는 고유한 솔루션이 있습니다.
- 불확정 호환 시스템(ICS): 시스템에는 무한한 해가 있습니다.
- 시스템 비호환(SI): 시스템에 해결책이 없습니다.
또한 Rouché-Frobenius 정리를 통해 나중에 Cramer의 법칙을 사용하여 시스템을 풀 수 있습니다.
Rouché-Frobenius 정리의 진술
Rouché-Frobenius 정리는 다음과 같이 말합니다.
![]()
방정식 시스템의 미지수의 계수로 구성된 행렬입니다. 그리고 배
![]()
, 또는 확장 행렬 은 방정식 시스템의 미지수 계수와 독립 항으로 구성된 행렬입니다.
Rouché-Frobenius 정리를 통해 우리는 행렬 A와 A’의 순위에 따라 어떤 유형의 방정식 시스템을 다루고 있는지 알 수 있습니다.
- 순위(A) = 순위(A’) = 알 수 없는 개수인 경우 ⟶ 결정된 호환 시스템(SCD)
- 순위(A) = 순위(A’) < 알 수 없는 개수인 경우 ⟶ 불확정 호환 시스템(SCI)
- 범위(A)인 경우
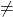
범위(A’) ⟶ 비호환 시스템(SI)
Rouché-Frobenius 정리가 무엇을 말하는지 알게 되면 Rouché-Frobenius 정리 문제를 해결하는 방법을 살펴보겠습니다. 다음은 3가지 예입니다. 각 유형의 방정식 시스템의 정리를 사용하여 해결된 연습 문제입니다.
결정된 호환 시스템(SCD)의 예
![Rendered by QuickLaTeX.com \begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6b2f93c6308c25e8df2fbb5da2af9a8_l3.png)
시스템의 행렬 A 와 확장 행렬 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-4597f5171b586bbcf0915d8512f7b89d_l3.png)
이제 행렬 A의 순위를 계산합니다. 이를 위해 전체 행렬의 행렬식이 0과 다른지 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c95b7158a2e6401cd16aeb708f128ff_l3.png)
행렬이 0과 다른 3×3 행렬식을 가지므로 행렬 A의 순위는 3입니다.
![]()
A의 순위를 알고 나면 A’의 순위를 계산합니다. 이는 A’의 순위가 0과 다른 차수 3의 행렬식 내부에 있다는 것을 방금 확인했기 때문에 최소한 순위 3이 됩니다. 또한 순위 4가 될 수 없습니다. 4차 행렬식을 만들 수 없기 때문입니다. 따라서 행렬 A’도 랭크 3입니다.
![]()
따라서 행렬 A의 순위는 행렬 A’의 순위 및 시스템의 미지수 수(3)와 동일하므로 Rouché Frobenius의 정리를 통해 SCD( 호환성 결정 시스템 )임을 알 수 있습니다. :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
불확실한 호환 시스템(ICS)의 예
![Rendered by QuickLaTeX.com \begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2360b9a47257f73cf3f5dea63fb24098_l3.png)
시스템의 행렬 A 와 확장 행렬 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b281235e2702433b447e2586ae3092c9_l3.png)
이제 행렬 A의 순위를 계산합니다. 이를 위해 전체 행렬의 행렬식이 0과 다른지 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-74cafc27ab41134696c3bf263132b98b_l3.png)
전체 행렬 A의 행렬식은 0을 제공하므로 순위 3이 아닙니다. 순위 2인지 확인하려면 행렬식이 0과 다른 부분 행렬을 A에서 찾아야 합니다. 예를 들어 왼쪽 상단에서 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-22b2487f7664a70c116593120de2743b_l3.png)
행렬은 0과 다른 2×2 행렬식을 가지므로 행렬 A는 순위 2를 갖습니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 다른 가능한 3×3 행렬식을 시도해 봅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-17f264ad3859da88ffa6784be24e4143_l3.png)
행렬 A’의 모든 3×3 행렬식은 0이므로 행렬 A’도 순위 3이 아닙니다. 그러나 그 내부에는 0과 다른 차수 2의 결정자가 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-22b2487f7664a70c116593120de2743b_l3.png)
따라서 행렬 A’는 순위 2가 됩니다 .
![]()
행렬 A의 범위는 행렬 A’의 범위와 동일하지만 시스템의 미지수 수보다 적습니다(3). 따라서 Rouché-Frobenius 정리에 따르면 이는 불확정 호환 시스템 (ICS)입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
호환되지 않는 시스템(IS)의 예
![Rendered by QuickLaTeX.com \begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-30e1084dd637eb4371f6b2218af24136_l3.png)
시스템의 행렬 A 와 확장 행렬 A’는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b435d86f1466af5748d91e6c9bd813e3_l3.png)
이제 행렬 A의 순위를 계산합니다. 이를 위해 전체 행렬의 행렬식이 0과 다른지 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-714538c91aa2620a6adb40581245f0e0_l3.png)
전체 행렬 A의 행렬식은 0을 제공하므로 순위 3이 아닙니다. 순위 2인지 확인하려면 행렬식이 0과 다른 부분 행렬을 A에서 찾아야 합니다. 예를 들어 왼쪽 상단에서 :
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5a46decda8fd850d9c847922b0c896db_l3.png)
행렬이 0과 다른 2차 행렬식을 가지므로 행렬 A는 랭크 2입니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 이제 예를 들어 마지막 3개 열의 행렬식을 사용해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47aecdf801b92f21f2287fb96eaaa3f8_l3.png)
반면, 행렬 A’에는 결과가 0과 다른 행렬식이 포함되어 있으므로 행렬 A’는 순위 3을 갖습니다 .
![]()
따라서 행렬 A의 순위가 행렬 A’의 순위보다 작기 때문에 Rouché-Frobenius 정리에서 이것이 호환되지 않는 시스템 (SI)임을 추론합니다 .
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3da0513f318d25473e93ba88c51fb42_l3.png)
Rouché-Frobenius 정리의 문제 해결
연습 1
Rouché-Frobenius 정리를 사용하여 3개의 미지수가 있는 다음 방정식 시스템의 유형을 결정합니다.
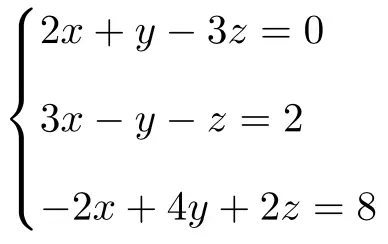
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-951ce5c1f0c606d4f060a1de58b60303_l3.png)
이제 행렬 A의 순위를 찾아야 합니다. 이를 위해 행렬의 행렬식이 0과 다른지 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-15cddb69f7590648d1d6ae61d942471e_l3.png)
0과 다른 3차 행렬식을 갖는 행렬인 행렬 A는 랭크 3을 갖습니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 이것은 적어도 랭크 3이 될 것입니다. 왜냐하면 우리는 내부에 0과 다른 차수 3의 행렬식이 있다는 것을 보았기 때문입니다. 또한 4×4 행렬식을 만들 수 없기 때문에 랭크 4가 될 수 없습니다. 따라서 행렬 A’도 랭크 3입니다.
![]()
따라서 Rouché-Frobenius 정리 덕분에 A의 범위는 A’의 범위 및 미지수의 개수와 동일하므로 이것이 확정 호환 시스템 (SCD)임을 알 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
연습 2
Rouché-Frobenius 정리를 사용하여 3개의 미지수가 있는 다음 방정식 시스템을 분류합니다.
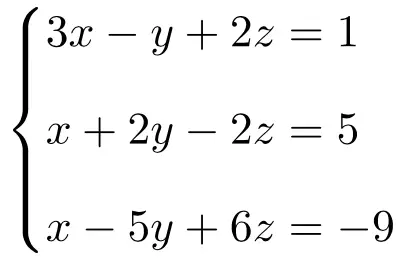
먼저 시스템의 행렬 A와 확장 행렬 A’를 구성합니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-45e13aabe233ece927df7c9ba0bb3ec1_l3.png)
이제 행렬 A의 범위를 계산해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-87bc95df0033834bba0398b8421faac5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9805283b75e2b89f67c7865a1263112_l3.png)
따라서 행렬 A에는 순위 2가 있습니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 다른 가능한 3×3 행렬식을 시도해 봅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6457fe3f03722b7f0d955191f318915_l3.png)
행렬 A’의 모든 3×3 행렬식은 0이므로 행렬 A’도 순위 3이 아닙니다. 그러나 그 내부에는 0과 다른 차수 2의 행렬식이 많이 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eafa4747802fae3f0c36350357abbeb2_l3.png)
따라서 행렬 A’는 순위 2가 됩니다 .
![]()
행렬 A의 순위는 행렬 A’의 순위와 동일하지만 이 두 가지는 시스템의 미지수 수(3)보다 적습니다. 따라서 Rouché-Frobenius 정리에 의해 우리는 이것이 불확정 호환 시스템 (ICS)임을 알 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
연습 3
다음 방정식 시스템이 Rouché-Frobenius 정리를 사용하는 시스템 유형을 결정합니다.
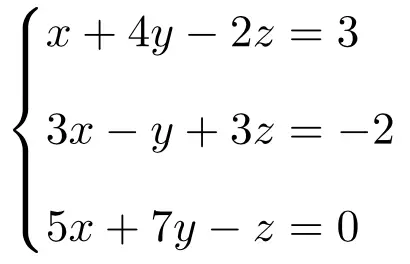
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1820d31e4fd5c79804c9b6fa15abb469_l3.png)
이제 행렬 A의 범위를 계산해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-4f998260ee4c96673085ea6fd4ca87ba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-159a1c58fdcd972b4b08e4795950e064_l3.png)
따라서 행렬 A에는 순위 2가 있습니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식은 0을 제공하지만 마지막 3개 열의 행렬식은 그렇지 않다는 것을 이미 알고 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c673a5bbbd41933208169fa3e08b7c62_l3.png)
따라서 행렬 A’는 랭크 3을 갖습니다 .
![]()
행렬 A의 순위는 행렬 A’의 순위보다 작으므로 Rouché-Frobenius 정리에서 이것이 호환되지 않는 시스템 (SI)임을 추론할 수 있습니다 .
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3da0513f318d25473e93ba88c51fb42_l3.png)
연습 4
Rouché-Frobenius 정리를 사용하여 3개의 미지수가 있는 다음 방정식 시스템의 유형을 결정합니다.
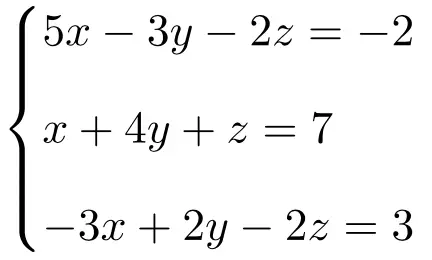
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8a0454c53a64f612c689ba1dae1196b_l3.png)
이제 행렬 A의 순위를 계산해야 합니다. 이를 위해 Sarrus 규칙을 사용하여 행렬의 행렬식을 해결합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-420f0d1ee000f39cbfbce88bf122f413_l3.png)
0과 다른 3차 행렬식을 갖는 행렬인 행렬 A는 랭크 3을 갖습니다.
![]()
따라서 행렬 A’는 항상 순위 A 이상이므로 순위 3이기도 하며 , 4×4 행렬식을 해결할 수 없기 때문에 순위 4가 될 수 없습니다.
![]()
따라서 Rouché-Frobenius 정리의 적용 덕분에 A의 범위가 A’의 범위 및 미지수의 개수와 동일하기 때문에 시스템이 호환 가능 시스템 (SCD)임을 알 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
연습 5
다음 방정식 시스템이 Rouché-Frobenius 정리를 사용하는 시스템 유형을 식별합니다.
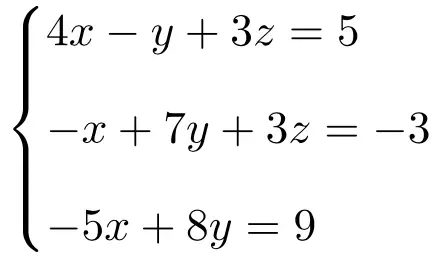
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3211e276b2b040969c38bc6c69eabd52_l3.png)
이제 행렬 A의 범위를 계산해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-21004095a3a8ef3edfc15bed5c7853a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a58059046b56cf1f8d82c6c8939e44ca_l3.png)
따라서 행렬 A는 순위 2입니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리가 이미 알고 있는 처음 3개 열의 행렬식은 0을 제공하지만 마지막 3개 열의 행렬식은 다음을 제공하지 않습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-992718d3b50aedf77c80c262fad5845f_l3.png)
따라서 행렬 A’는 랭크 3을 갖습니다 .
![]()
그리고 마지막으로 도메인을 Rouché-Frobenius 정리에 적용합니다. 행렬 A의 도메인은 행렬 A’의 도메인보다 작으므로 호환되지 않는 시스템 (SI)입니다 .
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3da0513f318d25473e93ba88c51fb42_l3.png)
연습 6
Rouché-Frobenius 정리를 사용하여 다음 3차 방정식 시스템을 분류합니다.
![Rendered by QuickLaTeX.com \begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d45e8bc425b08e403a98e01693201681_l3.png)
먼저 시스템의 행렬 A와 확장 행렬 A’를 구성합니다.
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e779eca9135adc44e4a3a55f368560f_l3.png)
이제 행렬 A의 범위를 계산해 보겠습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2f63f79858eae462547cf2f270fc780_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5fa293b94b8c6acfd998f1e154abf7a_l3.png)
따라서 행렬 A에는 순위 2가 있습니다.
![]()
A의 순위를 알면 A’의 순위를 계산합니다. 우리는 처음 3개 열의 행렬식이 0이라는 것을 이미 알고 있으므로 다른 가능한 3×3 행렬식을 시도해 봅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-98958f866454a1bf9f1ac078562065cd_l3.png)
행렬 A’의 모든 3×3 행렬식은 0이므로 행렬 A’도 순위 3이 아닙니다. 그러나 그 내부에는 0과 다른 차수 2의 결정자가 있습니다. 예를 들면 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-58091f1a37a4ef81fdf56f01dd9531a3_l3.png)
따라서 행렬 A’는 순위 2가 됩니다 .
![]()
마지막으로 Rouché-Frobenius 정리를 적용하여 행렬 A의 범위가 행렬 A’의 범위와 동일하지만 이 두 개가 행렬의 미지수 수보다 작기 때문에 이것이 불확정 호환 시스템 (ICS)이라는 것을 알 수 있습니다. 시스템(3):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)