이 페이지에서는 나선형 행렬이 무엇인지 배우게 됩니다. 또한 2×2, 3×3, 4×4 차원의 포함 행렬의 예를 보여줍니다. 그리고 마지막으로, 회전 행렬의 공식을 찾을 수 있습니다.
회전 행렬이란 무엇입니까?
회전 행렬의 의미는 다음과 같습니다.
포함행렬의 정의 : 역행렬이 행렬 그 자체인 가역정사각행렬.
![]()
금
![]()
임의의 행렬이고
![]()
그 반대를 나타냅니다.
따라서 분명히 회전 행렬은 일반 또는 비축퇴 행렬의 예 입니다.
역행렬이 무엇인지 모르는 경우 여기에서 3×3 역행렬을 계산하는 방법을 볼 수 있습니다. 행렬을 반전시키는 방법을 아는 것이 중요합니다. 그러나 이를 위해서는 행렬의 수반이 계산되는 방법도 알아야 합니다.
그러나 다시 주제로 돌아가서, 행렬이 포함된 경우 행렬 자체에 행렬을 곱하면 단위 행렬이 됩니다. 데모를 살펴보세요:
역행렬을 곱한 행렬은 항등(또는 단위) 행렬을 제공합니다. 그래서:
![]()
그리고 회전 행렬의 역행렬은 행렬 자체이기 때문에:
![]()
결과적으로 제곱된 혁명 행렬은 단위 행렬을 제공합니다.
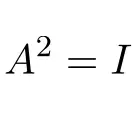
회전 행렬의 예
2×2 인볼루션 행렬의 예:
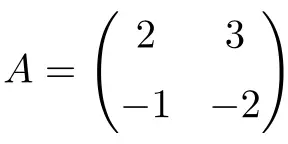
행렬의 2차 거듭제곱을 계산하여 이것이 회전 행렬임을 확인할 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-314aebadfe3da501264c0eb14e1dfc2f_l3.png)
행렬 A의 제곱은 단위 행렬이므로 행렬 A는 2×2 회전 행렬입니다.
3×3 인볼루션 행렬의 예:
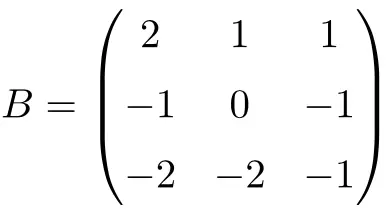
행렬의 곱을 그 자체로 풀어서 이것이 회전 행렬임을 확인할 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599241f00e8a89f8b55ed2ae8cb42ddb_l3.png)
행렬 B의 제곱은 단위 행렬이므로 행렬 B는 3×3 회전 행렬입니다.
4×4 인볼루션 행렬의 예:
항등(또는 단위) 행렬은 차원에 관계없이 정의에 따라 회선 행렬입니다.
![Rendered by QuickLaTeX.com \displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4278c2b46761d3b258eb9ba04c87bbf1_l3.png)
행렬을 2로 올려서 이것이 회전 행렬임을 확인할 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3190f24d196c4b96a60ec06fe7180e6_l3.png)
제곱 단위 행렬은 단위 행렬이므로 단위 행렬은 4×4 회전 행렬이다.
분명히 단위 행렬은 주대각선이 모두 1이고 나머지가 0인 단순한 대각 행렬이기 때문에 모든 차원이 될 수 있습니다. 따라서 단위 행렬은 순서에 관계없이 항상 역행렬이 됩니다.
복잡한 행렬 공식
회전 행렬의 특성 중 하나는 공식을 알 수 있다는 것입니다. 하지만 2차 진화 행렬에 대한 공식의 증명은 꽤 지루하므로 결과를 바로 알려드리겠습니다. 이것이 정말 중요합니다. 데모에 더 관심이 있으시면 아래 댓글에서 단계별로 설명된 내용을 확인하실 수 있습니다.
차원 2 × 2의 포함 행렬에 대한 공식은 다음과 같습니다.

따라서 주대각선 값이 반대이고 행렬식이 -1인 모든 행렬은 회전 행렬이 됩니다.
그러나 이 공식으로 설명되는 행렬 외에도 단위 행렬과 그 반대 행렬도 2차 회전 행렬이라는 점을 고려해야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-395beb5a766a10eefa56a087e8c8d098_l3.png)
나선형 행렬의 속성
회전 행렬은 다음과 같은 특징을 가지고 있습니다.
- 회전 행렬의 행렬식은 항상 -1 또는 +1과 같습니다.
- 회생 행렬과 멱등 행렬 사이에는 다음과 같은 관계가 있습니다 .

행렬이 다음과 같은 경우에만 혁명적입니다.
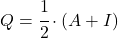
멱등성이다.
- 응

그리고

두 개의 통근 혁명적 행렬이면 행렬 곱은 다음과 같습니다.
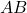
또 다른 혁명적 행렬입니다.
- 회생 행렬의 모든 거듭제곱은 또 다른 회연 행렬을 생성합니다. 특히, 홀수 지수로 상승한 나선형 행렬은 그 자체와 동일하며, 반면에 짝수 지수로 상승하면 항등 행렬과 동일합니다.
![]()
![]()