유리함수: 정의역, 점근선, 그래프, 연습 문제,...

여기에서 유리함수(rational function)가 무엇인지 알게 될 것입니다. 추가적으로, 유리함수의 정의역과 점근선을 계산하는 방법을 설명합니다. 그뿐만 아니라 유리함수의 모든 특징이 무엇인지 알게 될 것입니다. 마지막으로 유리함수에 대한 단계별 연습을 통해 연습할 수 있습니다.

유리함수란 무엇인가?

유리함수의 정의는 다음과 같습니다.

유리함수는 두 다항식의 몫으로 구성된 함수 , 즉 유리함수는 분자와 분모에 다항식이 있는 분수입니다.

유리함수는 분모가 사라지는 지점의 특이점을 특징으로 합니다.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

유리수 함수는 분수 함수라고도 합니다.

반면에, 유리함수는 비합리적 함수와 혼동되어서는 안 됩니다. 비합리적(또는 급진적) 함수는 근으로 구성된 함수입니다.

유리 함수의 예

유리함수의 개념을 더 잘 이해하기 위해 이러한 유형의 함수에 대한 몇 가지 예를 살펴보겠습니다.

분자와 분모에 1차 다항식이 있는 유리 함수:

$f(x)=\cfrac{x+3}{2x-5}$

이러한 유형의 유리 함수를 동형 함수 라고도 합니다.

분자에 상수가 있고 분모에 다항식이 있는 유리 함수:

$f(x)=\cfrac{7}{x+1}$

이러한 유형의 유리 함수를 역비례 함수 라고 하며 반비례 수량을 수학적으로 정의하는 데 사용됩니다.

분자에 3차 다항식이 있고 분모에 2차 다항식이 있는 유리 함수:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

유리함수의 영역

0으로 나눈 숫자는 무한대(무한대)를 제공하는 불확정성이므로 분모가 0이 아닌 한 유리 함수는 항상 존재합니다.

따라서 유리함수의 정의역은 분모를 상쇄하는 값을 제외한 모든 실수로 구성됩니다.

따라서 유리 함수의 정의역을 얻으려면 분모가 0일 때를 찾아야 합니다. 왜냐하면 이 점은 정의역에 속하지 않는 유일한 점이기 때문입니다.

예제를 풀어 유리 함수의 정의역이 어떻게 계산되는지 살펴보겠습니다.

$f(x)=\cfrac{5x}{x+2}$

먼저 분모를 0으로 설정한 다음 결과 방정식을 풉니다.

$x+2=0$

$x=-2$

따라서 x가 -2이면 분모는 0이 되고 따라서 함수는 존재하지 않습니다. 따라서 함수의 정의역은 x=-2를 제외한 모든 실수로 구성됩니다. 이는 다음과 같이 명시됩니다.

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

유리 함수의 점근선

유리 함수의 주요 속성 중 하나는 점근선입니다. 점근선이 그래픽 표현을 결정하기 때문입니다.

➤ 참조: 기능의 그래픽 표현

유리 함수의 점근선은 함수 그래프가 무한정 접근하지만 결코 닿지 않는 선입니다.

점근선에는 세 가지 유형이 있습니다: 수직 점근선, 수평 점근선, 경사 점근선.

아래에는 유리 함수가 빨간색으로 그래프로 표시할 수 있는 세 가지 유형의 점근선이 있습니다.

유리 함수의 수직 점근선

유리 함수의 수평 점근선

유리 함수의 경사 점근선

보시다시피, 그래프에서 함수의 점근선을 결정하는 것은 매우 간단하지만 그래프 표현 없이 유리 함수의 점근선을 계산하는 것은 매우 복잡합니다. 이것이 바로 우리 웹사이트에서 함수의 점근선이 어떻게 계산되는지 확인하는 것을 권장하는 이유입니다.

유리함수의 특징

유리수 함수에는 다음과 같은 특징이 있습니다.

$f(x)=\cfrac{P(x)}{Q(x)}$

위에서 본 것처럼 유리함수의 영역에는 분수의 분모를 상쇄하는 값을 제외한 모든 실수가 포함됩니다.

일반적으로 유리함수의 범위(또는 범위)에는 함수가 수평 점근선을 갖는 값을 제외한 모든 실수가 포함됩니다.

합리적 기능은 해당 영역 전체에서 연속적입니다. 즉, 유리함수는 자신의 영역에 속하지 않는 점에서 불연속성을 나타냅니다.

대부분의 유리 함수의 그래픽 표현은 두 개의 쌍곡선으로 구성됩니다.

유리 함수의 점근선에 대한 일부 규칙은 다항식 분자로부터 추론될 수 있습니다.
$P(x)$

그리고 분모 다항식

$Q(x):$
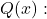
- 유리함수는 다음의 근이 되는 점에 수직 점근선을 갖습니다.
  $Q(x)$
  
  하지만 이것들은 뿌리가 아니다.
  
  $P(x).$
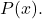
- 정도라면
  $P(x)$
  
  정도 미만이다.
  
  $Q(x)$
  
  , y=0 선은 유리 함수의 수평 점근선입니다.
- 정도라면
  $P(x)$
  
  정도보다 크다
  
  $Q(x)$
  
  , 유리 함수에는 수평 점근선이 없습니다.
- 정도라면
  $P(x)$
  
  정도보다 큰 단위이다.
  
  $Q(x)$
  
  그리고 두 다항식은 공통 근을 가지지 않으며, 유리 함수는 경사 점근선을 갖습니다.

합리적인 함수에 대한 해결 연습

연습 1

다음 유리 함수의 정의역을 찾으세요:

$f(x)=\displaystyle\frac{4x}{2x+4}$

솔루션 보기

이것은 유리함수이므로 정의역은 분모를 취소하는 숫자를 제외한 모든 숫자로 구성됩니다. 왜냐하면 이 함수는 무한대를 제공하기 때문입니다.

따라서 어떤 숫자가 도메인에 속하지 않는지 확인하기 위해 정수 분모를 0으로 설정합니다.

$2x+4=0$

그리고 우리는 결과 방정식을 푼다:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

따라서 함수의 정의역은 -2를 제외한 숫자로만 구성됩니다.

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

연습 2

데카르트 축을 사용하여 다음 유리 함수의 컷오프 지점을 찾습니다.

$f(x)=\cfrac{x^2-9}{x}$

솔루션 보기

X축 절단점

함수와 X축의 교차점을 찾으려면 다음을 풀어야 합니다.

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

우리는 이차 방정식의 두 가지 해를 얻었으므로 유리 함수는 다음과 같은 두 가지 다른 지점에서 가로축과 교차합니다.

$\bm{(3,0)\qquad (-3,0)}$

Y축을 사용한 절단점

Y축과의 교차점을 찾으려면 다음을 계산해야 합니다.

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

0으로 나눈 모든 숫자는 무한대를 제공하는 불확정성입니다. 따라서 유리함수는 Y축 위의 어떤 지점도 통과하지 않습니다. 즉, y축과 교차하는 지점이 없습니다.

연습 3

다음 유리함수를 그래프에 그려보세요:

$y=\cfrac{2x+3}{2x+6}$

솔루션 보기

가장 먼저 해야 할 일은 함수의 정의역을 계산하는 것입니다.

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

함수의 영역을 알고 나면 값 테이블을 구성합니다.

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

마치려면 그래프에서 얻은 점을 간단히 표현하고 쌍곡선을 그려 유리 함수를 그립니다.

연습 4

아래 그래프에 표시된 유리 함수의 점근선을 결정합니다.

솔루션 보기

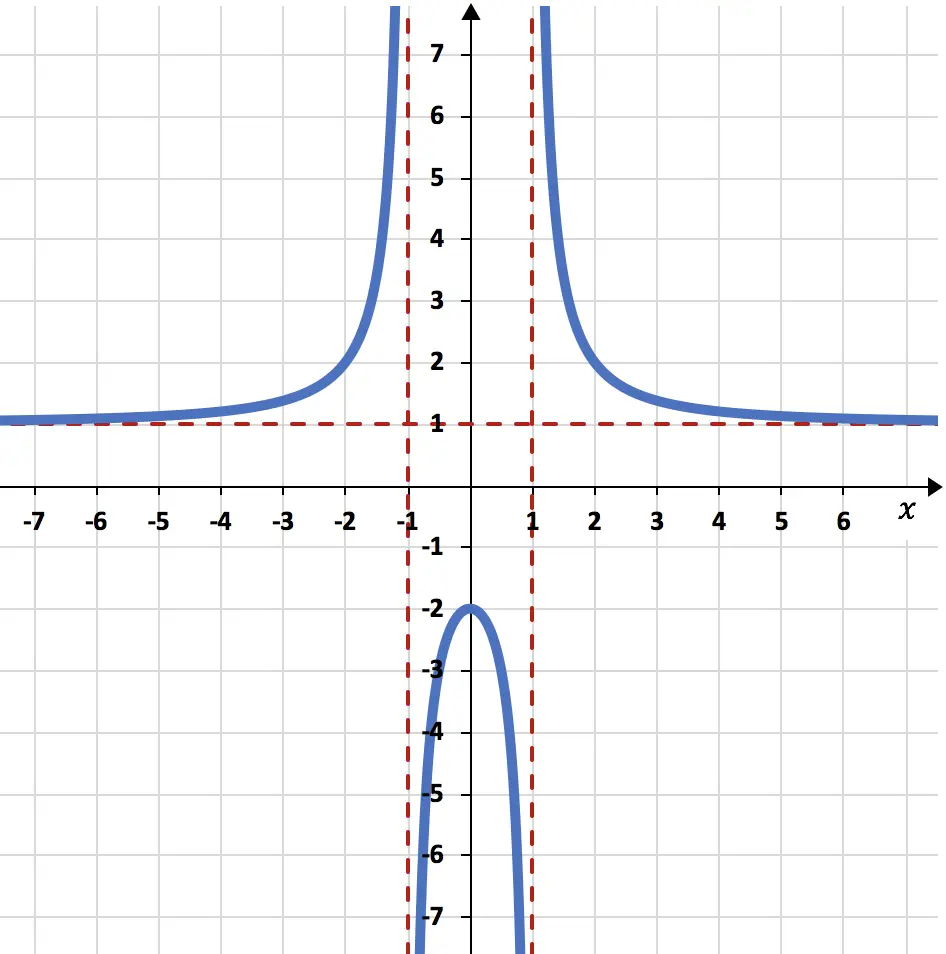
점근선은 빨간색 점선으로 표시되므로 그래프에서 매우 명확하게 표시됩니다.

이 문제에서 함수는 수평선 y=1에 매우 가깝지만 결코 닿지 않습니다. 따라서 유리 함수는 y=1인 단일 수평 점근선을 갖습니다.

마찬가지로 함수의 그래픽 표현은 수직선 x=-1 및 x=1에 매우 가깝지만 이러한 값에는 도달하지 않습니다. 따라서 유리 함수는 두 개의 서로 다른 수직 점근선, 즉 x=-1과 x=1을 갖습니다.

연습 5

다음 유리 함수의 모든 점근선을 계산합니다.

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

참고: 이 연습 문제를 해결하려면 먼저 함수의 점근선 계산 방법에 대한 위의 링크로 이동하여 설명을 확인하는 것이 좋습니다.

솔루션 보기

수직 점근선

함수의 수직 점근선을 계산하려면 먼저 함수의 정의역을 찾아야 합니다. 따라서 우리는 정의역에 속하지 않는 점을 찾기 위해 유리함수의 분모를 0으로 설정합니다.

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

따라서 함수의 정의역은 -1을 제외한 모든 숫자로 구성됩니다.

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

따라서 x=-1은 수직 점근선이 될 수 있습니다. 이를 확인하려면 해당 지점에서 함수의 극한을 계산해야 합니다.

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

따라서 x=-1은 유리 함수의 수직 점근선입니다. 왜냐하면 이 지점에서 함수의 극한이 무한대를 제공하기 때문입니다.

수평 점근선

수평 점근선을 결정하려면 함수의 무한 극한을 계산해야 합니다.

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

이 경우, 무한대 사이의 불확실한 무한 극한의 결과는 분자와 분모가 동일한 차수이기 때문에 최고 차수 x의 계수를 나누는 것입니다.

함수의 두 무한 극한은 3을 주므로 y=3은 유리 함수의 수평 점근선입니다.

경사 점근선

수평 점근선이 있기 때문에 유리 함수에는 경사 점근선이 없습니다.

유리함수란 무엇인가?

유리 함수의 예

유리함수의 영역

유리 함수의 점근선

유리함수의 특징

합리적인 함수에 대한 해결 연습

연습 1

연습 2

연습 3

연습 4

연습 5

댓글 달기 댓글 취소